Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 399
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
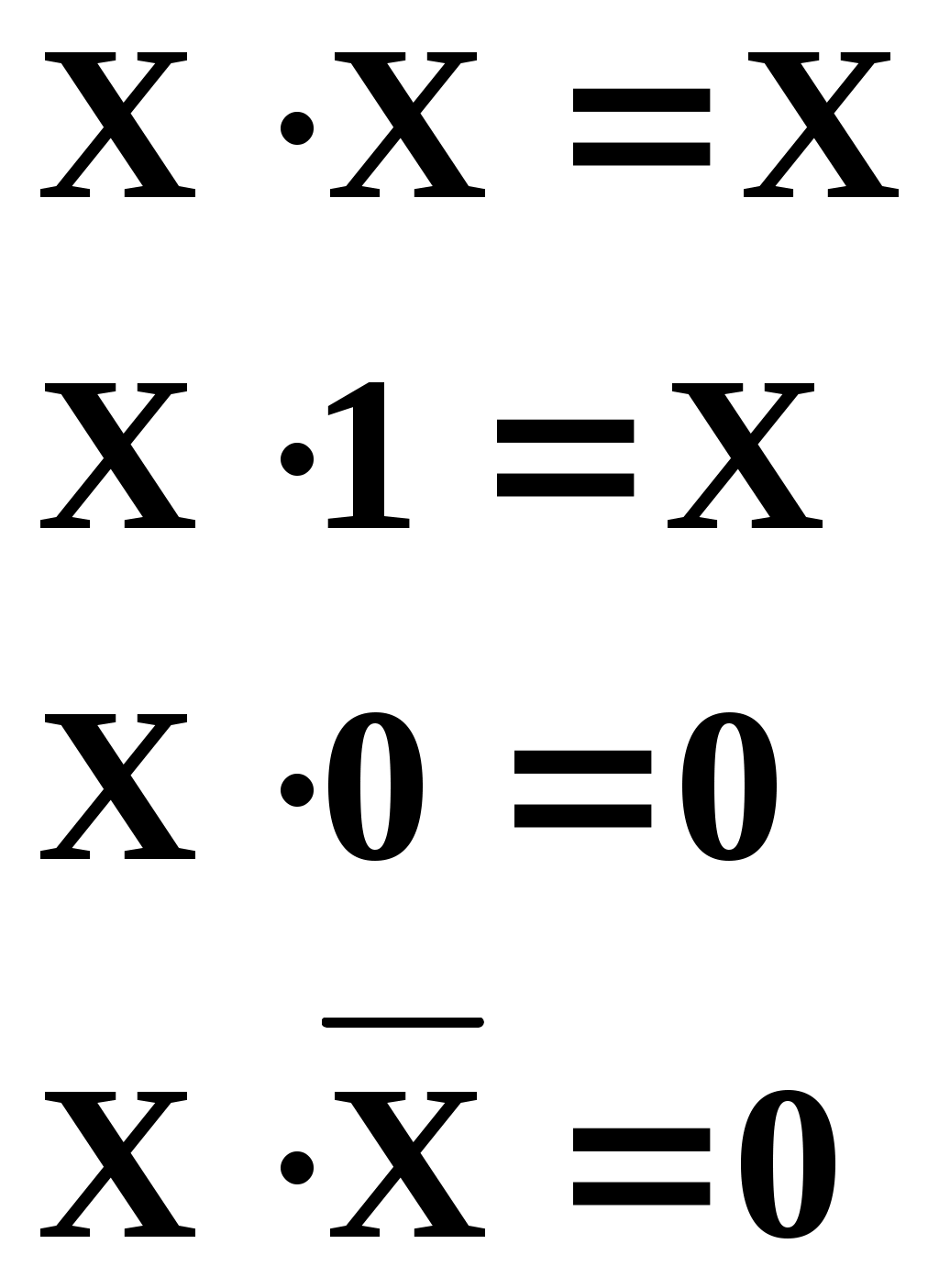
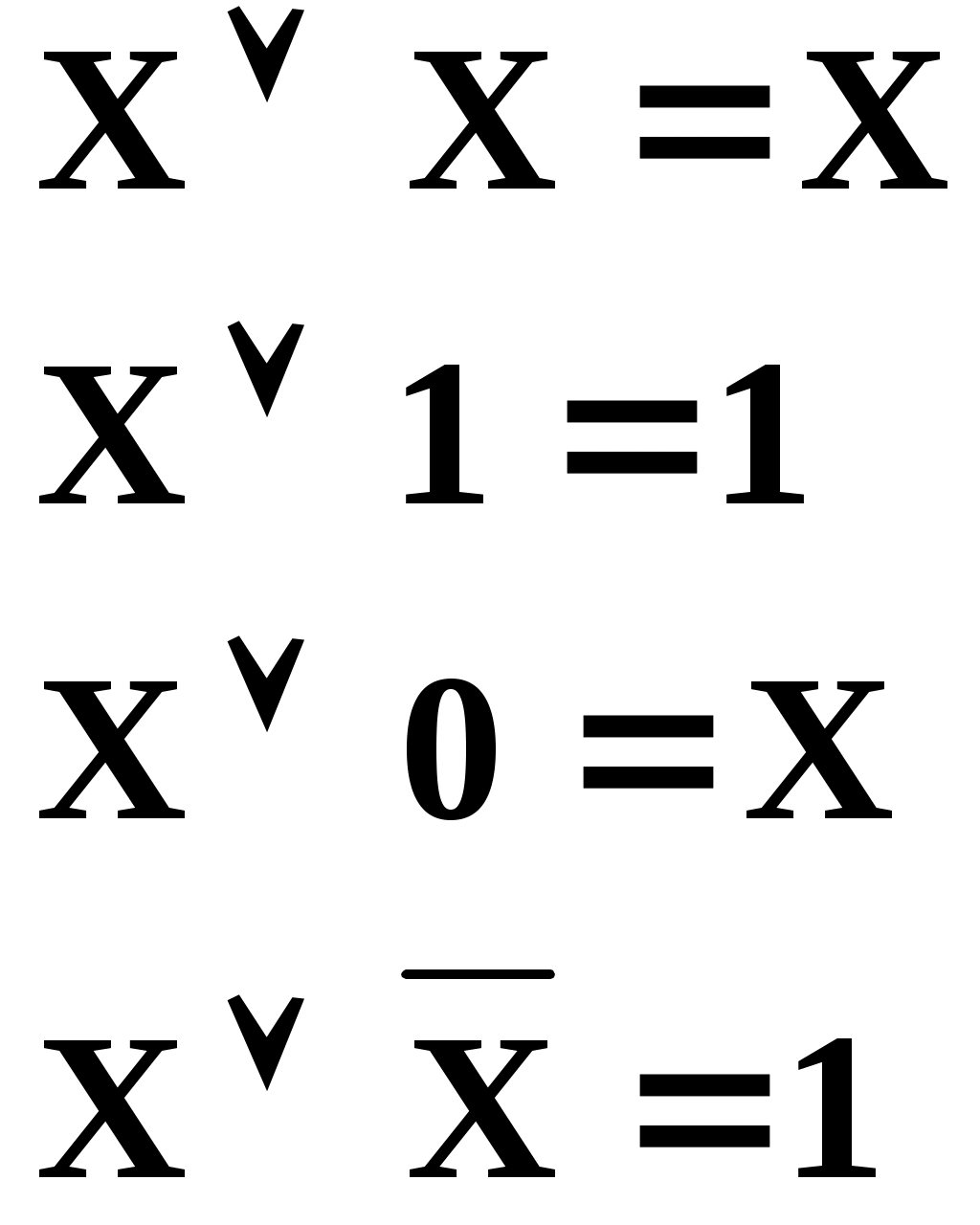
Убедиться в справедливости приведенных тождеств можно путем подстановки значений аргумента Х, равных 0 или 1.
Сравнивая формулы основных тождеств можно утверждать, что между ними существует взаимосвязь. Она заключается в следующем:
Действие «ИЛИ» можно заменить действием «И» (и наоборот), при этом необходимо инвертировать каждую логическую величину, входящую в формулу.
То есть: для конъюнкции для дизъюнкции
Это свойство логических действий получило название свойство двойственности.
Докажем это свойство:
для конъюнкции для дизъюнкции
(логического умножения) (логического сложения)
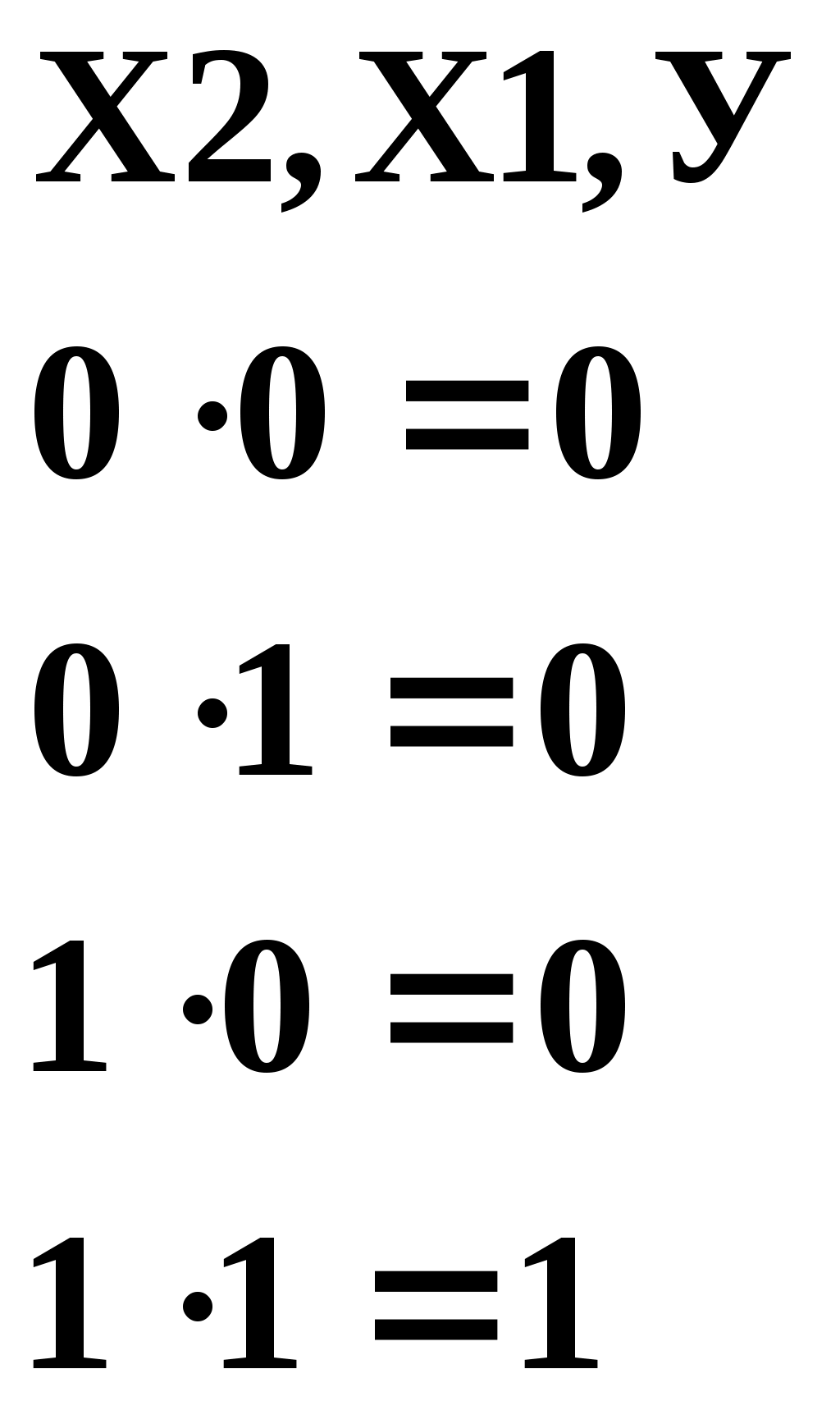

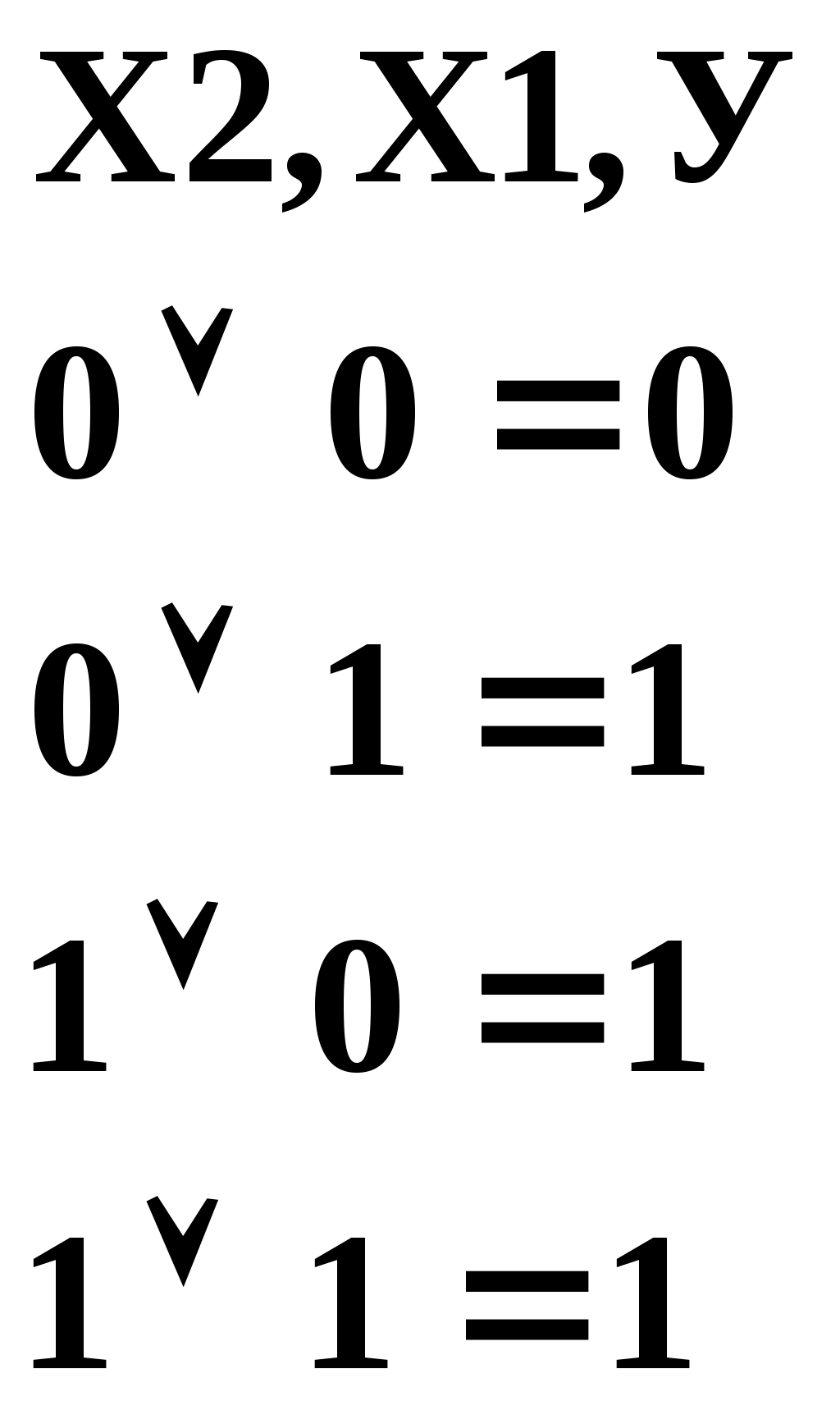
Воспользуемся свойством двойственности и сравним логические выражения.
Для конъюнкции:
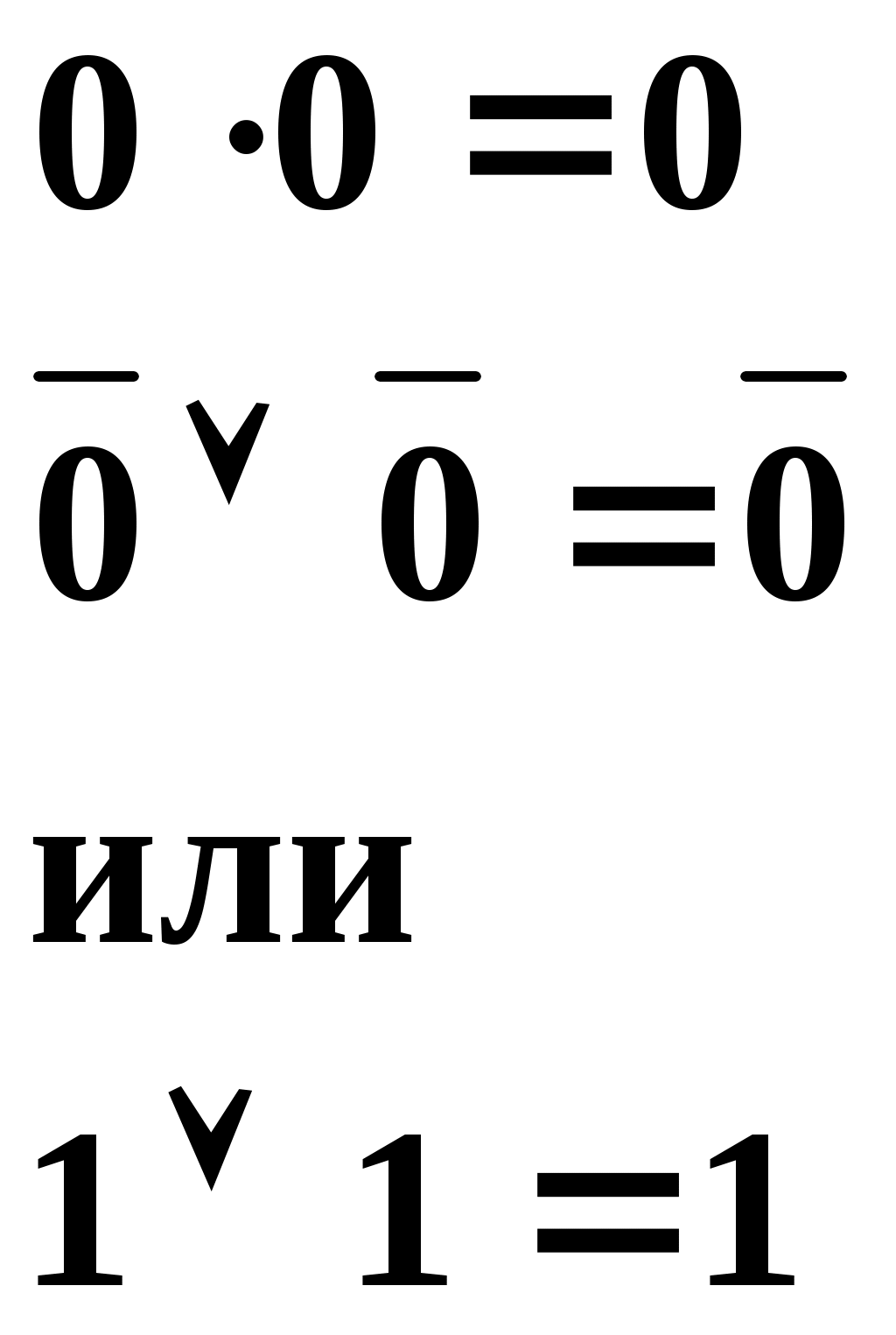
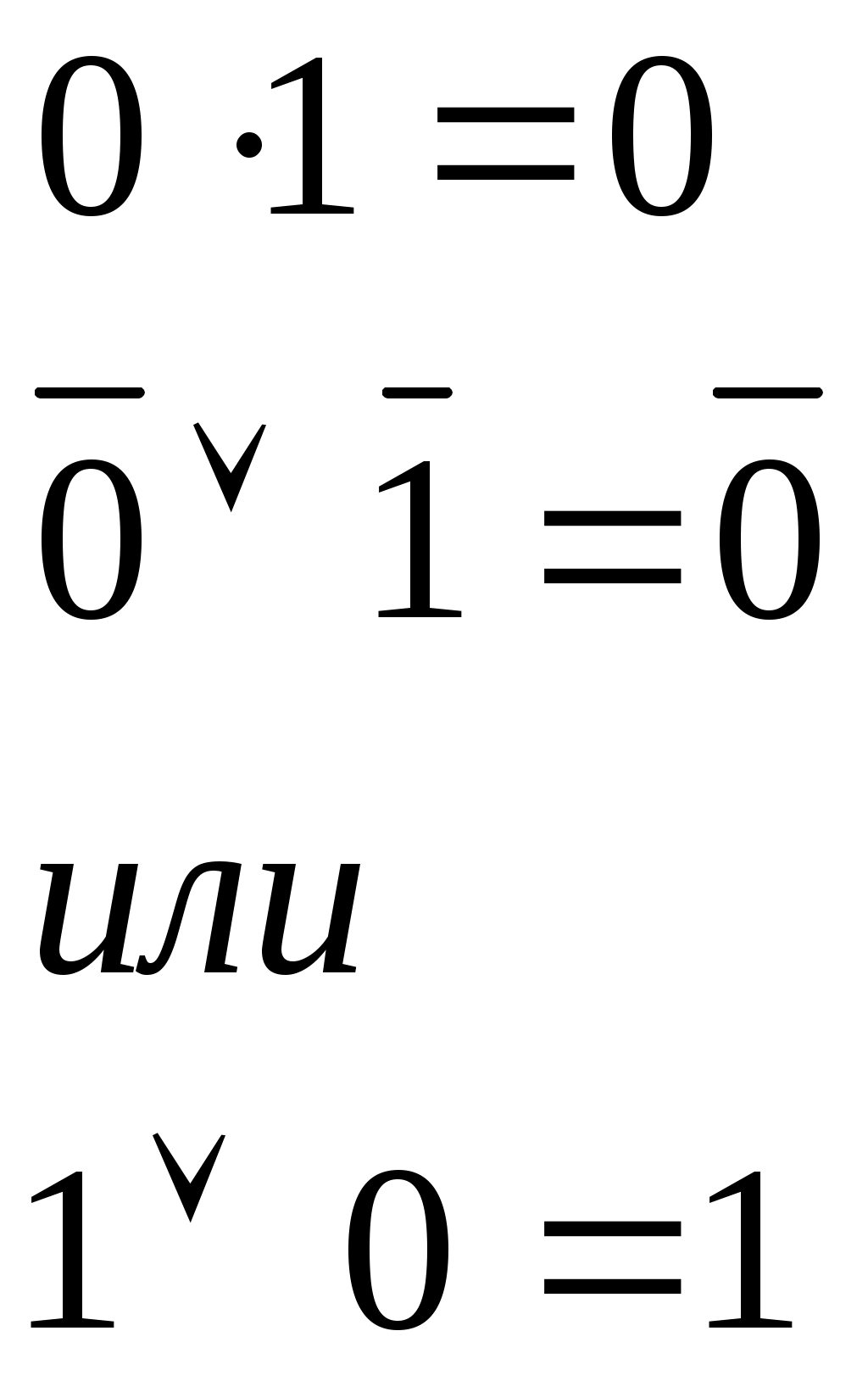
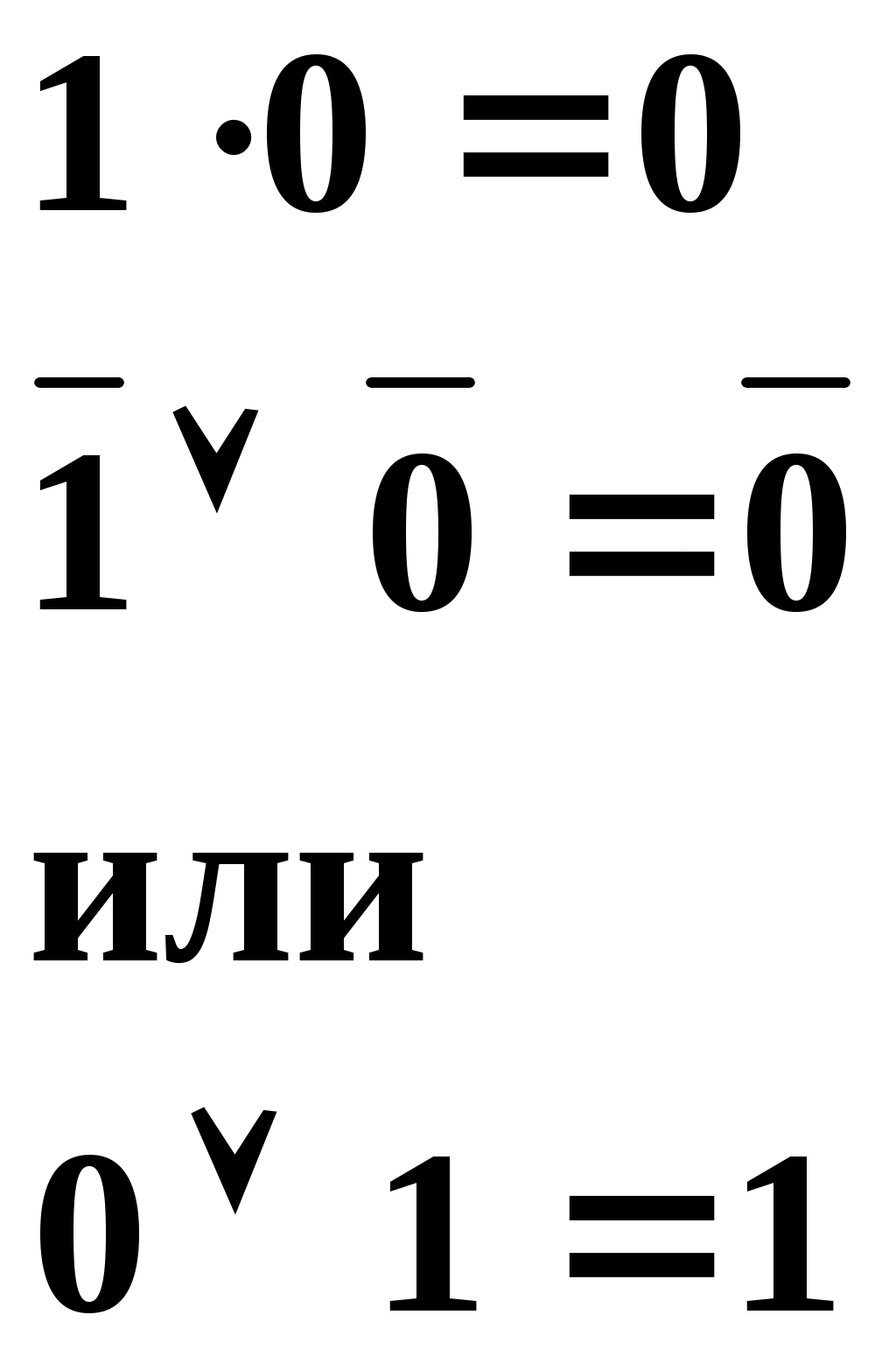
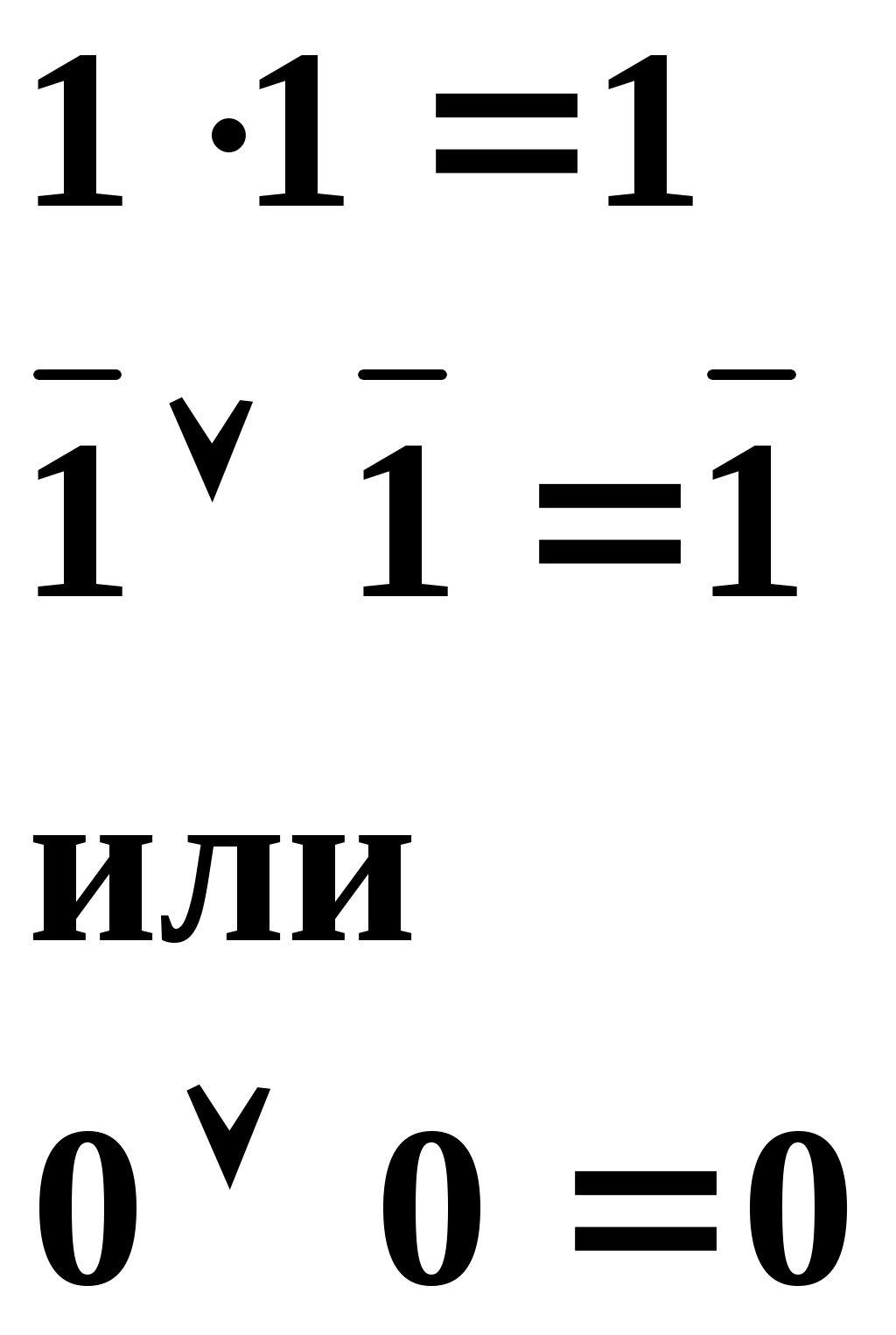
Данную взаимосвязь имеют и логические выражения для конъюнкции. Пунктирными стрелками указаны пары таких логических выражений. В них на основании свойства двойственности «0» переходит в «1», а «1» переходит в «0». Знаки конъюнкции (●)и дизъюнкции (
0→1, 1→0, (●)→(
Кроме свойства двойственности существует свойство сохранения нуля, которое заключается в том, что каждая функция может иметь только одно уравнение, записанное в форме СНКФ.
Свойство сохранения единицы
заключается в том, что каждая функция может иметь только одно уравнение, записанное в форме СНДФ.
* Основные законы:
-
Переместительный
Для дизъюнкции
Для конъюнкции
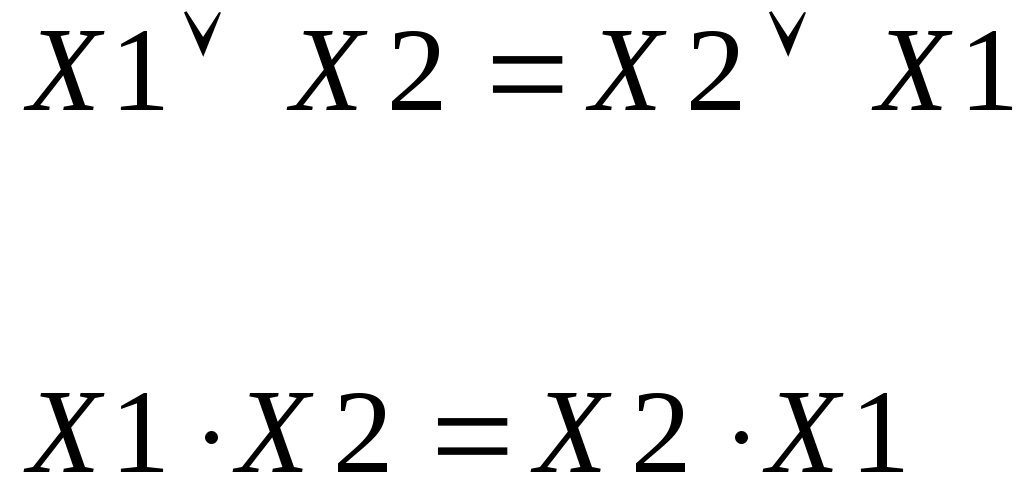
Этот закон указывает, что от перестановки мест аргументов значение функции не изменится.
2 Сочетательный
Для дизъюнкции
Для конъюнкции
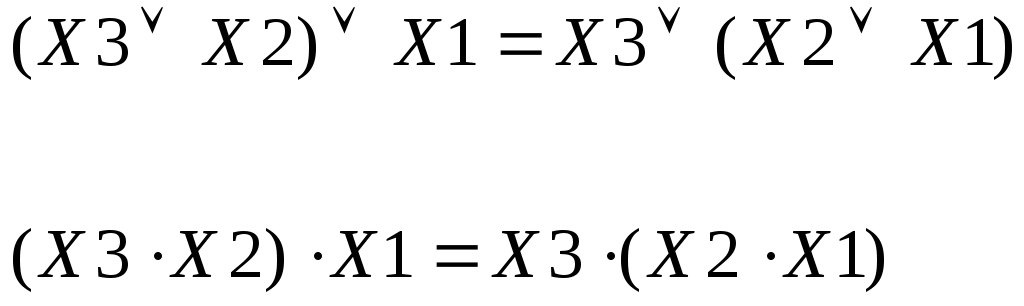
Данный закон позволяет образовать сумму или произведение любой комбинации аргументов.
-
Распределительный
Для дизъюнкции
Для конъюнкции
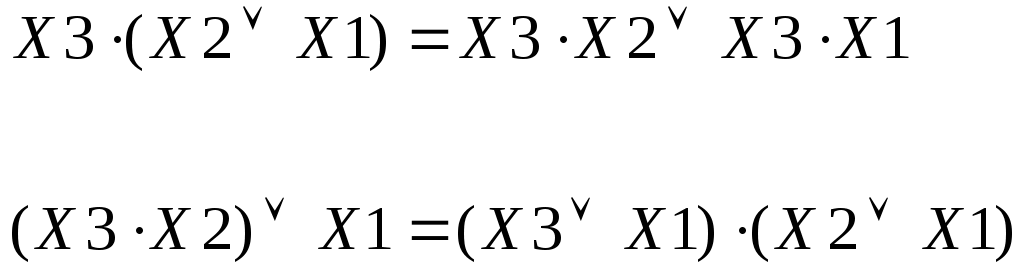
Распределительный закон позволяет получить попарно дизъюнкцию двух конъюнкций или конъюнкцию двух дизъюнкций.
Приведенные законы алгебры логики идентичны соответствующим законам общей алгебры, за исключением распределительного закона для конъюнкции (последнее выражение).
4 Закон двойного отрицания
Если Х=1, то
Закон двойного отрицания утверждает, что двойное отрицание аргумента есть сам аргумент.
* Теоремы:
Теоремы доказываются с помощью применения законов алгебра логики и свойств конъюнкции и дизъюнкции.
Теорема Моргана:
Теорема Моргана показывает, что:
1 Отрицание дизъюнкции аргументов равно конъюнкции отрицаний этих аргументов;
-
Отрицание конъюнкции аргументов равно дизъюнкции отрицаний этих аргументов.
Теорема Моргана доказывается на основании свойства двойственности:
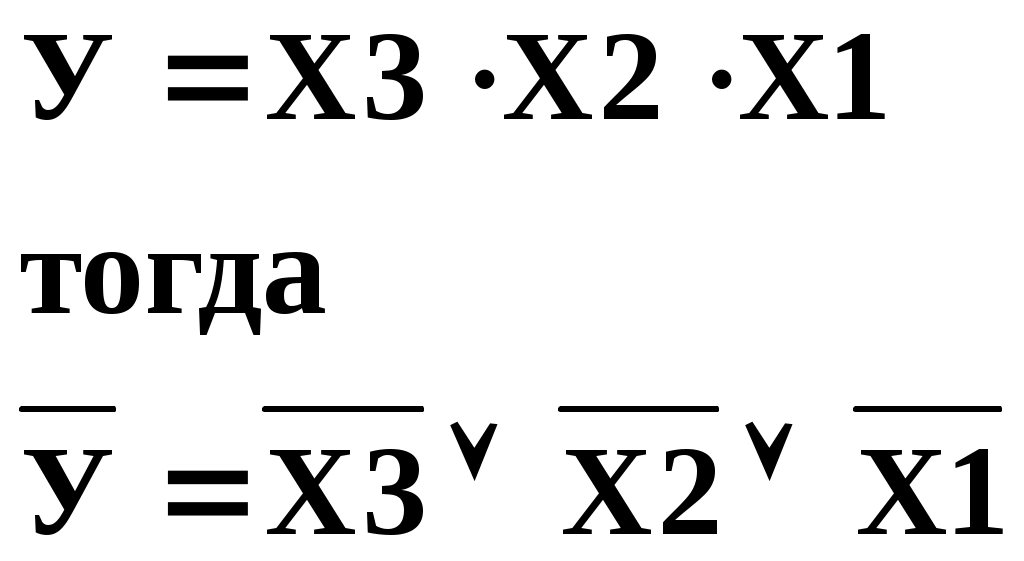
Под знак инверсии вместо У подставляем его значение. Таким образом,
и на основании свойства двойственности получаем, что:
По такому же принципу доказывается теорема Моргана для дизъюнкции.
Теорема поглощения:
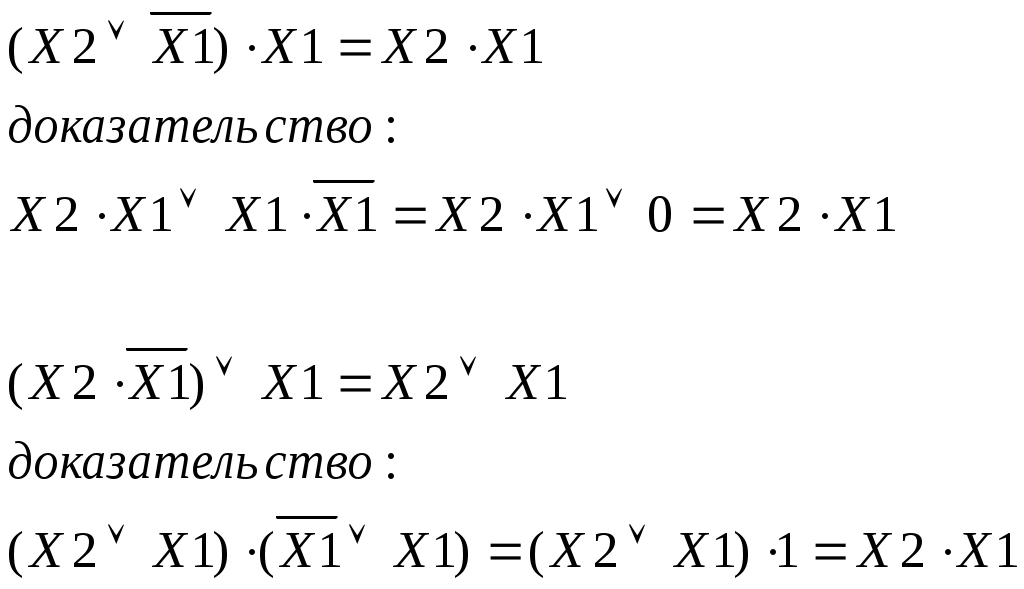
Теорема склеивания:
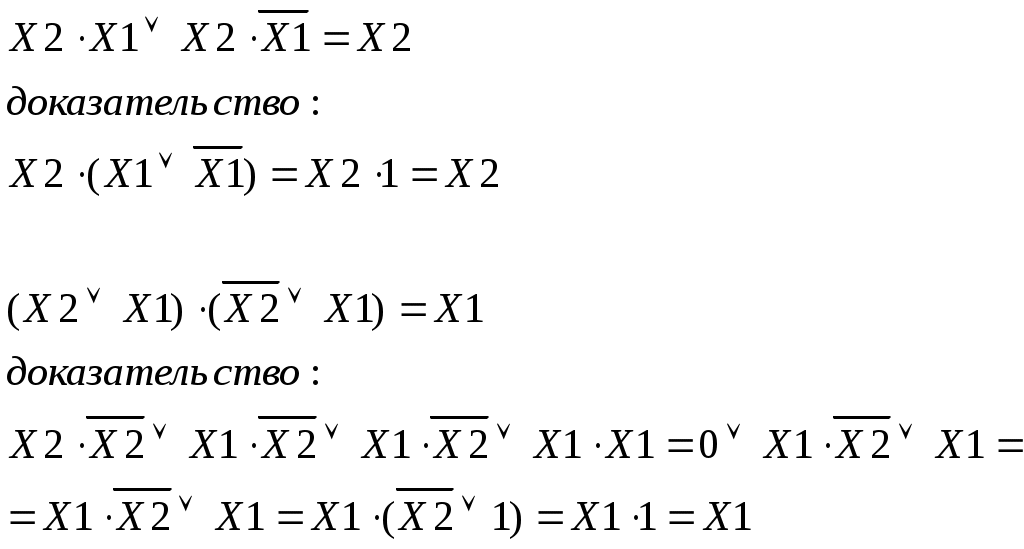
При упрощении логических функций следует учитывать очередность выполнения логических операций:
-
Инверсия -
Конъюнкция -
Дизъюнкция.
Однако при наличии скобок в логическом выражении эта очередность может измениться.
1.2.5 Понятие о функционально полных системах (ФПС) логических функций (базиса)
* Определение ФПС. Примеры минимальных базисов
Используя набор простейших логических элементов можно построить любую логическую схему по заданному логическому выражению (функции).
Система элементов, позволяющая строить на их базе логическую схему любой сложности называется функционально полной системой элементов или базисом.
С помощью логической операции конъюнкции (И), дизъюнкции (ИЛИ) и инверсии (НЕ) можно записать любую другую из элементарных функций f0 …f15 . Любая логическая функция, как бы сложна она не была, может быть представлена через эти логические операции. Таким образом, этот набор элементов является функционально полной системой.
Существуют различные базисы и минимальные базисы, отличающиеся друг от друга числом входящих в них логических функций и элементов.
Самыми распространенными базисами, используемыми при синтезе устройств являются :
-
базис И, ИЛИ, НЕ -
базис И-НЕ -
базис ИЛИ-НЕ
* Базис «И, ИЛИ, НЕ»
Базис И, ИЛИ, НЕ обычно используется при начальной стадии проектирования устройств для построения функциональной схемы. Практически для реализации устройств обычно используется базис И—НЕ либо ИЛИ—НЕ. Элементы этого базиса широко выпускаются промышленностью в интегральном исполнении.
1.2.6 Преобразование логических функций из основного базиса в неосновные
Возможен переход от одного вида базиса к другому. Для перехода необходимо воспользоваться законом двойного отрицания и теоремой Моргана. В некоторых случаях достаточно применить знак инверсии с обеих частей равенства.
то есть:
По такому же принципу используется теорема Моргана для дизъюнкции трех аргументов и более:
Логические схемы ЦУ после такого преобразования содержат только элементы И—НЕ либо ИЛИ—НЕ. Функция НЕ в таких схемах не используется.
* Базис «И-НЕ»
Для реализации функции НЕ через базис И—НЕ необходимо воспользоваться основными тождествами алгебры логики. На основании этого:
Для представления функции И через элемент И—НЕ воспользуемся законом двойного отрицания:
Полученное значение функции является инверсной. На основании примера инверсию можно представить как:
Реализации функции ИЛИ через базис И—НЕ. Применяем теорему Моргана:
На рисунке 1 приведен способ реализации инвертора (функция НЕ -- рисунок 1а) в базисе И—НЕ (рисунок 1б) и ИЛИ—НЕ (рисунок 1в).

Х
Х
Х

а)
в)
Рисунок 14 – Реализация функции НЕ 1а) через функцию И—НЕ 1б) через функцию ИЛИ--НЕ 1в)
Рассмотрим еще один способ перевода в базис без применения инверторов.
Для перехода к элементам И-НЕ в правой части МНДФ применяем закон двойного отрицания и затем преобразуем на основе т. Моргана
После такого преобразования в структурной схеме потребуются логические элементы типа И-НЕ и НЕ. Так как нам необходимо построить схему без применения инверторов, выполним дальнейшее преобразования с использованием формул:
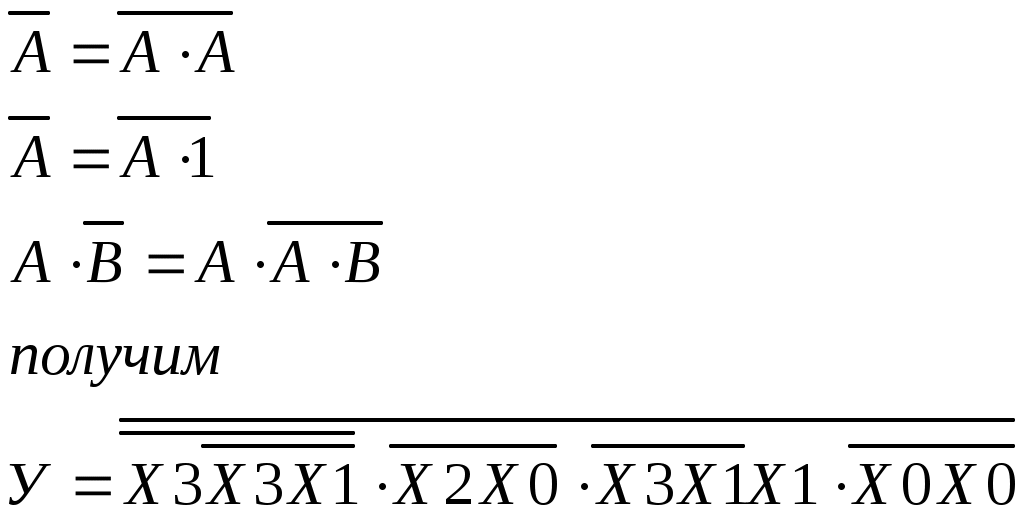
* Базис «ИЛИ-НЕ»
Таким же образом можно реализовать элементы базиса И, ИЛИ, НЕ через базис ИЛИ—НЕ
Реализация функции НЕ через функцию ИЛИ-НЕ:
Реализация функции И через элемент ИЛИ—НЕ: