Цель работы: изучение возможности аппроксимации с помощью нейронной сети прямого распространения.Аппроксимация представляет процесс приближения одних математических объектов другими, близкими к исходным. Эта замена позволяет свести задачу к изучению более простых или более удобных объектов и производить исследования их числовых характеристик и качественных свойств. Аппроксимация может сводиться к нахождению функциональной зависимости по имеющемуся набору данных. В нашем случае, функциональная зависимость будет представлена в нейросетевом базисе, т.е. через комбинацию активационных функций нейронных сетей. Согласно теореме, доказанной в 1989г. Л. Фунахаши, произвольно сложная функция может быть аппроксимирована двухслойной нейронной сетью, имеющей произвольные активационные функции. Поэтому часто для решения задачи аппроксимации используют нейронную сеть (НС), представляющую собой многослойный персептрон. В данной лабораторной работе для решения задачи аппроксимации предлагается использование трехслойной нейронной сети, содержащей входной, один скрытый и выходной слои. Первый (входной) слой содержит число нейронов, равное количеству входных факторов. Выходной слой содержит один нейрон, выдающий выходное значение чаще всего с линейной функцией активации. Второй (скрытый) слой содержит завышенное число нейронов равное, например, половине суммы числа обучающих данных, равное:Затем число нейронов скрытого слоя уменьшается до тех пор, пока ошибка аппроксимации не начнет возрастать. Чаще всего выбирается гиперболический тангенс. Предпочтительность использования сигмоидального тангенса в качестве функции активации связана с тем, что эта функция является гладкой, дифференцируемой, а

---

производная выражается через саму функцию, что позволяет снизить скорость обучения нейронной сети.

Для простейшего случая аппроксимации одномерной функции y  f (x) нейронная сеть выполняет функцию нахождения преобразования f (x) через функции активации. Число входов в случае одномерной функции равно 1 (х), число выходов – 1 (у).

Ход работы


Код программы:


public class cSensor
{
public event EventHandler ChangeState;
private sbyte state = 0;
public sbyte State
{
get { return state; }
set
{
state = value;
if (state == 1 && ChangeState != null)
{
ChangeState(this, new EventArgs());
}
}
}
}


public delegate void BackCommunication(sbyte Type);
class cSinaps
{
private sbyte type;
private BackCommunication hBackCommunication;
public cSinaps(sbyte tType,BackCommunication tBackCommunication)
{
type = tType;
hBackCommunication = tBackCommunication;
}
public void ChangeSensorState(object sourse, EventArgs e)
{
hBackCommunication(type);
}
}


public class cAssociation
{
public int ActivationLevel = 0;
private cSinaps[] oSinaps;
public cAssociation(cSensor[] sensorsField, int SCount, Random RND)
{
int SinapsCount = 10;
oSinaps = new cSinaps[SinapsCount];
int tSinapsNumber = 0;
int tmpSensorNumber = 0;
sbyte tmpSensorType = 0;
for (int j = 1; j < SinapsCount + 1; j++)
{
tmpSensorNumber = RND.Next(SCount);
if (RND.Next(2) == 0) tmpSensorType = 1; else tmpSensorType = -1;
oSinaps[tSinapsNumber] = new cSinaps(tmpSensorType, AssumeSinapsSignal);
sensorsField[tmpSensorNumber].ChangeState +=
new EventHandler(oSinaps[tSinapsNumber].ChangeSensorState);
tSinapsNumber++;
}
}
void AssumeSinapsSignal(sbyte Type)
{
ActivationLevel += Type;
}
}




public class cNeironNet
{
public cSensor[] SensorsField; /* Сенсорное поле*/
public cAssociation[] AssociationsFiled; /* Ассоциативное поле*/
int ACount;
int SCount;
public ArrayList AHConnections;
Random RND = new Random();
public cNeironNet(int argSCount, int argACount)
{
ACount = argACount;
SCount = argSCount;
SensorsField = new cSensor[SCount];
for (int i = 0; i < SCount; i++)
{
SensorsField[i] = new cSensor();
}
AssociationsFiled = new cAssociation[ACount];
for (int i = 0; i < ACount; i++)
{
AssociationsFiled[i] = new cAssociation(SensorsField, SCount, RND);
}
}
public ArrayList JoinStimul(int[] tPerception, int[] tReaction)
{
for (int i = 1; i < ACount + 1; i++)
{
AssociationsFiled[i].ActivationLevel = 0;
}
for (int i = 1; i < SCount + 1; i++)
{
SensorsField[i].State = 0;
}
//
for (int i = 0; i < SCount; i++)
{
SensorsField[i].State = tPerception[i];
}
AHConnections = new ArrayList();
for (i = 0; i < ACount; i++)
{
if (AssociationsFiled[i].ActivationLevel > 0)

---

{ AHConnections.Add(i); } } SaveReaction(tReaction); return AHConnections; } private void Storing() { for (int n = 1; n < 100000 + 1; n++) { for (int i = 1; i < StimulCount + 1; i++) { RAktivization(i); bool e = GetError(i); if (e) { LearnedStimul(i); Error++; } } } }}private void RAktivization(int ReactionNumber){ int[] Summa = new int[RCount + 1]; for (int j = 1; j < RCount + 1; j++) { for (i = 1; i < AHConnections[ReactionNumber].Count + 1; i++) { Summa[j] += Weight[AHConnections[ReactionNumber].Value[i]].Value[j]; } } for (int i = 1; i < RCount + 1; i++) { if (Summa[i] > 0) Reactions[i] = 1; if (Summa[i] <= 0) Reactions[i] = -1; }}private int GetError(int ReactionNumber){ int IsError = 0; for (int i = 1; i < RCount + 1; i++) { if (Reactions[i] == NecessaryReactions[ReactionNumber].Value[i]) { ReactionError[i] = 0; } else { IsError = 1; ReactionError[i] = NecessaryReactions[ReactionNumber].Value[i]; } } return IsError;}private void LearnedStimul(int ReactionNumber){ for (int j = 1; j < RCount + 1; j++) { for (int i = 1; i < AHConnections[ReactionNumber].Count + 1; i++) { Weight[AHConnections[ReactionNumber].Value[i]].Value[j] += ReactionError[j]; }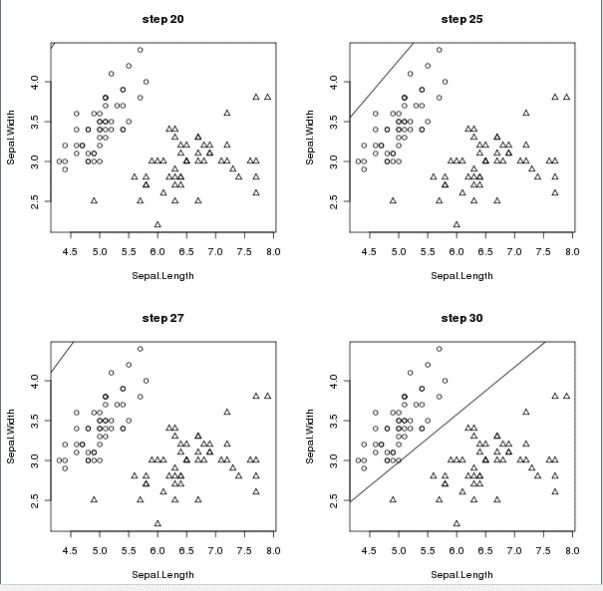Результаты выполнения программы:

---

Смотрите также файлы

• Контрольная работа по теме Компьютер. Обработка графической информации.docx

• Лекция методы формирования комплекса маркетинга.pdf

• Самостоятельная работа фио слушателя.docx

• Теоретическое обоснование Рынок пфи, валютный риск и инструменты хеджирования.rtf

• Восстановления исламской культуры в Республике Узбекистан.docx