Контрольная работа №1

Тема: «Линейные операторы и квадратичные формы»

Вариант №3

1. 
   Дан вектор x = 2e₁ + 2e₂ + 2e₃ + 2e₄. Разложить этот вектор по новому базису u₁, u₂, u₃, u₄, если u₁ = e₁ + e₂, u₂ = e₂ + e₃, u₃ = e₃ + e₄, u₄ = e₁ + e₄.
   
2. 
   Найти матрицу А^* оператора А =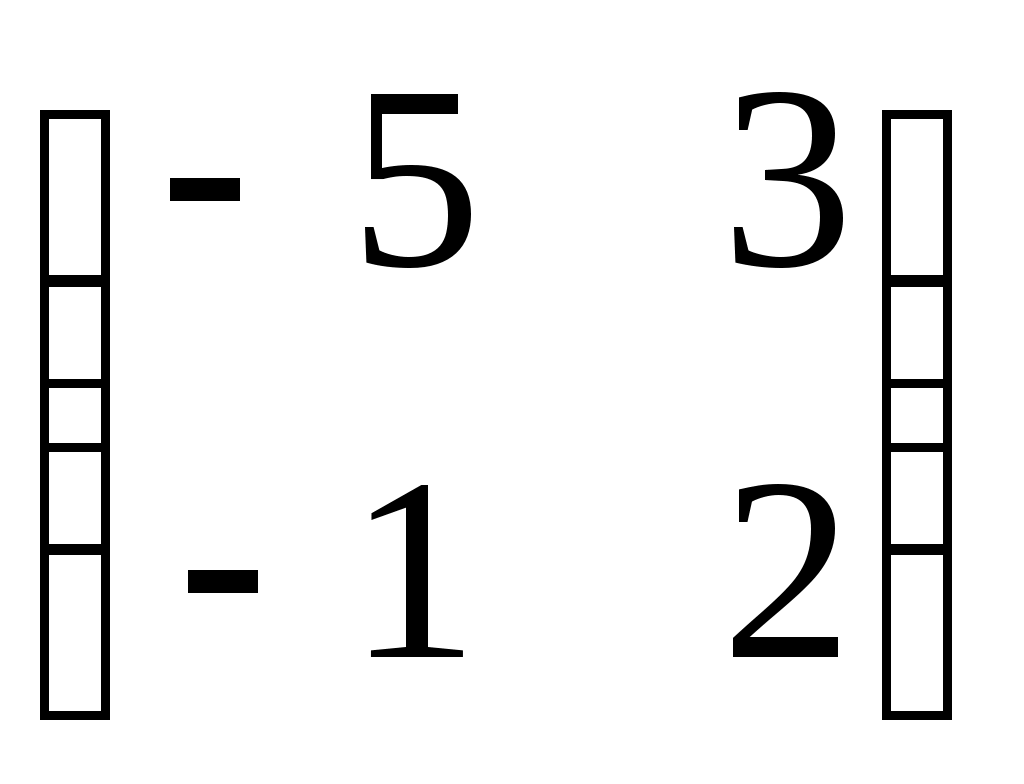 в базисе u₁ = -e₁ + 3e₂, u₂ = 2e₁ + e₂.
   
3. 
   Привести к каноническому виду квадратичную форму f(x,y) = 17x² + 12xy + 8y².
   

Контрольная работа №2

Тема: «Кривые второго порядка»

Вариант №6

1. 
   Привести к каноническому виду квадратичную форму x² + 25y² – 4x + 10y – 11 = 0. Классифицировать и изобразить кривую, определяемую этим уравнением.
   
2. 
   Составить каноническое уравнение: а) эллипса, если известно, что расстояние между фокусами равно 4, а расстояние между директрисами равно 5; б)гиперболы, если известно, что она проходит через точки P(–5,2) и Q(
   

Контрольная работа №3

Тема: «Комплексные числа»

Вариант №3

1. Решить уравнение:

.

2. Вычислить:

.

3. Вычислить значения корней и изобразить их на комплексной плоскости: .
Контрольная работа №4

на тему: «Многочлены»
Вариант № 6
1. Выполнить деление многочлена f(x) на многочлен g(x) с помощью метода неопределенных коэффициентов. Проверить результат делением «в столбик».

f(x) = 21x⁶ +6x⁵ +105x² + 30x; g(x) = 3x⁴ + 15.
2. Найти НОД многочленов.

3. Используя схему Горнера проверить, является ли значение x=1 корнем многочлена f(x).

Найти значение g(1).

---

Смотрите также файлы

• 44. 02. 02 Преподавание в начальных классах.doc

• Учебнометодическое пособие по выполнению дипломной работы для студентов по специальности 38. 02. 01 Экономика и бухгалтерский учет.doc

• Характеристика творчества Бенджамина Бриттена.docx

• Исполняющему обязанности начальника управления.docx

• Идз. Случайные величины.pdf