Файл: Конспект лекций Дисциплина Статистика.doc

Р
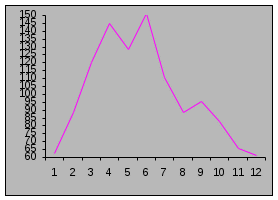
ис. 10. Индекс сезонности
Пример, определить индекс сезонности реализации свежих фруктов в магазинах города (тонн).

Месяц	Фактические данные			Выровненные			Фактические в % к выровненным			Js
	95	96	97	95	96	97	95	96	97
Январь	35	48	68	32,5	56,9	81	107,7	84,2	83,9	91,9
Февраль	30	42	55	34,9	58,9	83	85,9	71,3	66,3	74,5
Март	28	40	50	36,9	60,9	85	75,9	65,6	58,8	66,8
Апрель	25	36	42	38,91	62,9	87	64,3	57,2	48,3	56,6
Май	22	38	54	40,9	64,9	89,01	53,8	58,6	60,7	57,7
Июнь	38	46	65	42,9	66,9	91,02	88,6	68,8	71,4	76,3
Июль	52	70	90	44,9	68,97	93,02	115,8	101,6	96,8	104,7
Август	85	95	120	46,9	70,98	95,02	181,2	133,9	126,3	147,1
Сентябрь	92	115	145	48,9	72,98	97,03	188,1	157,8	149,4	165,1
Октябрь	80	102	130	50,9	74,98	99,03	157,2	131,2	131,2	141,6
Ноябрь	75	94	120	53,1	76,98	101,04	141,2	122,2	118,8	121,4
Декабрь	50	75	95	55,1	78,99	103,04	90,7	95,05	92,2	92,7

---

t	y	t2	yt	yt	t	y	t2	yt	yt
-17.5	35	306.25	-612.5	32.5	0.5	70	0.25	35	68.97
-16.5	30	272.25	-495	34.9	1.5	95	2.25	142.5	70.98
-15.5	28	240.25	-434	36.97	2.5	115	6.25	287.5	72.98
-14.5	25	210.25	-362.5	38.91	3.5	102	12.25	357	74.98
-13.5	22	182.25	-297	40.9	4.5	94	20.25	423	76.99
-12.5	38	156.25	-475	42.9	5.5	75	30.25	412.5	78.99
-11.5	52	132.25	-598	44.9	6.5	68	42.25	442	81
-10.5	85	11.25	-892.5	46.9	7.5	55	56.25	412.5	83
-9.5	92	90.25	-874	48.93	8.5	50	72.25	425	85
-8.5	80	72.25	-680	50.9	9.5	42	90.25	399	87
-7.5	75	56.25	-562.5	53.1	10.5	54	110.25	567	89.01
-6.5	50	42.25	-325	55.1	11.5	65	132.25	847.5	91.02
-5.5	48	30.25	-264	56.9	12.5	90	156.25	1125	93.02
-4.5	42	20.25	-189	58.9	13.5	120	182.25	1620	95.02
-3.5	40	12.25	-140	60.9	14.5	145	210.25	2102.5	97.03
-2.5	36	6.25	-90	62.9	15.5	130	240.25	2015	99.03
-1.5	38	2.25	-57	64.9	16.5	120	272.25	1980	101.04
-0.5	46	0.25	-23	66.9	17.5	95	306.25	1662.5	103.04

---

Для упрощения расчетов обозначим t, таким образом, чтобы сумма tбыла равна 0 и:

---

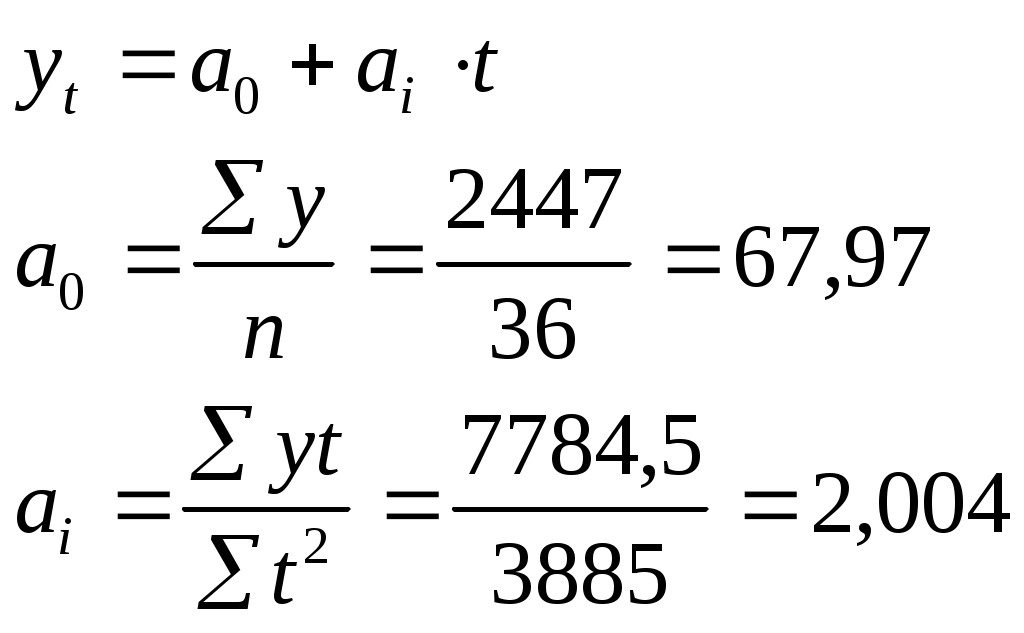
Тема 10. Индексы
1. Общие понятия об индексах.
Для характеристики явлений и процессов экономической жизни, статистика наряду с другими показателями использует индексы. Слово «индекс» в переводе – показатель.

Индекс – обобщающий показатель сравнения двух совокупностей, состоящих из элементов, которые непосредственно не подчиняются суммированию.

К совокупностям, элементы которых можно суммировать, относятся те совокупности, в которых дается сравнительная характеристика объемов: динамика посевных площадей, динамики выпуска конкретного вида продукции, динамики оплаты труда и т.д.

К совокупностям, элементы которых не поддаются суммированию, относятся такие 2 вида:

- характеристика 1 тонны пшеницы, молока, стали и т.д. В таких совокупностях рассчитывается индекс физического объема произведенной (проданной, потребленной) продукции;

- совокупности, где характеризуются цены (одной тонны пшеницы, молока и т.д.).

Для характеристики общего уровня цен (себестоимости, производительности, урожайности)применяются индексы себестоимости, цен и т.д.

Индексы применяются в следующих сферах:
1). Для сравнительной характеристики элементов конкретной совокупности;

2). Динамики;

3). Для пространственного сравнения;

4). Для сравнения факта с планом;

5). При факторном анализе.
2. Классификация индексов.
Индексы классифицируются по ряду признаков:
1. В зависимости от объектов исследования:

• 
  индексы объема (структуры);
  
• 
  качественные индексы (индексы цены, себестоимости).
  

2. По охвату:

• 
  индивидуальные индексы;
  
• 
  общие индексы;
  
• 
  групповые индексы.
  

Индивидуальные индексы – дают сравнительную характеристику отдельных элементов совокупности (индекс физического объема, себестоимости, производительности и т.д.).

Обозначается i.

Общие индексы – характеризуют изменение совокупности в целом, обозначают J.

Групповые индексы – охватывают не все элементы совокупности, а только отдельные части.

Групповые индексы рассчитывают с помощью метода группировок, собирая и группируя данные за период.
3. В зависимости от методологии расчета общие и групповые индексы делят на:

• 
  агрегатные;
  
• 
  средние из индивидуальных.
  

---

Агрегатные – основная форма экономических индексов.

Средние из индивидуальных – производная форма, они получаются путем расчета и преобразования агрегатных. Если совокупность состоит из 3 и более периодов, то может быть рассчитана цепная и базисная система индексов.
3. Принципы и методы исчисления общих индексов.

Для того, чтобы рассчитать общий индекс, необходимо преодолеть несуммарность отдельных элементов изучаемого явления, это достигается путем введения в индекс дополнительного неизменного показателя, тесно связанного с индексируемой величиной. Этот показатель называется весами агрегатного индекса или показателем сопряжения. Так, если индексируются цены, то для того, чтобы преодолеть несуммарность цен, цены умножают на количество.

Существует два правила построения общих индексов:
1. Если строятся индексы объема (структуры), то качественные величины берутся по базисным данным.
2. Если строятся индексы качества, то объемные величины берутся по отчетным данным.

Агрегатные индексы
В международной статистике для построения агрегатных индексов применяются следующие обозначения:
q – физический объем произведенной продукции (количество);

p – цена;

z – себестоимость;

d – структура (удельный вес);

1 – отчетный период;

0 – базисный период.
Пример.

Вид продукции	Ед. измерения, тыс.	Июль		Август		Индивидуальные индексы
		Кол-во	Цена, руб.	Кол-во	Цена, руб.	Физического объема	Цены
Молоко	Л	5000	300	6000	276	1,2	0,92
Мясо	Ц	25000	200	32000	190	1,28	0,95
Картофель	Т	10000	120	11000	102	1,1	0,85

---