7. Согласно ГОСТу 21153.8-88 определяем положение кругов Мора для 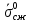и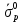













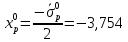
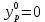
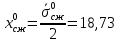
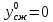
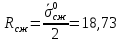
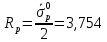
где 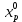, , 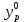, 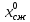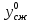– центральные точки кругов Мора для 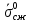и 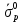соответственно, 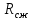и 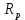- радиусы кругов Мора для 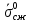и 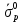соответственно.

8. Составим уравнения для построения кругов Мора для 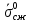и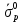





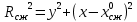
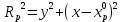
9. Построим паспорт прочности горной породы (рис. 1)



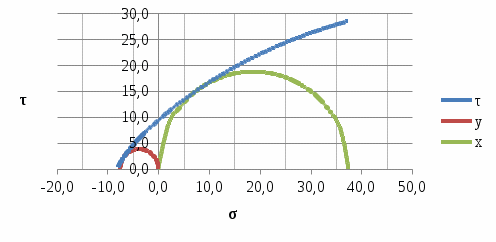
Рис. 1. Паспорт прочности горной породы

Задание 3. Определение нормальных и касательных напряжений, действующих по площадке.

Задача 1. Определить нормальное и касательное напряжения площадки, представленной на рис. 2.



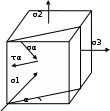
Рис. 2. Начальное условие к задаче 1

Таблица 4. Исходные данные к задаче 1

σ1, МПа	σ2, МПа	σ3, МПа	α, о
68	18	28	18

---

Решение

1. Перестроим рисунок для определения напряжений, действующих на площадку (рис. 3).



Рис.3. Представление напряжений на плоском изображении

2. Согласно рис. 3 и условию равновесия составим уравнения проекций, обозначив за а длину площадки,





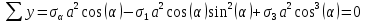
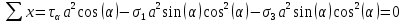
3. Отсюда получаем





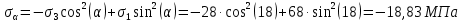
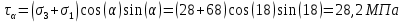
4. Получив ответ аналитическим методом, найдём решение задачи графически.

5. Строим круг Мора для 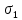и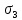

Таблица 5. Данные для построения круга Мора

σ	τ	σ	τ	σ	τ	σ	τ	σ	τ	σ	τ
-68	0	-50	37,47	-32	46,48	-14	47,62	6	40,35	24	19,18
-66	13,71	-48	38,99	-30	46,95	-12	47,33	8	38,99	26	13,71
-64	19,18	-46	40,35	-28	47,32	-10	46,95	10	37,47	28	0
-62	23,24	-44	41,57	-26	47,62	-8	46,48	12	35,78
-60	26,53	-42	42,66	-24	47,83	-6	45,91	14	33,88
-58	29,33	-40	43,63	-22	47,96	-4	45,25	16	31,75
-56	31,75	-38	44,5	-20	48	-2	44,5	18	29,33
-54	33,88	-36	45,25	-18	47,96	0	43,63	20	26,53
-52	35,78	-34	45,91	-16	47,83	2	42,66	22	23,24

---

6. Откладываем от центра окружности двойной угол α. На пересечении круга Мора и луча отложенного угла получаем точку с координатам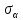и и 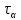(рис. 4).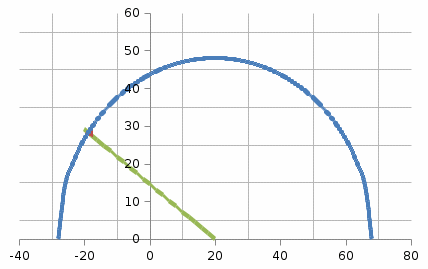



Рис. 4. Графическое решение задачи 1

Задача 2. Определить нормальное и касательное напряжения площадки, представленной на рис. 5.



Рис. 5. Начальное условие к задаче 2

Таблица 6. Исходные данные к задаче 2

σ1, МПа	σ2, МПа	σ3, МПа	α, о
48	28	18	13

Решение

1. Перестроим рисунок для определения напряжений, действующих на площадку (рис. 6).



Рис.6. Представление напряжений на плоском изображении

2. Согласно рис. 6 и условию равновесия составим уравнения проекций, обозначив за а длину площадки,





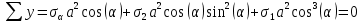
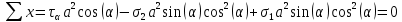
3. Отсюда получаем





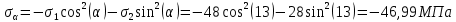
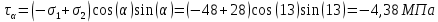
4. Получив ответ аналитическим методом, найдём решение задачи графически.

5. Строим круг Мора для и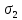

Таблица 7. Данные для построения круга Мора

σ	τ	τ
48	0,00	0,00
46	6,00	-6,00
44	8,00	-8,00
42	9,17	-9,17
40	9,80	-9,80
38	10,00	-10,00
36	9,80	-9,80
34	9,17	-9,17
32	8,00	-8,00
30	6,00	-6,00
28	0,00	0,00

---

6. Откладываем от центра окружности двойной угол α.(рис. 7). Отметим точку пересечения луча отложенного угла и круга Мора.



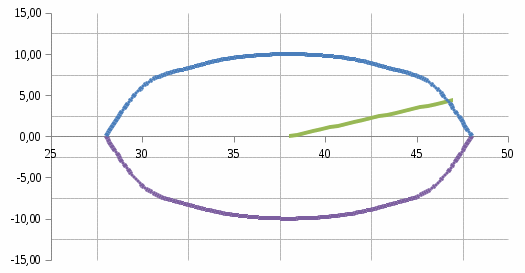
Рис. 7. Графическое решение задачи 2

7. Отметим, что точка с координатами и не принадлежит данному кругу, однако точка пересечения графиков имеет координаты 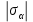и 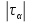. А это значит, что направления нормального и касательного напряжений направлены противоположно данным.

Задача 3. Определить нормальное и касательное напряжения площадки, представленной на рис. 8.



Рис. 8. Начальное условие к задаче 3

Таблица 8. Исходные данные к задаче 3

σ1, МПа	σ2, МПа	σ3, МПа	α, о
158	28	18	48

Решение

1. Перестроим рисунок для определения напряжений, действующих на площадку (рис. 9).



Рис. 9. Представление напряжений на плоском изображении

2. Согласно рис. 9 и условию равновесия составим уравнения проекций, обозначив за а длину площадки,





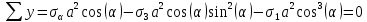
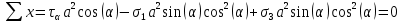
3. Отсюда получаем





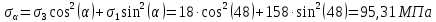
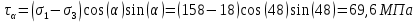
4. Получив ответ аналитическим методом, найдём решение задачи графически.

5. Строим круг Мора для и

Таблица 9. Данные для построения круга Мора

σ	τ	τ	σ	τ	τ	σ	τ	τ
18	0,00	0,00	67	66,78	-66,78	116	64,16	-64,16
25	30,51	-30,51	74	68,59	-68,59	123	60,62	-60,62
32	42,00	-42,00	81	69,65	-69,65	130	56,00	-56,00
39	49,99	-49,99	88	70,00	-70,00	137	49,99	-49,99
46	56,00	-56,00	95	69,65	-69,65	144	42,00	-42,00
53	60,62	-60,62	102	68,59	-68,59	151	30,51	-30,51
60	64,16	-64,16	109	66,78	-66,78	158	0,00	0,00

---

6. Откладываем от центра окружности двойной угол α.(рис. 10). Отметим точку пересечения луча отложенного угла и круга Мора.



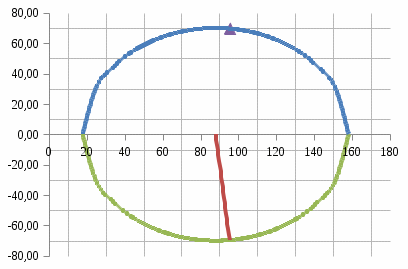
Рис. 10. Графическое решение задачи 3

7. Отметим, что значение σ в точке пересечения графиков и совпали, а значение τ и одинаковы по значению, но различны по знаку. Следовательно, направление должно быть противоположно данному.

Выводы по расчётно-графической работе

1. Мы провели статистическую обработку данных на одноосное сжатие и растяжение горной породы, чтобы в дальнейшем построить паспорт горной породы. Ознакомились с ГОСТом 21153.8-88 для определения 100% надёжности данных.

2. Выполнили построение паспорта объемной прочности горной породы аналитическим методом по данным одноосных испытаний. Благодаря кругам Мора смогли убедиться в верном построении паспорта, так как вписанные круги Мора одноосного растяжения и сжатия касаются огибающей только в одной точке.

3. Определили нормальные и касательные напряжения, действующие по площадке, аналитическим и графическим методом. Убедились в том, что методы верны, так как значения и совпадают в обоих методах с поправкой на знак (направление) напряжений.

---

Смотрите также файлы

• І нса і дегей.docx

• Учебные пособия и связанные с ними файлы. Пожалуйста, начните с этого руководства в формате pdf.docx

• Практическая работа 3 по теме Особенности конструирования современного урока географии.pdf

• " Грыжи передней брюшной стенки ".docx

• Оушыа бадарланан Балам дейтін жрт болмаса, жртым дейтін бала айдан болсын.docx