ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЗАТТАРДЫҢ КРИЗИСТІК КҮЙІ
Шахметова Айша Кайратовна, 6B01502 – Математика-Физика білім беру бағдарламасының 2-курс студенті, Қазақ ұлттық қыздар педагогикалық университеті, Алматы қ., Қазақстан
e-mail: ajsasahmetova@gmail.com
Ғылыми жетекшісі: физика магистрі, аға оқытушы Айдарбекова Акмарал Абылаевна
Түйіндеме.Нақты газдың теңдеуін түрлендіру арқылы изотермасын қарастыру. Кризистік нүктелер анықтамасымен танысып, Тк, Рк Vк формулаларын қорыту үшін иілу нүктесінің қасиетін қолдану. Клапейрон-Менделеев теңдеуін нақты газдар үшін қолдануға боламайтынын дәлелдеу.
Аннотация Рассмотрение изотермы реального газа путем преобразования уравнения. Ознакомиться с определением критических точек и применить свойство точки перегиба для обобщения формул Тк, Рк Vк. Доказательство того, что уравнение Клапейрона-Менделеева нельзя использовать для реального газа.
Кілт сөздері: нақты газдар, Ван-дер-Ваальс теңдеуі, изотермалық процесс, кризистік температура, кризистік қысым, кризистік көлем.
Нақты газдың тәжірибе жүзінде алынған изотермаларын идеал газ изотермасымен салыстырып көрейік. Нақты газдардың изотермаларын теориялық тұрғыда сызбасын салу үшін Ван-дер-Ваальс теңдеуін пайдаланамыз.
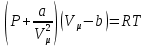(Ільясов Н., 2003)(1)
P – газға сырттан түсірілген қысым (газдың ыдыс қабырғаларына түсіретін қысымына тең)
а және b – әр газ үшін әртүрлі мәндерге ие болатын, тәжірибелер арқылы анықталатын Ван-дер-Ваальс тұрақтылары
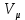– молярлық көлемR – тұрақты универсал газ тұрақтысы
Т – температура
Берілген 1 моль нақты газ үшін жазылған Ван-дер-Ваальс теңдеуіндегі жақшаларды ашамыз:
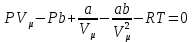
Шыққан теңдеуді
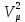-қа көбейтеміз:
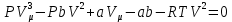немесе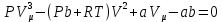 
Өрнектің екі жағында P – ға бөлген кезде, теңдеудің мына түрін аламыз:
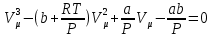
(2)
Сонымен,
көлемге қатысты үшінші дәрежелі алгебралық теңдеу алынды. Көлем үшінші дәрежелі болғандықтан, оның үш шешімі болады. Алайда осы үшінші дәрежелі теңдеудің үш түбірі де шын немесе екі түбірі жалған, бір түбірі шын болуы мүмкін. Бұл түбірлердің физикалық мағынасын түсіну үшін, Ван-дер-Ваальс теңдеуінің изотермасын (T=const), яғни тұрақты температурадағы көлем мен қысымның арасындағы тәуелділікті қарастырайық.
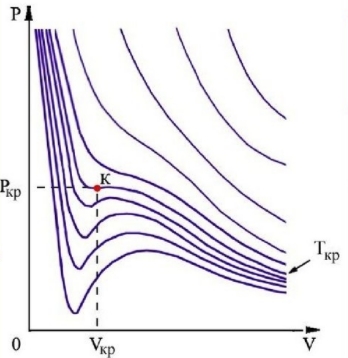P қысымның көлемге әртүрлі T=const температуралардағы тәуелділігін график түрінде кескіндесек, қатар келген изотермалар шығады. (Құлбекұлы М., 2017)Ван-дер-Ваальс теңдеуінің изотермасы бойынша, қандай да бір температурада қысымның бір мәнінде көлемнің үш мәні сәйкес келуі мүмкін.
Алайда, температураны төмендете берсек, мысалы, көмірқышқыл газы үшін
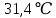температурада, изотермада иілу нүктесі пайда болады. Бұл нүктеден кейінгі изотермаларда максимумдар мен минимумдардың ажырауы басталады. Осы температура нүктесіне сәйкес көлем 
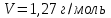, қысым P=73 атм. (Ільясов Н., 2003)Иілу нүктесінің анықтамасы бойынша: дифференцианалатын функцияның графигіндегі нүктесінің абцисасы бір кезде ойыс, бір кезде дөңес ойыстан дөңеске ауысатын нүктені иілу нүктесі деп аталады. (Темірғалиев Н., 1987.)
Көмірқышқыл газы үшін осы нүктеде, Ван-дер-Ваальс теңдеуіндегі көлемнің үш түбірінің айырмашылығы жойылады. Сонда белгілі бір Тk температурада көлемнің үш мәні бірігеді және заттардың үш фазасының айырмашылықтары болмайды. Бұл Тк кризистік температура деп аталады, ал оған сәйкес қысым мен көлем Рk кризистік қысым және Vk кризистік көлем деп аталады.( Ільясов Н., 2003)
Тk, Рk ,Vk мәндерін анықтау үшін Ван-дер-Ваальс теңдеуін математикалық түрде талдау арқылы алуға болады. Жоғарыдағы тұжырымдаманың негізінде Ван-дер-Ваальс изотермалары бойынша кризистік температурада нақты газ изотермасы иіледі. Бұл кризистік К нүктеде теңдеудің нақты үш шешімнің бірдей мәндерге ие болатынын көрсетеді. Осы нүктедегі кризистік көлемді табу үшін иілу нүктесінің қажетті теоремасын қолданамыз: “Егер f
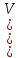
)функцияның (a,b) аралығында екінші ретті үзіліссіз туындысы бар болып
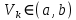нүкте осы функцияның иілу нүктесі болса, онда 
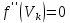” (Темірғалиев Н., 1987.)Сондықтан, осы иілу нүктесінде қысымның көлем бойынша алынған бірінші және екінші ретті туындысы нөлге теңеледі.
Ван-дер-Ваальс теңдеуінің максимумы мен минимумы Ферма теоремасы арқылы табылады: “Егер f
) функциясы үшін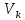 
локальді экстремум нүктесі болып, сол нүктеде f )-тің ақырлы туындысы бар болса, онда сол туындының мәні нольге тең болады” (Темірғалиев Н., 1987.)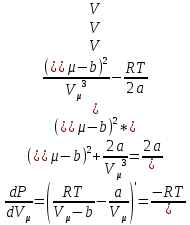
Сонда,
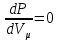шарты мына кезде орындалуы тиіс: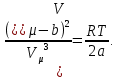 
(3)
Иілу нүктесінде қысымның көлем бойынша алынған екінші ретті туындысын тауып, нөлге теңестіреміз.
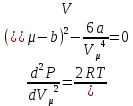
(4)
(4) теңдеуге (3) теңдеуден температураның мәнін тауып қойғанда, теңдік мына түрге келеді:
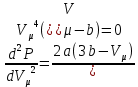
(5)
Теңдеуді шығару арқылы, кризистік көлемді табамыз:
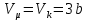
(6)
Егер
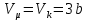мәнін (4) теңдеуге қойса, кризистік температура мәнін анықтауға болады: Тk =
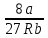
(7)
Алынған шамаларды (1) теңдеуіне қойып, кризистік қысымды табамыз.
Pk =
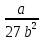
(8)
Қорытындылай келе,Тk, Рk ,Vk мәндерін пайдаланып:
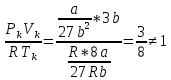,(9)
бұл қатынас газ табиғатына байланысты болмайды деген тұжырым шығады. Яғни, кризистік нүкте аймақта, әсіресе кризистік температурадан төмен температураларда Клапейрон-Менделеев теңдеуін қолдануға болмайтынынаа көз жеткізіледі.
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
-
Құлбекұлы М. Жалпы физика: оқу құралы. – Алматы: Қарасай, 2017. – 448 б. (76б.) -
Ілиясов Н. Жалпы физика курсы. Молекулалық физика және бейсызық физика: оқу құралы. – Алматы: Білім, 2003. – 352 б. (181б., 185-186б.,) -
Темірғалиев Н. Математикалық анализ. Бірінші бөлім. – Алматы: Мектеп, 1987. – 288б. (226б., 283б.)