Файл: Лабораторная работа 152 проверка теоремы штайнера работу выполнили студенты группы 03010 Коротков Алексей Плешаков Даниил Проверил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №152
ПРОВЕРКА ТЕОРЕМЫ ШТАЙНЕРА
Работу выполнили студенты группы: 03-010
Коротков Алексей
Плешаков Даниил
Проверил:
Теория:
Основное уравнение динамики вращательного движения в случае неподвижной оси вращения z удобно проектировать на эту ось:
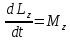
Здесь
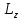 - проекция момента импульса,
- проекция момента импульса, 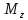 - момент внешних сил относительно оси.
- момент внешних сил относительно оси.Проекция момента импульса
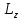 связана с угловой скоростью
связана с угловой скоростью  и моментом инерции I относительно этой оси:
и моментом инерции I относительно этой оси:
Момент инерции тела определяется формулой:

Где суммирование проводится по всем материальным точками тела с массами
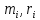 - расстояние от материальным точек до оси вращения. В случае непрерывного распределения масс эту формулу можно записать в интегральном виде:
- расстояние от материальным точек до оси вращения. В случае непрерывного распределения масс эту формулу можно записать в интегральном виде:
Момент инерции величина аддитивная
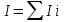
Момент инерции Iтела относительно любой оси AA´ можно найти, зная момент инерции
 относительно BB´, проходящей через центр масс тела паралельно оси AA´ при помощи теоремы Гюйгенса-Штайнера:
относительно BB´, проходящей через центр масс тела паралельно оси AA´ при помощи теоремы Гюйгенса-Штайнера: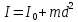
Где m – масса тела, d – расстояние между осями.
При вращении тела под действием момента упругой силы пружины уравнение приводит к следующему соотношению:
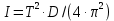
Где
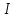 - момент инерции колеблющегося тела,
- момент инерции колеблющегося тела, 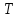 - период колебаний, D-модуль кручения пружины.
- период колебаний, D-модуль кручения пружины.
Цель работы
• Сравнение экспериментально определенной и теоретически показанной зависимости момента инерции диска от расстояния между осью симметрии диска и осью его вращения.
Решаемые задачи
-
Измерение моментов инерции диска для различных его положений методом крутильных колебаний.
Экспериментальная установка
Приборы и принадлежности:
-
Торсионная пружина на штативе. -
Секундомер. -
Исследуемый диск.
Ход работы.
-
Установили диск на торсионную пружину так, что бы ось колебаний проходила через отверстие 0. Измерили период колебаний .
. -
Последовательно устанавливали диск так, чтобы ось колебаний проходила через отверстия: 2,4,6,8,10,12,14,16. -
Измерили радиус диска. -
Вычислили относительные торические моменты инерции диска по формуле:
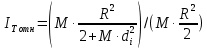 =
=
Для всех осей и сравнили с экспериментальными результатами, вычисленными с использованием данных измерения по формуле:
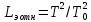
-
Данные измерений представили в виде таблицы:
| № | d,см | 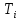 (1) (1) | 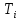 (2) (2) | 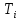 (3) (3) | 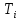 (4) (4) | 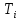 (5) (5) | 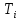 |  |
| 0 | | 2,453 | 2,488 | 2,434 | 2,419 | 2,475 | | |
| 2 | | 2,485 | 2,543 | 2,532 | 2,493 | 2,535 | | |
| 4 | | 2,555 | 2,545 | 2,555 | 2,553 | 2,557 | | |
| 6 | | 2,752 | 2,762 | 2,756 | 2,756 | 2,760 | | |
| 8 | | 2,836 | 2,835 | 2,782 | 2,773 | 2,800 | | |
| 10 | | 3,082 | 3,078 | 3,084 | 3,076 | 3,070 | | |
| 12 | | 3,183 | 3,176 | 3,215 | 3,217 | 3,196 | | |
| 14 | | 3,642 | 3,656 | 3,662 | 3,648 | 3,652 | | |
| 16 | | 3,738 | 3,735 | 3,763 | 3,758 | 3,740 | | |
-
Построили график зависимости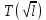 . Выделили на нём линейный участок. По точкам этого участка, пользуясь выражением
. Выделили на нём линейный участок. По точкам этого участка, пользуясь выражением 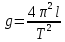 нашли ускорение свободного падения.
нашли ускорение свободного падения.

-
С помощью программы Excel рассчитали значение g для каждого опыта.
| N | l,см |  ,c ,c |  |
| 1 | 6,5 | 5,2 | 9,480385 |
| 2 | 6,5 | 5,05 | 10,05194 |
| 3 | 6,5 | 5,12 | 9,778961 |
| 4 | 10 | 6,38 | 9,688977 |
| 5 | 10 | 6,2 | 10,25973 |
| 6 | 10 | 6,45 | 9,479815 |
| 7 | 20 | 8,8 | 10,18554 |
| 8 | 20 | 8,89 | 9,98035 |
| 9 | 20 | 9 | 9,737877 |
| 10 | 30 | 10,91 | 9,940107 |
| 12 | 30 | 11 | 9,778116 |
| 13 | 30 | 11,14 | 9,533891 |
| 14 | 40 | 12,8 | 9,628516 |
| 15 | 40 | 12,54 | 10,03192 |
| 16 | 40 | 12,6 | 9,936609 |
| 17 | 50 | 14,2 | 9,779409 |
| 18 | 50 | 14,84 | 8,954091 |
| 19 | 50 | 14,7 | 9,125457 |
| 20 | 60 | 15,42 | 9,951803 |
| 21 | 60 | 15,11 | 10,36434 |
| 22 | 60 | 15,68 | 9,624505 |
| 23 | 70 | 16,43 | 10,22686 |
| 24 | 70 | 16,6 | 10,01846 |
| 25 | 70 | 16,5 | 10,14027 |
| 26 | 80 | 18,12 | 9,609325 |
| 27 | 80 | 18,01 | 9,727066 |
| 28 | 80 | 17,87 | 9,880073 |
| 29 | 90 | 19,12 | 9,709258 |
| 30 | 90 | 19,2 | 9,628516 |
| 31 | 90 | 18,95 | 9,884242 |
| 32 | 100 | 20,11 | 9,752033 |
| 33 | 100 | 20,1 | 9,761739 |
Среднее значение g=9,800943
Вывод: таким образом с помощью математического мы смогли определить примерное значение ускорения свободного падения.
Мы научились определять скорость свободного падения с помощью математического маятника.