ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Научно практическая конференция
«Первые шаги в науку»
Исследовательская работа на тему:
Моделирование электрических полей.
Выполнил:
Красков Роман,
ГУ «Верх-Березовская СШ»,
10 класс
Научный руководитель:
Коряко Евгений Ильич,
ГУ «Верх-Березовская СШ»,
Учитель физики и информатики
Содержание
-
Введение…………………………………………………………. -
Электрическое поле……………………………………………... -
Напряженность поля…………………………………………….. -
Силовые линии…………………………………………………... -
Моделирование силовых линей на компьютере………………. -
Заключение………………………………………………………. -
Список литературы ……………………………………………... -
Приложение 1……………………………………………………. -
Приложение 2……………………………………………………. -
Приложение 3…………………………………………………….
Введение
Для наблюдения того или иного явления в физике очень часто используется такой метод, как моделирование. Моделирование представляет собой воспроизведение определенных свойств и связей объекта - оригинала в другом, специально созданном объекте – в модели с целью их более тщательного изучения.
Форму силовых линий можно наблюдать при помощи кусочков бумажек, манной крупы или бумажных султанчиков, но данная модель не дает четкого представления о напряженности поля в каждой точке. Часто на опытах мы наблюдаем не определенную картину, например пересекающиеся линии в опыте с манной крупой. Однако, ЭВМ позволяет создать широкий спектр программных средств и активно использовать их процессе наблюдения, что позволяет более точно исследовать электрическое поле. Уже существующие программы для наблюдения силовых линии имею некоторые недостатки, например пользователь не может задавать величину зарядов, расстояние между зарядами, плотность линий, т.е. в них отсутствует возможность исследования поля. Решение этой проблемы я постараюсь воплотить в своем проекте.
Выполняя данную работу, я поставил цель, написать программу, которая позволит наблюдать и исследовать при помощи компьютера электрическое поле двух точечных.
Задачи исследования:
-
Изучить методы графического представления силовых линий. -
Изучить способ моделирования на компьютере при помощи постепенного наращивания h. -
Написать программу при помощи, которой можно провести эксперимент по исследованию электрических полей при помощи компьютера.
Электрическое поле
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами.
Возникновение сил, раздвигающих листочки электроскопа с поднесенным к нему заряженным телом, указывает на то, что вокруг заряда существует электрическое поле, через посредство которого и происходит действие указанных сил.
До Фарадея ученые считали, что электрические заряды действуют друг на друга непосредственно на расстоянии (теория дальнодействия). Среде, окружающей заряды, никакой роли не отводилось. Фарадей уже объяснял взаимодействие наэлектризованных тел как физический процесс, распространяющийся в промежуточной среде. Приписывая основную роль среде, окружающей заряды, Фарадей создал учение об электрических полях.
Электрическое поле – особый вид материи, создаваемый электрическими зарядами, основное свойство которого заключается в действии на другие электрические заряды.
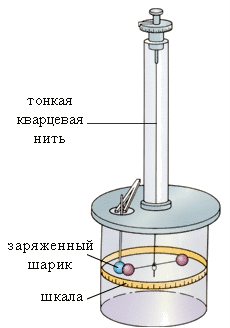
Впервые закон взаимодействия неподвижных зарядов был установлен французским физиком Ш. Кулоном (1785 год). В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (Приложение 1), отличавшихся чрезвычайно высокой чувствительностью.
Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
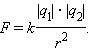
Силы взаимодействия подчиняются третьему закону Ньютона:
Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках.
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Коэффициент пропорциональности
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
Коэффициент k в системе СИ обычно записывают в виде:
где
Характеризует электрическое поле действие электрических сил, которому подвергается всякое помещенное в нее другое заряженное тело. На незаряженное тело электрические силы не действуют. Поэтому человек не ощущает электрическое поле ни одним из органов чувств.
Положим, что электрическое поле создано «точечным» положительным зарядом Q, т.е. Q – источник поля.
Внесем в поле пробный положительный заряд q, поместив его в точке В на расстоянии r от источника поля. На заряд q действует сила F. Величина этой силы зависит от внесенного в поле заряда q и от самого поля (заряда Q). По закону Кулона сила F пропорциональна и Q, и q. Но возьмем отношение
оно уже не зависит от величины пробного заряда и может служить характеристикой поля в точке В. Таким образом, мы приходим к величине, называемой напряженностью электрического поля.
Напряженность поля
Напряженность электрического поля в данной точке поля есть величина, численно равная силе, с которой поле действует на единицу положительного заряда, помещенного в данную точку поля.
Напряженность есть векторная величина. Таким образом, для характеристики поля надо указать и направление поля, за которое принимается направление силы, действующей на положительный заряд. Если электрическое поле образовано двумя точечными зарядами, напряженность поля в каждой точке мы найдем, применяя правило сложения векторов.
Силовые линии
Для наглядного изображения электрического поля Майклом Фарадеем были введены линии напряженности.
Силовые линии – это такие линии, в каждой точке которых вектор напряженности направлен по касательной к этой линии.
Силовые линии электростатического поля не замкнуты: они начинаются в положительных электрических зарядах (или в бесконечности) и заканчиваются в отрицательных электрических зарядах (или в бесконечности).
Линии напряженности не пересекаются и не имеют общих точек (за исключением точек, где напряженность равна нулю).
Количество линий напряженности, выходящих или входящих в данный заряд прямопропорционально абсолютной величине данного заряда. В пространстве можно провести любое число линий напряженности, причем через данную точку пространства проходит единственная линия напряженности (это следует из того, что линии напряженности не пересекаются).
По графическому изображению линий напряженности можно судить и о величине электрического поля: чем гуще расположены линии напряженности, тем больше напряженность в данной точке поля.
Моделирование силовых линий на компьютере
Итак, нам известно, что в каждой точке линии напряженности вектор напряженности направлен по касательной к этой линии. То есть, фактически, нам надо знать направление вектора напряженности в данной точке пространства.
Направление вектора можно просчитать с помощью метода координат: соответствующие координаты вектора суммы равны сумме соответствующих координат векторов-«слагаемых». Таким образом, для направления вектора мы получаем двойку чисел (x; y), которые являются координатами радиус-вектора суммы.
Просчитав направление результирующего вектора напряженности, из данной точки строим линию, с таким же направлением, как и вектор напряженности. На данной линии от данной точки по направлению вектора напряженности откладываем расстояние h. Для большей точности надо сделать так, чтобы h→0, однако тогда построение займет достаточно много времени, поэтому необходимо найти такое h, чтобы отношение «качество-время» было бы оптимальным.
Отложив величину h, мы получаем следующую точку, с которой проделываем те же самые операции. Код программы представлен в приложении 3.
Необходимо также учитывать, что для положительных зарядов направление откладывания величины h и вектора напряженности совпадают, а для отрицательных зарядов эти направления противоположно направлены.
Усилия, которые придется затратить при вводе этой программы и её отладки, окупятся, так как, меняя исходные данные, можно будет получать поля для различных соотношений между зарядами. В приложении 2 дано изображение полей для Q2=4*Q1.
Заключение
Результатом моей работы стала программа, которая может применяться как демонстрация теоретического материала, изложенного на уроке физики. Кроме того, программа позволяет заниматься поверхностной исследовательской деятельностью.
Список возможностей программы:
-
По данному электрическому полю рисовать общий план линий напряженности, с возможностью изменения параметров. -
По данному электрическому полю исследовать линии напряженности (т.е. строить через заданную точку линию напряженности). -
По данному электрическому полю вычислять напряженность и потенциал в заданной точке поля.
Данный проект разработан в рамках школьной научной секции учащихся ГУ «Верх – Березовская СШ»
СПИСОК ЛИТЕРАТУРЫ
1) Б.А. Кронгарт Учебник по физике 10 класс для школ естественно-математического направления.
2) Бурсиан Э. В. Задачи по физике для компьютера. – М.: Просвещение, 1991.
3) Открытая физика. Полный интерактивный курс физики на компакт-диске Ч. 2 / Под ред. Козела С. М. - М.: ООО Физикон, 2002.
.
Приложение 1