Таблица 5. Корреляционная матрица для трех переменных

Матрица корреляцийa
		x1	x3	x2
Корреляция	x1	1,000	,038	,246
	x3	,038	1,000	-,234
	x2	,246	-,234	1,000
a. Детерминант = ,879

Таблица 6. Корреляционная матрица для четырех переменных

Матрица корреляцийa
		x1	x3	x2	x4
Корреляция	x1	1,000	,038	,246	,703
	x3	,038	1,000	-,234	-,122
	x2	,246	-,234	1,000	,168
	x4	,703	-,122	,168	1,000
a. Детерминант = ,424

Как видно из этих таблиц, в первом варианте (определитель равен 0,999) мультиколлинеарность невыражена, и практически равна 1, что говорит о надежности результатов множественной регрессии. Во втором варианте (0,879) с добавле­

---

нием новой независимой переменной x2происходит некоторое появление, но определитель все равно остается достаточно большим. Но для третьего варианта, последобавления переменной x4, можно гово­рить о появлении достаточно выраженной мультиколлинеарности – определитель уменьшается в 2 раза (0,424). Отсюда следует, что данная переменная практически линейно не связа­на с другими.

4. Дать оценку полученного уравнения на основе коэффициента детерминации и общего F-критерия Фишера.

Максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости. , где уровень значимости берется равным 0,05. Вычисляется критическое значения с помощью функции ExcelFРАСПОБР, которая возвращает обратное значение для одностороннего F-распределения вероятностей. Степени свободы берутся соответственно 1 и 14.

При сравнении фактического и критического значений F-критерия Фишера для оценивания статистической надежности результатов регрессионного моделирования, выясняется, что лучшей моделью является первая модель ( , но вторая модель () также является надежной. Это означает, что гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

Квадрат коэффициента корреляции Rесть индекс детерминации, определя­ющий качество построенной модели. Чем ближе R²к единице, тем лучше регрессия описывает связь между независимыми и зависимой пере­менной. В нашем случае, как видно из таблицы 3, коэффициенты детерминации в обеих моделях не высокий, но достаточно значимый, во второй модели достигает практически 0,6. Значения R²и скорректирован­ного R²существенно различаются, это говорит о том, что используется слишком много независимых переменных при недостаточном объеме выборки. В таком случае скорректированныйR²за­служивает большего доверия.

По своему математическому смыслу R²

---

характеризует долю от общей диспер­сии зависимой переменной Y, объясняемую регрессией. Иначе говоря, коэффи­циент детерминации определяется как отношение дисперсии, обусловленной регрессией, к общей регрессии.

5. Выполнить анализ результатов, построить прогноз уровня результата, указав, при каких условиях он будет возрастать и при каких – снижаться.

Используя аналитическую систему SPSS, я получил следующие данные по коэффициентам:


Таблица 7. Коэффициенты

Модель		Нестандартизованные коэффициенты		Стандартизованные коэффициенты	t	Знч.	95,0%% доверительный интервал для B
		B	Стд. Ошибка	Бета			Нижняя граница	Верхняя граница
1	(Константа)	11,149	12,922		,863	,403	-16,567	38,864
	x1	1,401	,395	,687	3,542	,003	,553	2,249
2	(Константа)	-,381	12,323		-,031	,976	-27,004	26,242
	x1	1,371	,345	,673	3,968	,002	,624	2,117
	x3	7,703	3,320	,393	2,320	,037	,531	14,876

---

t_табл для числа степеней свободы df=n-2=16-2=14 и =0,05 по таблице составит 2,144.

Для первой модели:

Случайные ошибки :



.

Фактическое значение не превосходит табличное, поэтому гипотеза не откланяется, правда превосходит, т.е. статистически значим.

Доверительные интервалы:

;

;

;

;

Анализ границ доверительных интегралов приводит к выводу о том, чтотолько параметрb₁является статистически значимым.

Если прогнозные значения факторов составят 102,9% от их среднего уровня, то , то

Ошибка прогноза:



Предельная ошибка прогноза:

.

Доверительный интервал прогноза:

;

;

;

Диапазон границ доверительного интервала:

.

Для второй модели:

Случайные ошибки :

---

.

Доверительные интервалы:

;

;

;

;

;

;

Анализ границ доверительных интегралов приводит к выводу о том, чтотолько параметры b₁и b₂ являются статистически значимыми.

Если прогнозные значения факторов составят 102,9% от их среднего уровня, то , , то

Ошибка прогноза:



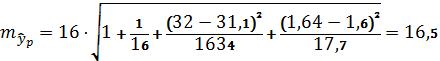
Предельная ошибка прогноза:

.

Доверительный интервал прогноза:

;

;

;

Диапазон границ доверительного интервала:

.
Выводы:

• 
  я рассмотрел множественную линейную регрессию и ее характеристики;
  
• 
  я закрепил навыки решением типовой задачи на основе использованияIBMSPSSStatistics.
  

Данная работа скачена с сайта Банк рефератов http://www.vzfeiinfo.ru. ID работы: 26976

Данная работа скачена с сайта Банк рефератов http://www.vzfeiinfo.ru. ID работы: 26976

---

Смотрите также файлы

• Агностицизм приобрел свою классическую форму в произведениях.docx

• М. Кирова Институт леса и природопользования.docx

• Справочник по психологии и психиатрии детского и подросткового возраста. Спб., 2000.docx

• Определите тип структуры по описанию ниже.doc

• Понятие, объект и субъект биржевых сделок.rtf