Контрольная работа
По дисциплине: Оптоэлектроника и интегральная оптика

ОЭиИО


Фамилия:

Имя:

Отчество:

№ зачетной книжки

Группа №:

Проверил: _____________


Санкт-Петербург

2023

Задача 1

Условие: Найти, чему равна собственная концентрация свободных носителей заряда в кремнии Si, германии Ge и арсениде галлия GaAs при

комнатной температуре T = 300K и температуре жидкого азота T = 77 K.

Решение: Концентрация собственных носителей заряда n_i имеет сильную температурную зависимость и определяется как:



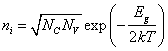
где эффективная плотность состояний в C и V зонах Nc,v также зависит от температуры T и эффективной массы носителей заряда в зоне m^*:



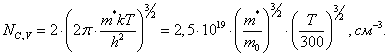
Ширина запрещенной зоны Eg имеет слабую зависимость от температуры типа Eg =Egо – αТ. Величины Egо и α приведены в таблице "Свойства полупроводников при Т=300 К", там же можно найти величины Nc и Nv . Расчет значений эффективной плотности состояний в C и V зонах и концентрации собственных носителей заряда n_i при температуре жидкого азота 77 K приводится ниже.

	Si	Ge	GaAs
Nc, см-3	3.6 × 1018	1.4 × 1019	5.8 × 1016
Nv,cм-3	1.4 × 1018	6.9 × 1018	9.8 × 1017
ni,см-3	3 × 10-20	1.4 × 10-7	2.8 × 10-33

Задача 2

Условие: Кремний Si и арсенид галлия GaAs легированы донорной примесью до концентрации N_D = 10¹⁷ см^-3. Считая примесь полностью ионизованной, найти концентрацию основных и неосновных носителей заряда при температуре Т = 300 K.

Решение:

Примесь полностью ионизована, когда концентрация равновесных электронов равна концентрации легирующей примеси n

---

₀=N_D. Из основного соотношения для полупроводников: n₀ × p₀=n_i². Найдем концентрацию неосновных носителей заряда: p₀=n_i²/n₀.

Для Si: .

Для GaAs: .

Задача 3

Условие: Рассчитать объемное положение уровня Ферми φ₀ относительно

середины запрещенной зоны в собственных полупроводниках – кремнии

Si и антимониде индия InSb при температурах T₁ = 300 K и T₂ = 77 K (с

учетом различных значений эффективных масс электронов и дырок).

Решение:

В собственном полупроводнике n₀ = p₀, и положение уровня Ферми относительно середины запрещенной зоны полупроводника φ₀ можно рассчитать как:

φ0, (эВ)	300 K	77 K
Si	-0.0124 эВ	-0,0032 эВ
InSb	+0,074 эВ	+0,019 эВ

Таким образом, в кремнии уровень Ферми лежит ниже, а в антимониде индия выше середины запрещенной зоны полупроводника E_i.



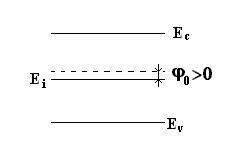
Зонная диаграмма полупроводника, когда: φ₀>0, m^*_p>m^*_e.

Задача 4

Условие: Полупроводники кремний Si, германий Ge и арсенид галлия GaAs

легированы донорной примесью до концентрации

---

N_D = 10¹⁵ см^-3.

Найти граничную температуру Т_гр, при которой собственная концентрация носителей заряда n_i еще ниже концентрации основных носителей заряда n₀.

Решение:

Известно, что E_g и N_c,v зависят от температуры. Для оценки граничной температуры пренебрежем этим фактом. Тогда, учитывая, что n₀=N_D и n₀=n_i, после преобразования получим:

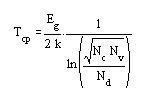
	Si	Ge	GaAs
Tгр ,К	668	439	1104
Тгр ,оС	395	166	831

Задача 5

Условие: Образец арсенида галлия GaAs подвергается внешнему воздействию, в результате которого генерируется 10²⁰ см^-3 ·c^-1 электронно-дырочных пар. Уровень легирования N_D = 2·10¹⁵ см^-3,

время жизни τ₀ = 5·10^-8 с, Т = 300 К.

Вычислить:

1. коэффициент рекомбинации;

2. избыточную концентрацию неосновных носителей заряда.

Решение:

Коэффициент рекомбинации r получим из соотношения:

G = R = r · n · p.

G = r · ( n + p ) = r·( n₀ + Δn+ p₀ + Δp ) = r · Δn· ( n₀ + p₀ ) = r · Δn · n₀.

Отсюда имеем для:

r = ( G / Δn ) · ( 1 / τ₀n₀ ) =10^–8 см³c^–1,

избыточная концентрация электронов Δn = G · τ0 = 5 · 10¹² см^–3.

---

Смотрите также файлы

• Паронимы в русском языке Понятие паронимы.pptx

• Бір дірет бізді мірге жолдайды. Біз мірді тсінбейміз.docx

• Иркутский государственный университет Институт математики, экономики и информатики.docx

• Занятия 3.doc

• Пвавапвава пвавапвава.rtf