Файл: ОЗО-лекции комп мм.doc

Компьютерная научная графика. Понять по графику свойства сложной функции человеку гораздо легче, чем из соответствующей формулы, хотя в ней информации, строго, говоря, гораздо больше. Так уж устроено человеческое восприятие, что рисунки, пусть даже условные, гораздо легче воспринимаются рассудком, чем сложные формулы или колонки чисел.

В современной прикладной информатике этим обстоятельством очень широко пользуются, и в ней сформировалось соответствующее направление - машинная (компьютерная) графика. По определению, машинная графика - раздел информатики, в рамках которого исследуются и разрабатываются технические, математические, программные и методические средства и приемы использования ЭВМ для создания, обработки, хранения и практического применения графических изображений. В машинной графике выделяют несколько разделов.

Иллюстративная графика, простейшими программными средствами которой являются всем знакомые диалоговые программы - графические редакторы. Она служит для создания изображений. Это - средство реализации воображения.

Деловая графика существенно «скучнее». Когда бухгалтеру, экономисту и т.д. нужно перевести сухие колонки чисел в столбчатую диаграмму, круговую диаграмму, график, достаточно вызвать такую программу и в ходе диалога сообщить ей заголовки, подписи, разметки, цвета и т.д. и имя файла, в котором по определенным правилам записаны указанные числа. Система построит заданное изображение на экране, выведет его на принтер.

Одна из самых сложных и специализированных разновидностей систем машинной графики - инженерная графика, известная также под именем САПР - системы автоматизированного проектирования. Это диалоговые системы, предназначенные для автоматизации процесса проектирования технических объектов, создания полных комплектов проектных документов с учетом существующих норм стандартов.

И, наконец, научная графика - наиболее актуальная для изучаемого курса и наименее всех допускающая единое описание. Универсальных систем компьютерной научной графики, по-видимому, не существует из-за огромного разнообразия задач. Часто программы, реализующие наглядное изображение решения научной задачи (почти всегда по итогам математического моделирования), встраиваются внутрь основной программы, пишутся на том же самом языке программирования.

Общую цель научной графики можно сформулировать так: сделать невидимое и абстрактное «видимым». Берем последнее слово в кавычки, так как часто эта «видимость» весьма условна. Можно ли увидеть распределение температуры внутри неоднородно нагретого тела сложной формы без введения в него сотен микродатчиков, т.е., по существу, его разрушения?- Да, если есть соответствующая математическая модель, и, что очень важно - договоренность о восприятии определенных условностей на рисунке.

Более того, можно «увидеть» и то, что строго говоря, вообще плохо соответствует слову «видеть». Так, квантовая химия дает нам возможность «увидеть» строение молекулы. Эти изображения верх абстракции и системы условностей, так как в атомном мире обычные наши понятия о частицах (ядрах, электронах и т.д. ) принципиально не применимы. Однако, многоцветное «изображение» молекулы на экране компьютера для тех, кто понимает всю меру его условности, приносит большую пользу, чем тысячи чисел, являющихся результатами расчета.

При решении относительно несложных задач нашего курса при построении траекторий движения тел, графиков целесообразно ориентироваться на тот язык программирования, на котором реализуется математическая модель.

Условные цвета, условное контрастирование. - Условная раскраска – это один из интересных приемов современной научной графики. Она находит широчайшее применение в самых разных приложениях науки и представляет собой максимально удобную, хотя и очень условную, визуализацию результатов компьютерного моделирования.

Приведем примеры. В различных исследованиях температурных полей встает проблема наглядного представления результатов. Самый простой (и, с точки зрения специалиста, весьма неэффективный) - привести карту (чертеж, план), в некоторых точках которой обозначены значения температуры.

Другой способ - набор изотерм - гораздо эффективнее; к нему прибегают некоторые газеты, давая состояние и прогноз погоды. Но можно добиться еще большей наглядности, учитывая, что большинству людей свойственно, сравнивая разные цвета, воспринимать красный как «горячий», голубой как «холодный», а все остальные - между ними.

Допустим, что на некоторой территории температура в данный момент имеет в разных местах значения от -25°С до + 15°С. Разделим этот диапазон на участки с шагом, равным, например, 5°

[-25,-20],[-20,-15],..„[+10,+15].

Затем закрасим первый из участков в ярко-голубой, последний - в ярко-красный, а все остальные - в промежуточные оттенки голубого и красного цветов. Получится замечательная, наглядная картина температурного поля.

СВОБОДНОЕ ПАДЕНИЕ ТЕЛА С УЧЕТОМ СОПРОТИВЛЕНИЯ СРЕДЫ

Второй закон Ньютона.

В рассматриваемых ниже физических задачах фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько, то равнодействующей, т.е. векторной сумме сил) и обратно пропорционально его массе:

В ситуации, когда сила или масса не являются величинами постоянными, необходимо записать этот закон в более общей математической форме.

Допустим, что сила или масса (или и то, и другое) непостоянны и заданным образом зависят от времени, скорости движения или перемещения: и . Достаточно хотя бы одной зависимости, чтобы ускорение было величиной переменной. Тогда формула Ньютона определяет значение ускорения в тот момент времени, которому соответствуют сила и масса. Интерес представляет временная зависимость перемещения и скорости.

Поскольку ускорение есть приращение скорости, а скорость — приращение перемещения, то

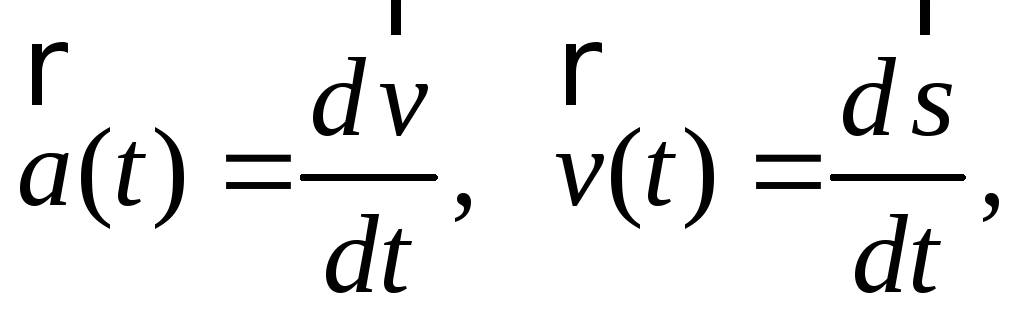
(1)

а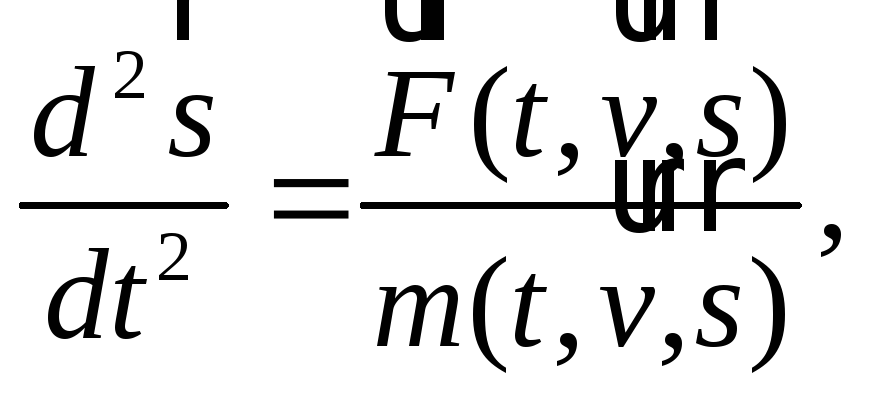сам второй закон Ньютона приобретает вид

(2)

и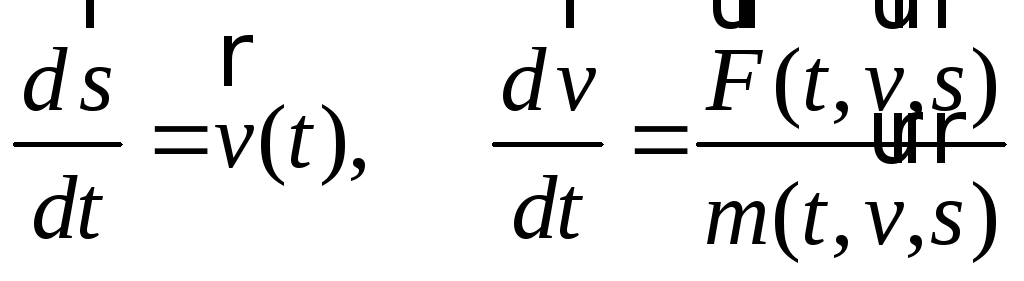ли, что то же самое,

(3)

Произведем дискретизацию по времени. Пусть в начальный момент времени t₀ величина s имеет значение s_0, а величина v – значение v₀. Тогда в некоторый последующий момент времени будем иметь

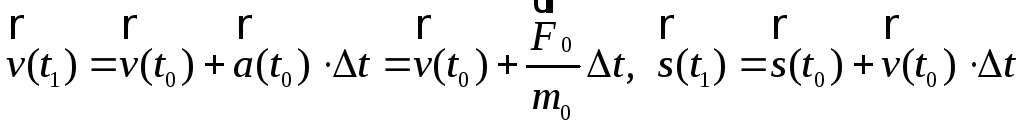
(4)

В последующие моменты времени можно поступать аналогично (4). Так, если известны значения v_i, и s_i в момент t_i , то

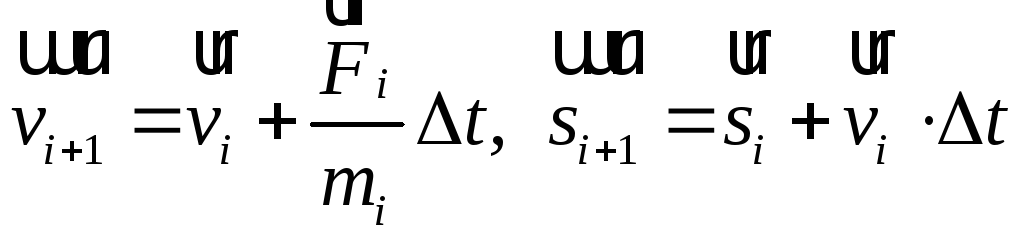
(5)

Сила сопротивления.

При реальных физических движениях сила сопротивления накладывает огромный отпечаток на характер движения.

О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости V (хотя это утверждение не является абсолютным).

При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение

где определяется свойствами среды иформой тела.

Например, для шарика – это формула Стокса, где -динамическая вязкость среды, r— радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм: = 0,0182 Н·с/м²,

для воды = 1,002 Н·с/м²,

для глицерина = 1480 Н·с/м².

Оценим, при какой скорости v* для падающего вертикально шара сила сопротивления сравняется с силой тяжести и движение станет равномерным.

Имеем

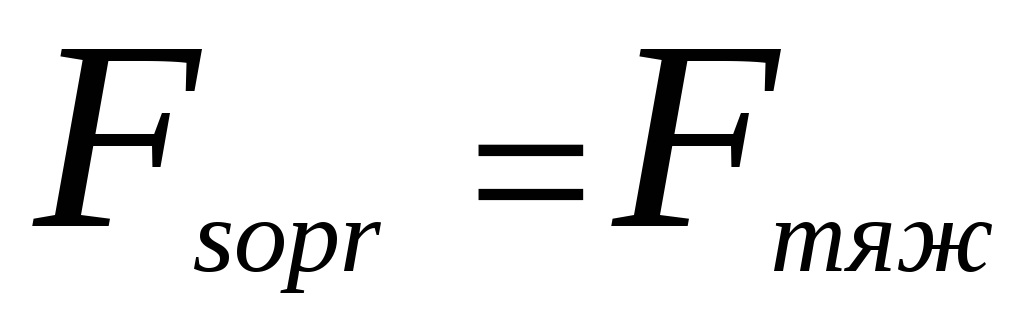
тогда

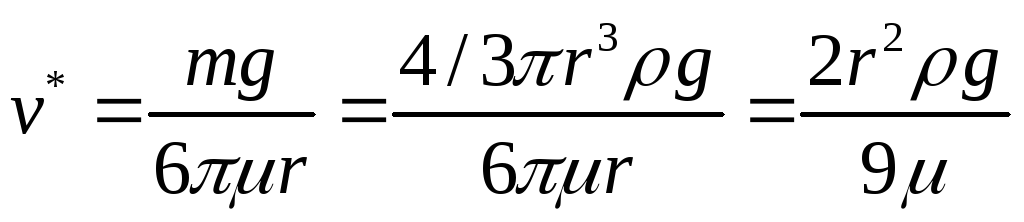
(6)

Пусть r = 0,1 м, = 0,8*10³ кг/м³ (дерево). При падении:

в воздухе v* = 960 м/с,

в воде v* = 17 м/с,

в глицерине v* = 0,012 м/с.

На самом деле первые два результата для v* не соответствуют действительности. Дело в том, что даже при меньших, чем первые две, скоростях становится пропорциональной квадрату скорости: .

Если квадратичная составляющая скорости намного больше линейной составляющей скорости в формуле: ,

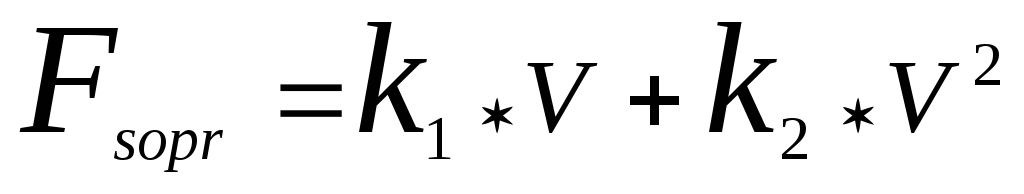т. е. k₂ v² » k₁v, то вкладом линейной составляющей k₁v можно пренебречь – это конкретный пример ранжирования параметров.

Определим значение коэффициента k₂. Величина k₂ пропорциональна площади сечения тела S, поперечного по отношению к потоку, плотности среды изависит от формы тела. Обычно представляют , где c - коэффициент лобового сопротивления - безразмерен. Некоторые значения c приведены на рис.1.

	Диск	с = 1,11
	Полусфера	с = 1,33
	Полусфера	с = 0,55
	Шар	с = 0,4
	Каплевидное тело	с = 0,045
	Каплевидное тело	с = 0,1