Файл: ОЗО-лекции комп мм.doc

в воде – =1*10³ кг/м³,

в глицерине – =1,26*10³ кг/ м³.

Используя квадратичную составляющую скорости при подсчете , можно получить v*: в воздухе v* = 18  м/с,

в воде v* = 0,65 м/с,

что соответствует действительности.

Свободное падение тела.

Математическая модель свободного падения тела – уравнение второго закона Ньютона с учетом двух сил, действующих на тело – силы тяжести и силы сопротивления среды : , где,.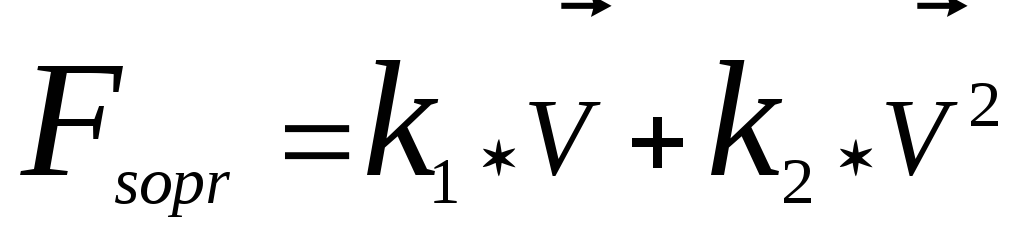

Движение является одномерным. Проецируя силу , скорость и перемещение на ось, направленную вертикально вниз, из (3) получаем

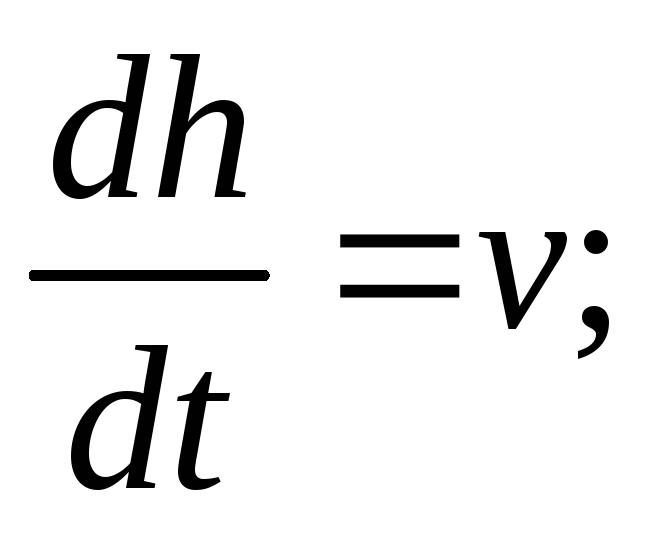
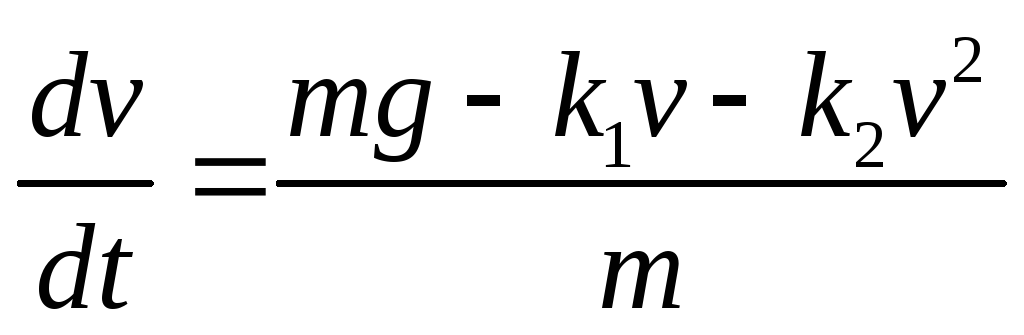(7)

В конкретных задачах можно одной из составляющих силы сопротивления пренебречь (если она заведомо много меньше другой).

Если скорость движения мала (v = 0.1 м/с), т. е. k₂ v² << k_1v, то отбрасывается квадратичная составляющая скорости в формуле силы сопротивления.

Если скорость движения велика (v =100 м/с),т. е. k₂ v² >> k _1v, то отбрасывается линейная составляющая скорости в формуле силы сопротивления.

Частичное тестирование моделирующей программы можно провести для движения без сопротивления. Аналитическое решение в этом случае общеизвестно.

---

Входные параметры модели:

• Начальная высота тела;

• Начальная скорость тела;

• Величины, определяющие коэффициенты сопротивления среды .

Задача

Парашютист совершает затяжной прыжок. Считая массу парашютиста заданной (m=80 кг), определить, начиная с какого времени после начала полета скорость человека - «безпарашютиста» становится постоянной. Построить график зависимости скорости падения «безпарашютиста» от времени.

Решение.

Нужно определить характер изменения скорости со временем, если все параметры, входящие в уравнения системы (7), заданы. При такой постановке модель носит дескриптивный характер. Ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений (7), однако, поскольку нужен график изменения скорости, то будем рассматривать только второе уравнение системы (7).

Поставим вопрос: влияет ли на полет «безпарашютиста» линейная составляющая скорости в ?

Скорость движения достаточно большая, поэтому вкладом линейной составляющей силы сопротивления k_1v можно пренебречь. Тогда получим систему дифференциальных уравнений:

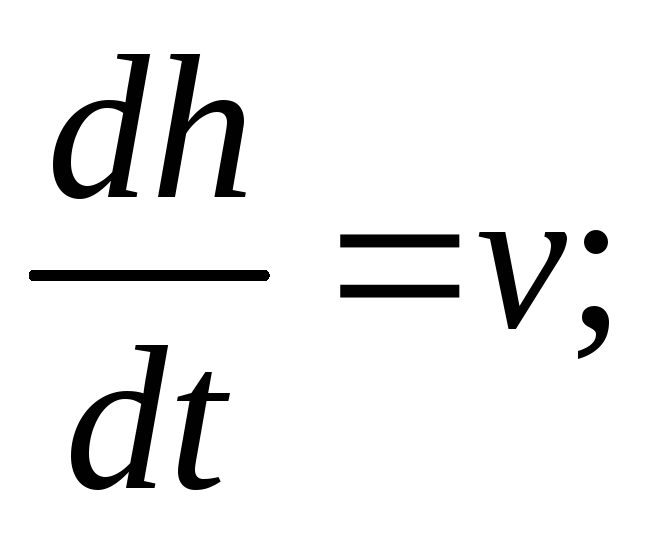
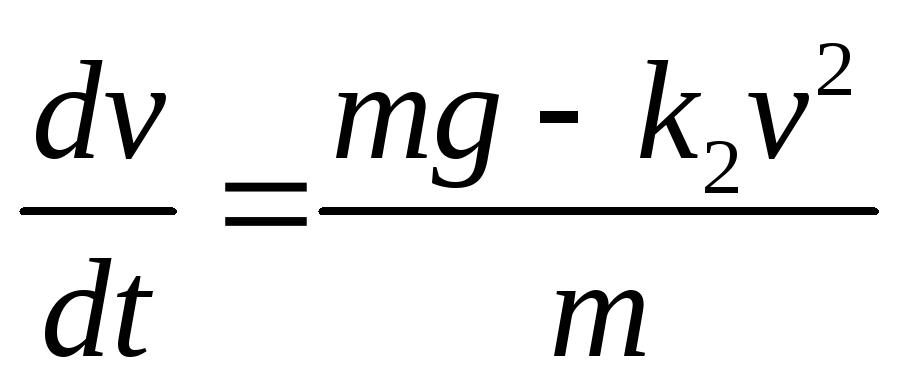(8)

;

из которых будем рассматривать только второе уравнение. Здесь v –скорость, t – время, h – высота, m – масса, g – ускорение свободного падения, k₂ – коэффициент квадратичной составляющей скорости.

Вычислим значение коэффициента k₂ для данной задачи. Средний рост человека возьмем средний - 1,7 м, а полуобхват грудной клетки –характерный размер – это приблизительно 0,4 м. Выберем число с = 1,22 как среднее между коэффициентами для диска и для полусферы (выбор для качественной оценки правдоподобен). Оценим площадь поперечного сечения:

S = 1,70,4=0,7 м².

= 1,29 кг/м³

---

Тогда 0,51,220,71,29 = 0.55083 кг/м.

Масса парашютиста m = 80 кг.

Теперь можно приступить к численному решению задачи. При этом следует воспользоваться одним из известных численных методов интегрирования систем обыкновенных дифференциальных уравнений. Решение находится с помощью, так называемого, исправленного метода Эйлера – метода Эйлера - Коши.

Метод ЭЙЛЕРА-КОШИ

В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Пусть дано уравнение

(9)

с начальным условием

.(10)

Выбрав достаточно малый шаг h, построим, начиная с точки х₀, систему равностоящих точек .Вместо искомой

интегральной кривой на отрезке рассмотрим отрезок касательной к ней в точке (обозначим ее L₁) с уравнением

При из уравнения касательнойполучаем:, откуда видно, что приращение значения функции на первом шаге имеет вид: _.

Аналогично, проводя касательную некоторой интегральнойкривой семейства в точке, получим:

что при дает т. е. получается из

---

добавлением приращения

Таким образом, получение таблицы значений искомой функции по методу Эйлера заключается в циклическом применении пары формул:

(11)

Существуют различные уточнения метода Эйлера, повышающие его точность. Модификации метода обычно направлены на то, чтобы более точно определить направление перехода из точки точку . Метод Эйлера - Коши, например, рекомендует следующий порядок вычислений:

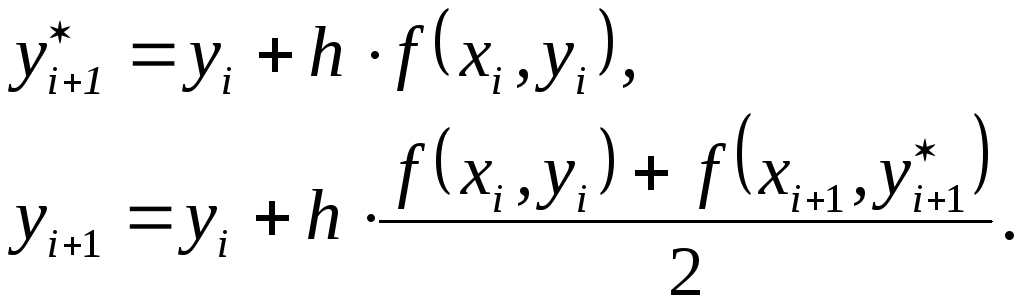(12)

Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке и во вспомогательнойточке, а в качестве окончательного берем среднее этих направлений.

В соответствии с методом Эйлера – Коши запишем итерационные уравнения нахождения значения скорости _i+1 в следующий момент времени из предыдущего _i (обозначим  – шаг по времени).Обозначив

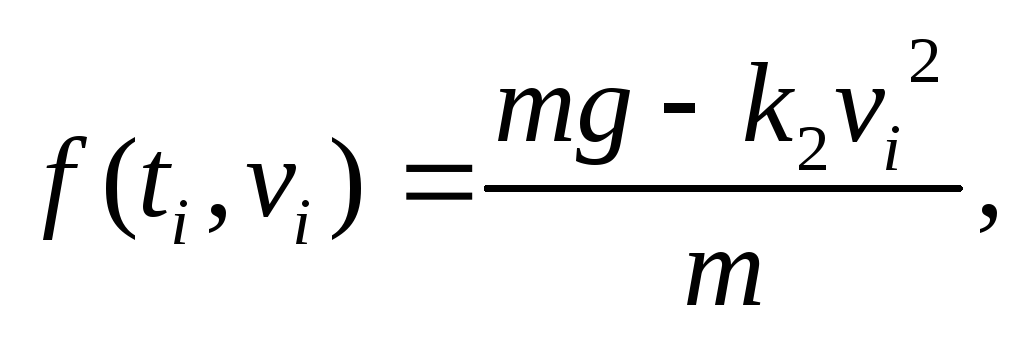(13)

Тогда в момент времени t_i+1 согласно методу Эйлера – Коши запишем формулы:

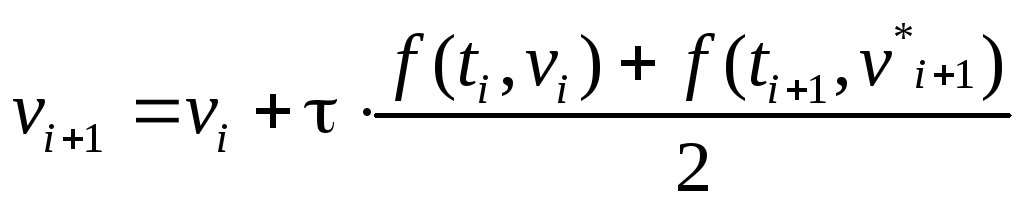(14)

Тогда, подставляя (13) в формулы (14), в итоге получим:

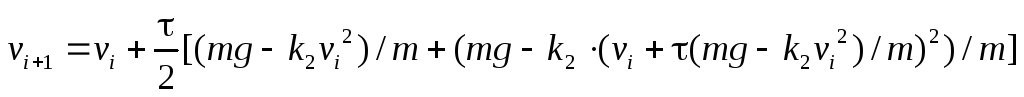
Для ускорения процесса работы над задачей целесообразно вместо составления программы воспользоваться готовой прикладной программой (например, табличным процессором Excel).

В Excel в ячейках D2, D4, D6, D8 таблицы будем хранить соответственно значения шага вычислений , массы «безпарашютиста» m, величины mg, коэффициента .Это связано с тем, что все константы удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать расчетные формулы Тогда для вычисления значения в ячейке В4 нужно записать формулу:

---

=B3+$D$2/2*(($D$6-$D$8*B3^2)/$D$4+($D$6-

$D$8*(B3+$D$2*($D$6-$D$8*B3^2)/$D$4)^2)/$D$4)

и произвести автозаполнение столбца В.

В столбце А в ячейку А4 нужно записать формулу: =СУММ(А3;$D$2) и произвести автозаполнение столбца А.

Построение графика .

1. Выделить диапазон ячеек B3:B20, содержащий данные для построения графика. Значения из столбца A (диапазон A3:A20) будут откладываться по оси ОХ (ось времени), значения из столбца B (диапазон B3:B20) – по оси OY.

2. Выбрать команду Вставка, Диаграмма. С помощью мастера диаграмм провести построение графика в четыре этапа (шага).

Шаг 1.

• В диалоговом окне Тип диаграммы на вкладке Стандартные выбрать тип диаграммы Точечная и вид – Точечная диаграмма со значениями, соединенными сглаживающими линиями.

• Щелкнуть на кнопке Далее.

Шаг 2.

• В окне Источник данных диаграммы на вкладке Диапазон данных проверить, что диапазон данных выбран правильно и установлен флажок опции Ряды в столбцах.

• Выбрать вкладку Ряд и в поле Имя: ввести название графика Зависимость v от t.

• Установить курсор в поле «Подписи оси Х» и занести диапазон ячеек по переменной t (1 столбец).

• Щелкнуть на кнопке Далее.

Шаг 3.

На этом шаге задаются параметры диаграммы (окно Параметры диаграммы).

> На вкладке Заголовки ввести название диаграммы и наименования осей координат с указанием единиц измерения величин, откладываемых по этим осям:

• в поле Название диаграммы — График зависимости v от t;

• в поле Ось X (категорий) — Время t, (с);

в поле Ось Y (значений) — Скорость v, (м/c).

Результаты вычислений, выполненных в табличном процессоре:

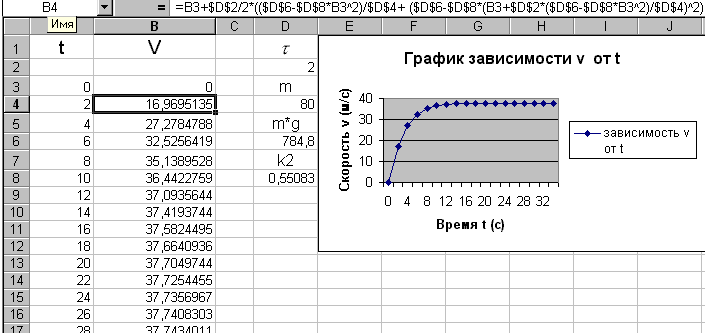
Учтем, что  для разных задач нужно выбирать индивидуально. Если в задаче о безпарашютисте можно  взять равным 2 сек., то в задаче о парашютисте  равно 0.2 сек, т.к. скорость меньше.

---