ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 21.08.2024
Просмотров: 20
Скачиваний: 1
|
1.Линейная электрическая цепь и её элементы. Если зависимость U(I) или I(U) какого-либо элемента электрической цепи линейна, то такой элемент называют линейным, а электрическую цепь, состоящую только из линейных элементов - линейной цепью. Электрическая цепь является нелинейной, если она содержит хотя бы один нелинейный элемент. Для линейного элемента справедливо U=rI или I=gU. Эл ты: Сопротивление (резистор), Ёмкость (конденсатор), Индуктивность (катушка) 2.Св-ва, хар-ки и услов. обознач. эл-ов. Режимы работы цепей. Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. В
простейшем случае проводника длиной
и сечением S его сопротивление
определяется выражением
Сопротивление пассивного участка цепи в общем случае определяется по формуле
где P - потребляемая мощность;I - ток. Катушка – это пассивный элемент, характеризующийся индуктивностью. Индуктивностью называется идеальный элемент схемы замещения, характеризующий способность цепи накапливать магнитное поле. Полагают, что индуктивностью обладают только индуктивные катушки. Индуктивностью других элементов электрической цепи пренебрегают. Индуктивность катушки, измеряемая в генри [Гн], определяется по формуле
где W - число витков катушки; Ф - магнитный поток катушки, возбуждаемый током i. Конденсатор – это пассивный элемент, характеризующийся емкостью. Емкостью называется идеальный элемент схемы замещения, характеризующий способность участка электрической цепи накапливать электрическое поле. Полагают, что емкостью обладают только конденсаторы. Емкостью остальных элементов цепи пренебрегают. Емкость конденсатора, измеряемая в фарадах (Ф), определяется по формуле:
где q - заряд на обкладках конденсатора;Uс - напряжение на конденсаторе. В зависимости от нагрузки различают следующие режимы работы: номинальный, режим холостого хода, короткого замыкания, согласованный режим. При номинальном режиме электротехнические устройства работают в условиях, указанных в паспортных данных завода-изготовителя. В нормальных условиях величины тока, напряжения, мощности не превышают указанных значений. Режим холостого хода возникает при обрыве цепи или отключении сопротивления нагрузки. Режим короткого замыкания получается при сопротивлении нагрузки, равном нулю. Ток короткого замыкания в несколько раз превышает номинальный ток. Режим короткого замыкания является аварийным. Согласованный режим - это режим передачи от источника к сопротивлению нагрузки наибольшей мощности. Согласованный режим наступает тогда, когда сопротивление нагрузки становится равным внутреннему сопротивлению источника. При этом в нагрузке выделяется максимальная мощность. 3.Основные понятия.Законы Ома,Дж.Ленца и Кирхгофа при анализе цепей. Ток,
протекающий через сопротивление R,
пропорционален падению напряжения
на сопротивлении и обратно пропорционален
величине этого сопротивл
11. Особенности расчёта нелинейных электрических цепей. Общих методов расчета нелинейных цепей не существует. Известные приемы и способы имеют различные возможности и области применения. В общем случае при анализе нелинейной цепи описывающая ее система нелинейных уравнений может быть решена следующими методами: графическими; аналитическими; графо-аналитическими; итерационными. Графические методы расчета При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями. Метод двух узлов Д
Рассмотрим схему, содержащую всего 2 узла. Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое принимают напряжение между двумя узлами схемы. In=(En – Uab)gn. Ток к узлу а и b не подтекает. Поэтому если принять I=0, то Uab=(ΣEk gk + ΣIk)/Σgk – напряжение. После этого можно найти ток в любой ветви: In=(En – Uab)gn. 12.Генерирование синусоидальной Э.Д.С. В линейных электрических цепях синусоидальный ток возникает под действием синусоидальной Э.Д.С. Синусоидальную зависимость можно получить, вращая с постоянной скоростью в равномерном магнитном поле проводник в виде прямоугольной рамки площадью S. Тогда магнитный поток через рамку
Поскольку
при равномерном вращении рамки угловая
скорость
Так как при вращении рамки пересекающий её магнитный поток всё время меняется, то по закону электромагнитной индукции в ней будет наводиться Э.Д.С. индукции
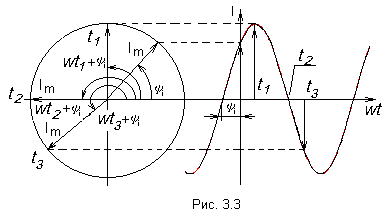
где Е0 – амплитуда синусоидальной Э.Д.С. 13. Аналитическое и графическое представление синусоидальных величин. В
электротехнике наибольшее распространение
получил синусоидальный перем ток, то
есть ток, величина которого изменяется
по закону синуса. Поэтому мгновенное
значение синусоидального тока
выражается формулой ω
– угловая частота (выражается в рад/с
или с-1 ).
19.Взаимоиндукция Е
На
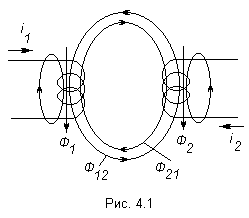
(рис. 4.1) показаны две катушки с
числом витков
Аналогично магнитный поток второй катушки пронизывает витки первой. Такие катушки называются индуктивно – связанными (или магнитно-связанными). Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи k, который определяется отношением:
где М - взаимная индуктивность элементов цепи, Гн.
Необходимо запомнить, что коэффициент связи не может быть больше единицы! Вообще,
взаимной индуктивностью первой
и второй катушек называется отношение
добавочного потокосцепления второй
катушки
Индекс 12 показывает, что взаимная индуктивность наводится в первой катушке от действия магнитного потока второй катушки. Опыт
показывает, что:
Справедливо соотношение:
Взаимная индуктивность в линейных электрических цепях не зависит от направлений и значений токов, и определяется только конструкцией катушек их взаимным расположением. Об этом также свидетельствует выражение (4.5). Индуктивность катушки определяется по формуле:
где
S – площадь поперечного сечения катушки, мм2; L - длина катушки , м.
23. Основные схемы соединения трёхфазных цепей
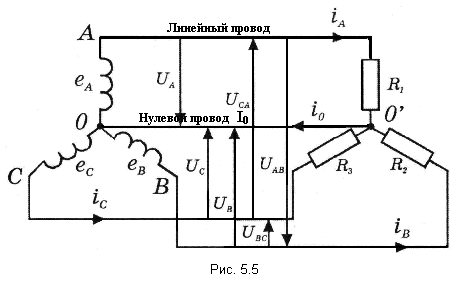
Существуют различные способы соединения обмоток генератора с нагрузкой, но в целях экономии обмотки трёхфазного генератора соединяют в звезду или в треугольник. П Ниже приведены схемы соединения трёхфазного генератора с трёхфазной нагрузкой по схеме звезда: звезда с нулевым проводом (рис.5.5); звезда без нулевого провода (рис. 5.6). Т Провода, соединяющие точки А, В, С генератора с точками а,b,с нагрузки, называют линейными. Нулевым проводом называют провод, соединяющий нулевые точки генератора и нагрузки Линейными
токами Iл называют
токи текущего линейным проводам (их
обозначают
Фазным
напряжением Uф называют
напряжение между началом и концом
фазы или между линейным и нулевым
проводом (их обозначают
Линейным
напряжением UЛ называют
напряжение между двумя линейными
проводами ( их обозначают
Фазные
и линейные напряжения связаны между
собой выражениями В симметричной системе фазных напряжений система линейных напряжений
тоже симметрична:
и Действующее значение линейных напряжений легко определяется по векторной диаграмме (рис.5.7) из треугольника, например АОВ:
Таким образом, получим общее соотношение между линейными и фазными напряжениями в симметричной системе
При соединении звездой в точках перехода из генератора в линию и из линии в нагрузку нет разветвлений, поэтому фазные и линейные токи одинаковы между собой в каждой фазе:
Запомните:
соотношения
П
2 Соотношения между фазными и линейными токами легко можно определить, если для каждой узловой точки применить первый закон Кирхгофа:
При симметричной нагрузке токи во всех фазах одинаковы: линейные токи сдвинуты относительно фазных токов на 900 (рис. 5.10). Д
Таким образом, получим общее соотношение между линейными и фазными токами
Из схемы (рис.5.9) видно, что фазные и линейные напряжения совпадают:
Запомните:
соотношения
|
Падением напряжения на сопротивлении называется произведение тока, протекающего через сопротивление, на величину этого сопротивления. Основными законами электрических цепей, наряду с законом Ома, являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа). В соответствии с первым законом Кирхгофа, алгебраическая сумма токов в любом узле цепи равна нулю:
запишем
уравнение по первому закону Кирхгофа.
Токам, направленным к узлу, присвоим знак "плюс",а токам, направленным от узла - знак "минус". С Согласно
закону Джоуля-Ленца, вся электрическая
энергия, сообщаемая проводнику в
результате работы сил электрического
поля, превращается в тепловую энергию.
С помощью закона Ома можно записать
для потребителя с сопротивлением R:
Обычно под законом Джоуля-Ленца понимают уравнение, определяющее не энергию, а мощность тепловых потерь
В приведенных выражениях тепловая энергия и мощность выражаются в Джоулях [Дж] и Ваттах [Вт] соответственно. 4.Эквивалентность групп сопротивлений в линейных электрических цепях. При последовательном соединении роль эквивалентного сопротивления (или сопротивления эквивалентного потребителя) играет сумма сопротивлений всех потребителей (рис. 1.11.).
Это следует из II закона Кирхгофа:
При двух последовательно соединенных потребитлях:
При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
Это следует из I закона Кирхгофа:
При двух параллельно соединенных потребителях Т
14. Последовательное соединение элементов R, L, C в цепи синусоидального напряжения
В Все законы постоянного тока справедливы и для синусоидального, только записанные в комплексной форме. Вектор напряжения на входе равен сумме векторов напряжений на элементах R, L, C:
По закону Ома можно расписать:
Отсюда
Значит полное сопротивление для цепи на рис. 3.11
где
Можно рассмотреть три случая значений:
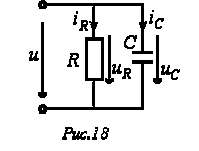
15. Парралельное соединение R, L, C . Параллельное соединение резистивного и емкостного элементов
Для цепи на рис. 18 имеют место соотношения:
Параллельное соединение резистивного и индуктивного элементов
Для цепи на рис. 21 можно записать
.
20.Последовательное соединение индуктивно связанных элементов цепи
Д
При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов, поэтому магнитные потоки самоиндукции Ф11 (или Ф22) и взаимной индукции Ф12 (или Ф21), сцепленные с каждым элементом, складываются. При встречном включении токи в обоих элементах цепи в любой момент времени направлены противоположно относительно одноименных выводов, поэтому магнитные потоки самоиндукции и взаимной индукции, сцепленные с каждым элементом, вычитаются. Индуктивность двух последовательно соединенных индуктивно связанных элементов определяется выражением:
где
Знак плюс относится к согласному, а знак минус ко встречному включению. Следовательно, L = L1 + L2 ± 2M. Полное сопротивление при согласном включении больше, чем при встречном. Напряжения на элементах имеют по три составляющие:
Если индуктивность одного из элементов меньше взаимной индуктивности, то при встречном включении наблюдается своеобразный «емкостный» эффект. Пусть, например, L2 < М, при этом в выражении
имеем
ω(L2-M) < 0, и, следовательно,
напряжение
24. Законы Ома и Кирхгофа в комплексной форме Уравнение 3.9 представляет собой закон Ома для цепи синусоидального тока в комплексной форме
где Z – комплексное сопротивление, Ом. В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть jX,
По
первому закону Кирхгофа, алгебраическая
сумма мгновенных значений токов,
сходящихся в любом узле схемы равна
нулю:
Подставив
вместо
Уравнение 3.11 представляет первый закон Кирхгофа в комплексной форме.
Для
замкнутого контура сколь угодно
сложной электрической цепи синусоидального
тока можно составить уравнение по
второму закону Кирхгофа и представить
в комплексной форме:
|
5 Значительно упрощают расчет методом контурных токов, так как он позволяет сократить число уравнений. При расчёте этим методом полагают, что в каждом независимом контуре схемы течёт свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей. Метод наложения: ток в любой ветви равен алгебраической сумме токов, вызываемых каждой из Э.Д.С. схемы в отдельности. Линейная электрическая цепь описывается системой линейных уравнений Кирхгофа. Это означает, что она подчиняется принципу наложения (суперпозиции), согласно которому совместное действие всех источников в электрической цепи совпадает с суммой действий каждого из них в отдельности. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по I закону Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, – один из основных расчетных методов. В том случае, когда п-1 < p (n – количество узлов, p – количество независимых контуров), данный метод более экономичен, чем метод контурных токов. 6. Причины возникновения и сущность переходных процессов. Переход из одного стационарного состояния в другое происходит не мгновенно, а с течением времени, что обусловлено наличием в цепи накопителей энергии (индуктивностей катушек и ёмкостей конденсаторов). Магнитная энергия катушек и электрическая энергия конденсаторов скачком измениться не могут, т.к. для осуществления этого необходимы источники, имеющие бесконечно большую мощность. Процессы, сопровождающие этот переход, называются переходными. 7. Анализ переходных процессов во временной области. Классический метод Классический метод расчета переходных процессов основан на составлении и последующем решении (интегрировании) дифференциальных уравнений, составленных по законам Кирхгофа и связывающих искомые токи и напряжения послекоммутационной цепи и заданные воздействующие функции (источники электрической энергии. Преобразуя систему уравнений, можно вывести итоговое дифференциальное уравнение относительно какой-либо одной переменной величины x(t): Здесь n – порядок дифференциального уравнения, он же – порядок цепи, коэффициенты ak > 0 и определяются параметрами пассивных элементов R, L, C цепи, а правая часть является функцией задающих воздействий. В соответствии с классической теорией дифференциальных уравнений полное решение неоднородного дифференциального уравнения находится в виде суммы частного решения неоднородного дифференциального уравнения и общего решения однородного дифференциального уравнения: Ч Общее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части. Таким образом, любая искомая величина в переходном режиме
16.Активное реактивное и полное сопротивления. Треугольник сопротивлений
Из этого следует, что модуль комплексного сопротивления:
С При этом
Зная
Знак
угла
17.Резонанс напряжений. Коэфф. Мощности. Треугольник мощностей. Соответствует
случаю, когда
Из формулы 3.41 можно сделать вывод, что мощности P, Q, S связаны следующей зависимостью:
Г
Отношение
Р к S, равное
На
практике всегда стремятся увеличить
21.Параллельное соединение индуктивно связанных элементов цепи
Две катушки с сопротивлениями R1 и R2, индуктивностями L1 и L2 и взаимной индуктивностью М соединены параллельно, причем одноимённые выводы присоединены к одному и тому же узлу (рис. 4.7).
При выбранных положительных направлениях токов и напряжения получаем следующие выражения:
где
В
этих уравнениях комплексные напряжения
Откуда следует, что входное комплексное сопротивление рассматриваемой цепи
Рассмотрим
теперь включение, при котором одноименные
выводы присоединены к разным узлам,
т. е. L1 и L2 присоединены к
узлу разноименными выводами. В этом
случае положительные направления
напряжений взаимной индукции (выбранные
сверху вниз) и тех токов, от которых
они зависят, ориентированы относительно
одноименных выводов неодинаково и
комплексные напряжения
25.Определение четырёхполюсника. Основные формы записи уравнений четырёхполюсника
В ряде случаев необходимо рассматривать электрические цепи с двумя входными и двумя выходными зажимами, в которых ток и напряжение на входе связаны линейными зависимостями с напряжением и током на выходе. Такие цепи называются четырёхполюсниками. Они могут иметь сколь угодно сложную структуру, так как в процессе исследования цепи важно определить не токи и напряжения в отдельных ветвях, а только зависимости между входными и выходными напряжениями и токами. Иногда четырёхполюсниками называют электрические аппараты и устройства, имеющие пару входных и пару выходных зажимов. К ним, например, относятся однофазные трансформаторы, участки линии электропередачи, мостовые диодные выпрямители, сглаживающие фильтры и прочее. Условное изображение четырехполюсника показано на рис. 7.1. О Если четырёхполюсник не содержит источников электрической энергии, то он называется пассивным, а если содержит – активным. Примером активного четырёхполюсника может служить электронный усилитель. На схеме активный четырёхполюсник изображается в виде прямоугольника с буквой А. Пассивный четырёхполюсник обозначается буквой П, либо вообще не обозначается. Если у четырёхполюсника рабочими являются обе пары зажимов, то он называется проходным. Четырёхполюсник,
по сути, является передаточным звеном
между источником питания и нагрузкой.
К входным зажимам
Зависимости между двумя напряжениями и двумя токами на входных и выходных выводах можно записать в различной форме. Если считать две из указанных величин заданными, то две другие величины будут связаны с ними системой двух уравнений, которые называются уравнениями четырёхполюсника. Возможны следующие шесть форм записи уравнений пассивного четырёхполюсника: Форма А (основная):
где A,D – безразмерные коэффициенты; B – [Ом] С – [См]= [Ом-1]
27. Метод эквивалентного генератора
В При расчёте сложной электрической цепи приходится выполнять значительную вычислительную работу даже в том случае, когда требуется определить ток в одной ветви. Объём этой работы в несколько раз увеличивается, если необходимо установить изменение тока, напряжения, мощности при изменении сопротивления данной ветви, так как вычисления нужно производить несколько раз, задаваясь различными значениями сопротивления. В любой электрической схеме можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от структуры и сложности, условно изобразить прямоугольником, который представляет собой так называемый двухполюсник. Таким образом, двухполюсник - это обобщённое название схемы, которая двумя выходными зажимами (полюсами) присоединена к выделенной ветви. Если в двухполюснике есть источник Э.Д.С. или тока, то такой двухполюсник называют активным. Если в двухполюснике нет источника Э.Д.С. или тока, то его называют пассивным. При решении задачи методом эквивалентного генератора (активного двухполюсника) необходимо:
1
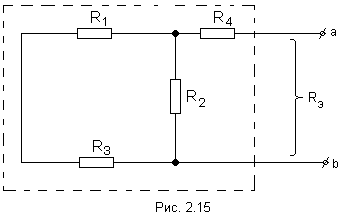
Напряжение
холостого хода Uо (эквивалентное Э.Д.С.
Еэ) для рассматриваемой цепи можно
найти так: Сопротивление R4 в расчёт не вошло, так как при разомкнутой ветви ab ток по нему не протекает. 3. Найти эквивалентное сопротивление. При этом источники Э.Д.С. закорачиваются, а ветви, содержащие источники тока, размыкаются. Двухполюсник становится пассивным.
Д
4. Вычислить
значение тока. Для данной схемы имеем:
|
8. Анализ переходных процессов во временной области. операторный метод. Идея
операторного метода заключается в
замене вещественной переменной t
комплексной переменной
Подобный прием применялся при анализе стационарного решения цепей символическим методом. Однако в то время, как символический метод можно применять лишь к гармоническим функциям, операторный метод обладает значительно большей общностью и применим к широкому классу функций.
9. Исследование переходных процессов при помощи интеграла Дюамеля.
Последовательность
расчета с использованием
интеграла
Дюамеля. О Запись
выражения
Определение
производной
Подстановка найденных функций в (1) и интегрирование определенного интеграла. В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения. Исходные
данные для расчета:
Переходная проводимость
Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения. 10. Нелинейные электрические цепи постоянного тока. Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент. Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками. Нелинейные элементы можно разделить на двух – и многополюсные. Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи.
18.Мгновенная и средняя мощности. Активная, реактивная и полная мощности. Измерение мощности ваттметром
Если имеются законы изменения тока и напряжения
то их произведение
Мгновенная мощность
График этой функции - результат графического умножения графиков тока и напряжения. Под активной мощностью Р понимают среднее значение мгновенной мощности за период Т:
Учитывая соотношения можно записать
Активная
мощность физически представляет
собой энергию, которая выделяется в
единицу времени в виде теплоты на
участке цепи с сопротивлением R.
Действительно, произведение
Единица активной мощности - 1Вт (Ватт).
Под реактивной мощностью Q принимают произведение напряжения на участке цепи на ток, протекающий по этому участку, и на синус угла φ между напряжением и током.
Единица реактивной мощности – вольт-ампер реактивный (ВАр). Величина, объединяющая активные реактивные мощности, называется полной мощностью.
Единица полной мощности - вольт-ампер (ВА). Для того, чтобы вычислить полную мощность нужно комплекс напряжения умножить на сопряженный комплекс тока:
Можно расписать
Таким
образом, активная мощность Р есть
действительная часть (Re),
а реактивная Q - мнимая
часть (Im) произведения
22.Трёхфазные цепи.Общее.. Объединение в одной линии электропередачи нескольких цепей переменного тока с независимыми источниками электроэнергии называется многофазной системой. Наибольшее распространение получила трёхфазная система, которая была изобретена и разработана выдающимся русским инженером М. О. Доливо-Добровольским в 1889-1891гг. Трёхфазной симметричной системой Э.Д.С. называется совокупность трёх Э.Д.С. одинаковой частоты и амплитуды, сдвинутых друг относительно друга по фазе на 1200 . Эти три Э.Д.С. можно изобразить на временной (рис.5.1) и векторной (рис. 5.2.) диаграммах. Трёхфазные симметричные системы Э.Д.С. получаются с помощью трёхфазного генератора, в котором имеются три самостоятельные обмотки, расположенные на статоре, и сдвинутые относительно друг друга в пространстве на 1200. В центре статора вращается магнит (рис. 5.3). Форма магнита такова, что магнитный поток, пронизывающий каждую катушку, изменяется по синусоидальному закону. Тогда по закону электромагнитной индукции в катушках будут индуцироватьсяЭ.Д.С.равной амплитуды и частоты, отличающиеся друг от друга на 1200 .
Комплексы действующих значений этих Э.Д.С.:
Следующий
порядок чередования Э.Д.С.
В дальнейшем при рассмотрении трёхфазных систем принимается прямая последовательность фаз, которая считается нормальной.
26.Эквивалентные схемы четырёхполюсника
Для пассивных четырёхполюсников чаще выбирают Т- или П- образную схему замещения, состоящую из трёх независимых элементов. Иногда применяют мостовую (Х образную) схему замещения. Т Значения трёх сопротивлений этих схем определяют с учетом того, что схема замещения должна обладать теми же коэффициентами A, B, C, D, что и заданный четырехполюсник. Т- образная схема (схема звезды) Для этой схемы справедливы следующие соотношения:
Подставив
значения
Сравнивая полученные уравнения 7.9 и 7.10 с системой уравнений формы А 7.1 и 7.2 записываем значения искомых величин:
П – образная схема (схема треугольника) А
Тогда можно записать искомые значения сопротивлений:
Если
четырёхполюсник симметричный, то в Т
– схеме
1.Линейная электрическая цепь и её элементы. 2.Св-ва, хар-ки и услов. обознач. эл-ов. Режимы работы цепей. 3.Основные понятия.Законы Ома,Дж.Ленца и Кирхгофа при анализе цепей. 4.Эквивалентность групп сопротивлений в линейных электрических цепях.
5 6. Причины возникновения и сущность переходных процессов. 7. Анализ переходных процессов во временной области. Классический метод 8. Анализ переходных процессов во временной области. операторный метод.
9. Исследование переходных процессов при помощи интеграла Дюамеля. 10. Нелинейные электрические цепи постоянного тока. 11. Особенности расчёта нелинейных электрических цепей. 12.Генерирование синусоидальной Э.Д.С 13. Аналитическое и графическое представление синусоидальных величин. 14. Последовательное соединение элементов R, L, C в цепи синусоидального напряжения 15. Парралельное соединение R, L, C 16.Активное реактивное и полное сопротивления. Треугольник сопротивлений 17.Резонанс напряжений. Коэфф. Мощности. Треугольник мощностей. 18.Мгновенная и средняя мощности. Активная, реактивная и полная мощности. Измерение мощности ваттметром 19.Взаимоиндукция 20.Последовательное соединение индуктивно связанных элементов цепи 21.Параллельное соединение индуктивно связанных элементов цепи 22.Трёхфазные цепи.Общее 23. Основные схемы соединения трёхфазных цепей 24. Законы Ома и Кирхгофа в комплексной форме 25.Определение четырёхполюсника. Основные формы записи уравнений четырёхполюсника 26.Эквивалентные схемы четырёхполюсника
27. Метод эквивалентного генератора
|
 сли
изменение тока в одном из элементов
электрической цепи приводит к
возникновению Э.Д.С. в другом элементе
цепи, то говорят, что эти элементы
индуктивно связаны друг с другом.
Возникающая при этом Э.Д.С. называется
Э.Д.С. взаимной индукции.
сли
изменение тока в одном из элементов
электрической цепи приводит к
возникновению Э.Д.С. в другом элементе
цепи, то говорят, что эти элементы
индуктивно связаны друг с другом.
Возникающая при этом Э.Д.С. называется
Э.Д.С. взаимной индукции.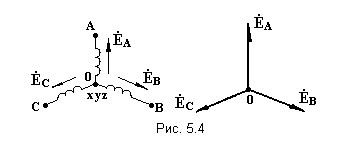
 ри
соединении в звезду концы обмоток
генератора объединяются в одну точку
О, которая называется нулевой, или
нейтральной (рис. 5.4).
ри
соединении в звезду концы обмоток
генератора объединяются в одну точку
О, которая называется нулевой, или
нейтральной (рис. 5.4).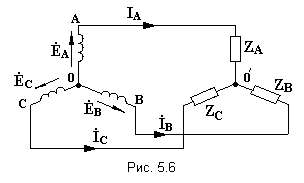 очку,
в которой объединяют три конца
трёхфазной нагрузки при соединении
её звездой, называют нулевой точкой
нагрузки и обозначают О’.
очку,
в которой объединяют три конца
трёхфазной нагрузки при соединении
её звездой, называют нулевой точкой
нагрузки и обозначают О’. .
(5.4)
.
(5.4)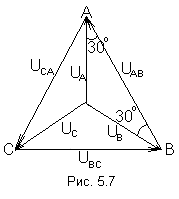 сдвинуты относительно друг друга на
1200 (рис. 5.7).
сдвинуты относительно друг друга на
1200 (рис. 5.7).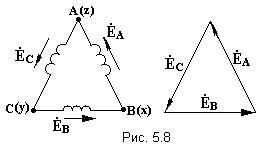 ри
соединении обмоток генератора
треугольником конец первой обмотки
генератора соединяют с началом второй,
конец второй с началом третьей, конец
третьей- с началом пеhвой.
(рис. 5.8)
ри
соединении обмоток генератора
треугольником конец первой обмотки
генератора соединяют с началом второй,
конец второй с началом третьей, конец
третьей- с началом пеhвой.
(рис. 5.8)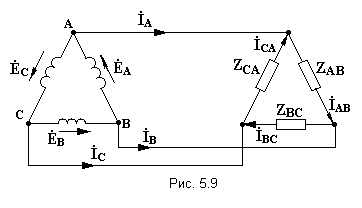 3.Геометрическая
сумма Э.Д.С. в замкнутом треугольнике
равна нулю (рис. 5.8). В отличие от
соединения звездой, где в большинстве
случаев применяется четырёхпроводная
система, здесь используется три провода
(рис. 5.9).
3.Геометрическая
сумма Э.Д.С. в замкнутом треугольнике
равна нулю (рис. 5.8). В отличие от
соединения звездой, где в большинстве
случаев применяется четырёхпроводная
система, здесь используется три провода
(рис. 5.9).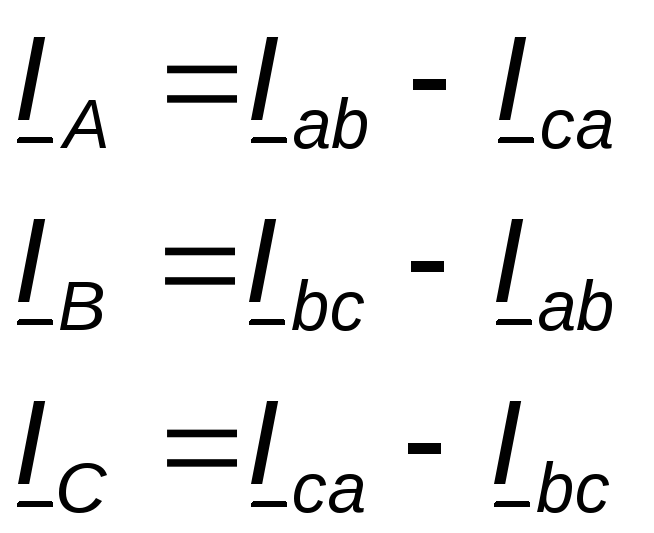 ;
(5.7)
;
(5.7)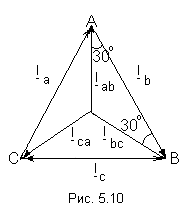 ействующее
значение линейных токов определяется
по векторной диаграмме (рис.5.10) из
треугольника, например АОС:
ействующее
значение линейных токов определяется
по векторной диаграмме (рис.5.10) из
треугольника, например АОС: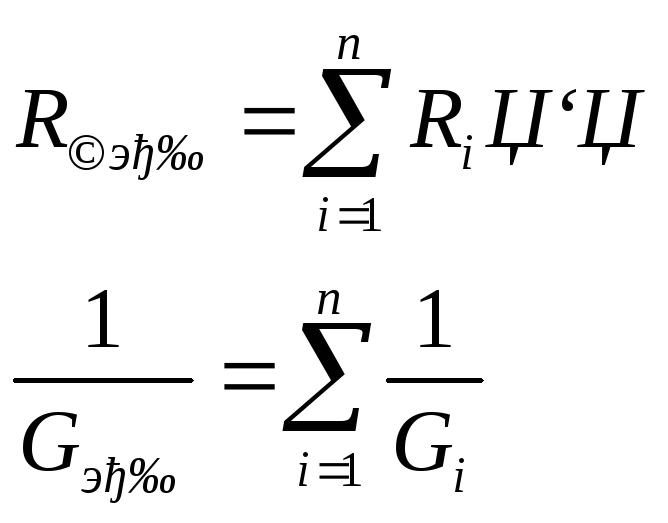
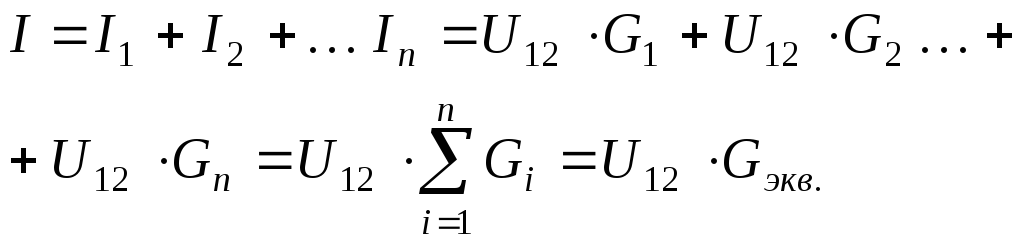
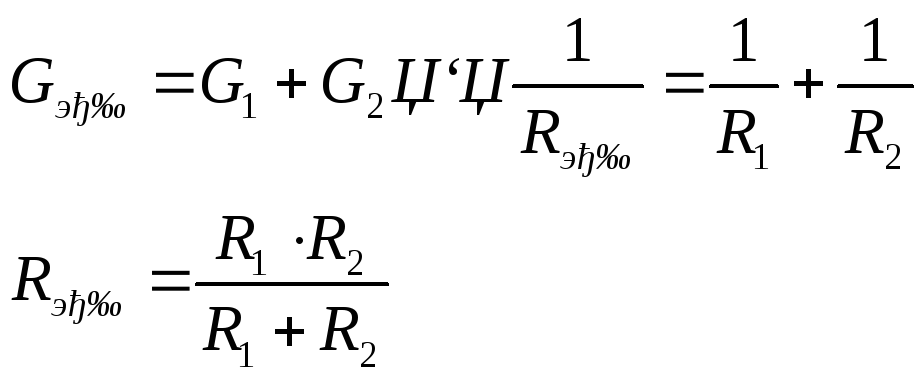 аким
образом, для расчета цепей с
последовательно включенными
потребителями целесообразно их
свойства выражать значениями
сопротивлений, а для параллельно
включенных – значениями проводимостей.
аким
образом, для расчета цепей с
последовательно включенными
потребителями целесообразно их
свойства выражать значениями
сопротивлений, а для параллельно
включенных – значениями проводимостей.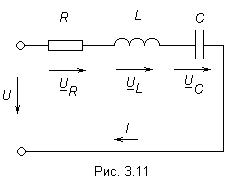 электрической цепи (рис. 3.11) элементы
R, L, C соединены последовательно и
подключены к источнику синусоидального
напряжения. Ток в такой цепи будет
изменяться также
по синусоидальному закону.
электрической цепи (рис. 3.11) элементы
R, L, C соединены последовательно и
подключены к источнику синусоидального
напряжения. Ток в такой цепи будет
изменяться также
по синусоидальному закону.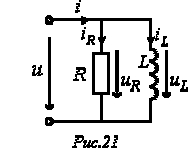 ;
; роводимость;
роводимость;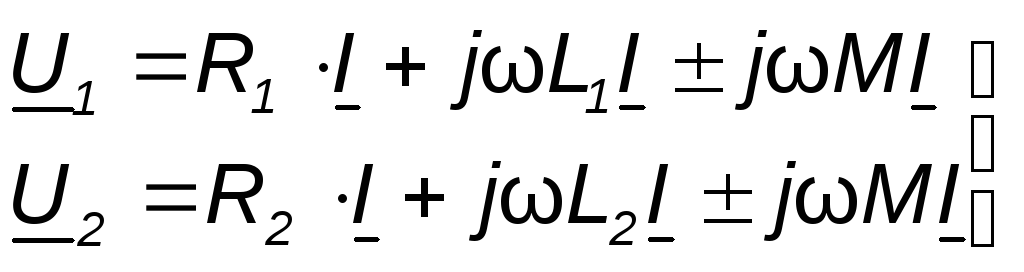 (4.8)
(4.8)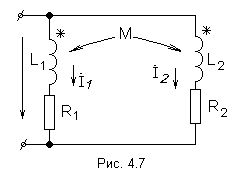
 (4.14)
(4.14)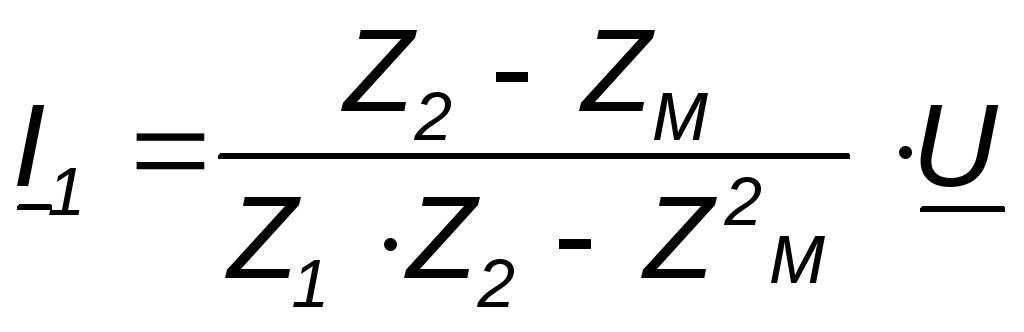 ;
(4.15)
;
(4.15)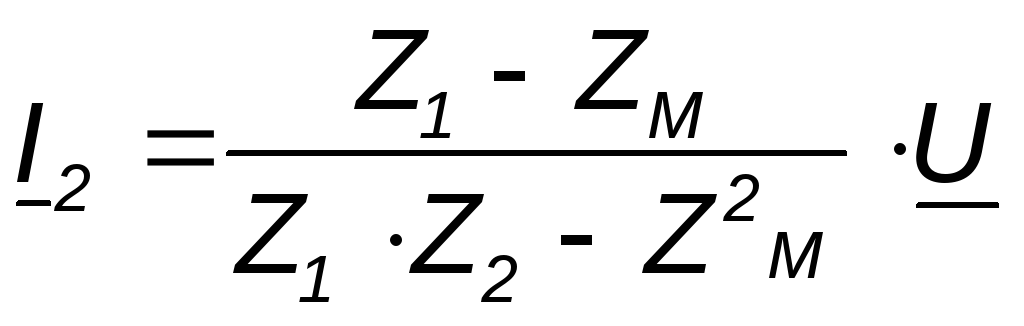 ;
(4.16)
;
(4.16)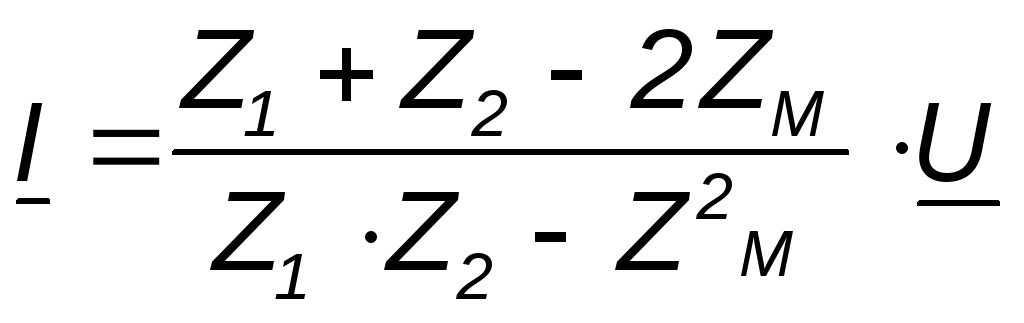 .
(4.17)
.
(4.17)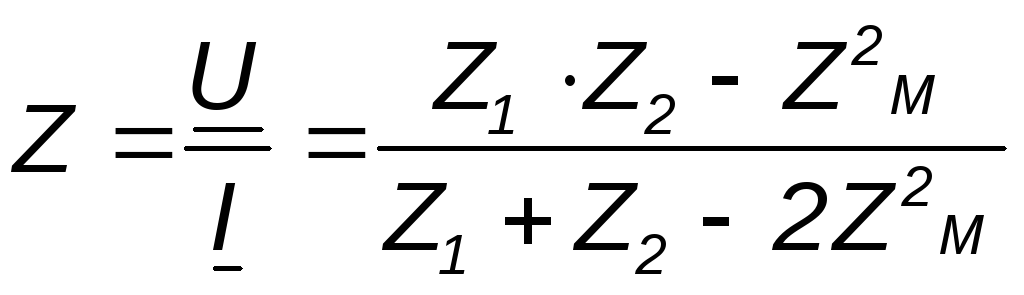 .
(4.18)
.
(4.18)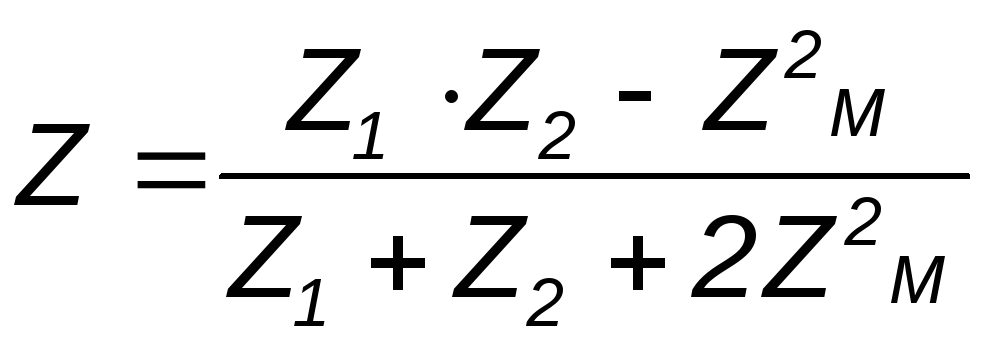 .
(4.19)
.
(4.19)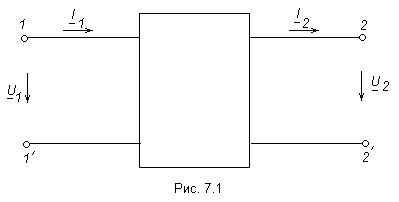 дну
пару выводов называют входными
(обозначаются
дну
пару выводов называют входными
(обозначаются
 ля
данной схемы
ля
данной схемы
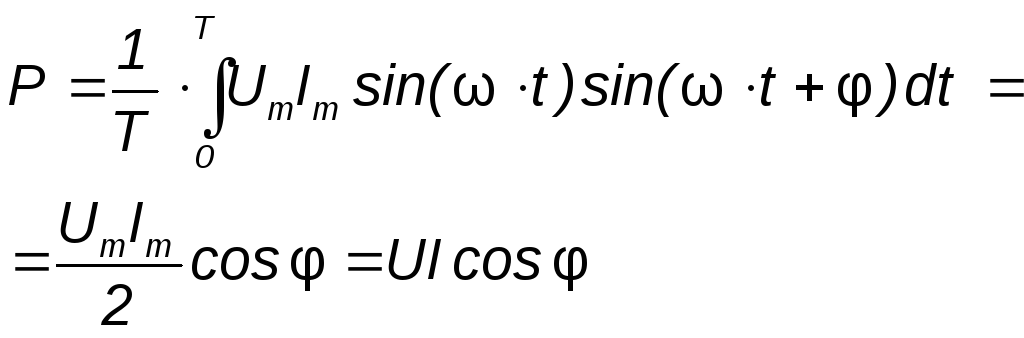
 (3.36)
(3.36)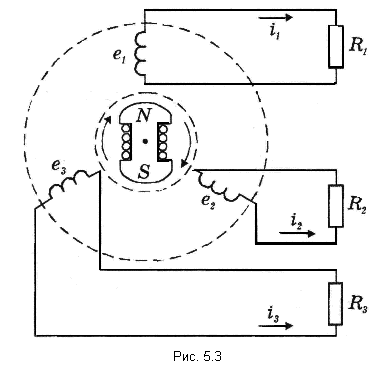 ;
(5.1)
;
(5.1)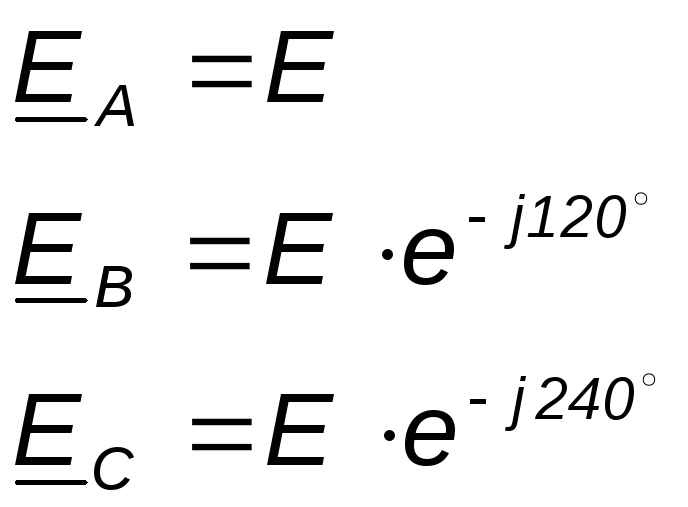
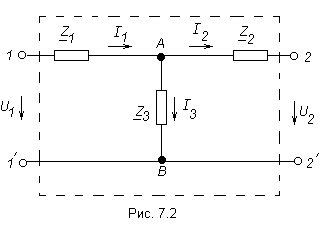 - и П – образные схемы замещения
представлены на (рис. 7.2 и 7.3)
соответственно.
- и П – образные схемы замещения
представлены на (рис. 7.2 и 7.3)
соответственно.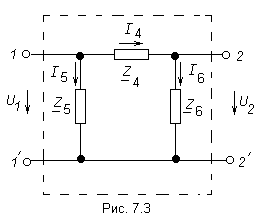 налогичные
приёмы для П- схемы дают:
налогичные
приёмы для П- схемы дают: