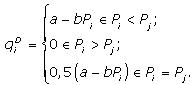Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.09.2024
Просмотров: 716
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 3. Теория потребительского спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
Глава 5. Ценообразование на монополизированном рынке
Глава 9. Отказы рынка и аллокативная роль государства
Глава 10. Микроэкономика внешней торговли
Глава 1. Введение в микроэкономику
1.1. Микроэкономика как часть современной экономической теории
1.2. Методы экономического анализа
1.3. Логическая структура курса
Глава 2. Теория производства и предложения благ
2.1. Производственная функция и техническая результативность производства
2.2. Затраты производства и функция затрат
2.3. Прибыль и условия ее максимизации
2.4. Функция предложения и излишек производителя
Глава 3. Теория потребительского спроса
3.3. Эффект замены и эффект дохода
3.4. Компенсационное и эквивалентное изменения дохода и излишки потребителя 7
3.5. Выявление предпочтений потребителя
3.6. Рыночный спрос и эластичность спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
4.1. Отраслевое равновесие и его разновидности
4.2. «Паутинообразная» модель ценообразования
4.3. Величина равновесной цены
4.4. Особенности рынка совершенной конкуренции
4.5. Последствия государственного регулирования цен
Глава 5. Ценообразование на монополизированном рынке
5.1. Цена, максимизирующая прибыль
5.3. Цены, максимизирующие выручку и норму прибыли
5.4. Отсутствие функции предложения
5.5. Последствия государственного регулирования
Глава 6. Ценообразование на рынках несовершенной конкуренции
6.1. Монополистическая конкуренция
6.2.1. Олигополия на рынке гомогенного блага
6.2.2. Олигополия на рынке гетерогенного блага
6.3. Олигополия в свете теории игр
Глава 7. Ценообразование факторов производства
7.1. Предложение факторов производства
7.2. Спрос на факторы производства
7.3. Прокатная цена фактора производства
7.4. Функциональное распределение результатов производства
7.5. Капитальная цена фактора производства
Глава 8. Общее экономическое равновесие и общественное благосостояние
8.1. Цены частичного и общего равновесия
8.2. Модель общего экономического равновесия Вальраса
8.3. Конкурентное равновесие и общественное благосостояние
8.4. Первая теорема общественного благосостояния
8.5. Вторая теорема общественного благосостояния
Глава 9. Отказы рынка и аллокативная роль государства
9.2. Интернализация внешних эффектов
9.3. Производство общественных благ
9.4. Асимметричность информации
Глава 10. Микроэкономика внешней торговли
10.1. Основы международного разделения труда
10.1.1. Исходная модель Рикардо
К![]() ак
это происходит, можно посмотреть,
используя:
ак
это происходит, можно посмотреть,
используя:![]() 6.3.
6.3.
Обобщение модели Курно. На основе предпосылок модели дуополии Курно можно построить модель ценообразования на рынке с любым числом конкурентов.
Для
упрощения примем, что у всех конкурентов
одинаковые экономические затраты:
TCi = lqi,
где i = I, ..., n.
Тогда прибыль i-й
фирмы:
![]() i = Pqi - lqi;
так как P = g - h
i = Pqi - lqi;
так как P = g - h![]() ,
то
,
то
![]() i = [g - h(qI + qII + ... + qn)]qi - lqi = gqi - hqiqI + hqiqII + ... hqi2 ... + hqiqn - lqi.
i = [g - h(qI + qII + ... + qn)]qi - lqi = gqi - hqiqI + hqiqII + ... hqi2 ... + hqiqn - lqi.
Прибыль достигает максимума при
|
|
|
. |
|
Поскольку g - hqI - hqII ... - hqn = P, то условие максимизации прибыли для отдельной фирмы имеет вид P = hqi + l.
Из него следует, что qi* = (P - l)/h, т.е. в состоянии равновесия все фирмы будут иметь одинаковый объем реализации. Это вытекает из допущения, что у всех фирм одинаковые предельные затраты на производство.
Подставим объем равновесного выпуска отдельной фирмы в функцию отраслевого спроса, тогда
|
|
|
. |
|
При n = 1 получаем монопольную цену (см. выражение (5.3)), а по мере увеличения n цена приближается к предельным затратам.
Равновесие в модели Курно характеризуется тем, что ни одному конкуренту не выгодно менять свое поведение, пока поведение других конкурентов остается неизменным. Такое состояние называют равновесием Нэша7.
![]()
Модель дуополии Штакельберга8
В отличие от модели Курно, в которой обе фирмы являются на рынке равноправными игроками, в модели Штакельберга одна из них (лидер I) активна, а другая (последователь II) пассивна. Последователь предоставляет лидеру возможность первому предложить на рынке желаемое количество товара и оставшийся после этого неудовлетворенный отраслевой спрос рассматривает как свою долю рынка.
Такое взаимоотношение между конкурентами может возникнуть вследствие ассиметричного распределения информации: лидер знает функцию затрат последователя, в то время как последователь не осведомлен о производственных возможностях лидера.
В такой ситуации фирмам не нужно принимать стратегических решений. Прибыль лидера зависит только от его объема выпуска, так как объем выпуска последователя задан уравнением его реакции: qII = qII(qI).
|
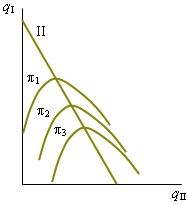
Для наглядного сопоставления равновесия Курно с равновесием Штакельберга линии реакции дуополистов нужно дополнить линиями равной прибыли (изопрофитами). Уравнение изопрофиты получается в результате решения уравнения прибыли дуополии относительно объема выпуска, обеспечивающего заданную величину прибыли. На рис. 6.4 показано, как располагаются изопрофиты фирмы II. При заданном выпуске фирмы I соответствующая ему точка на линии реакции фирмы II указывает объем ее производства, максимизирующий прибыль. Получить такую же прибыль при большем или меньшем своем выпуске фирма II может только, если фирма I уменьшит предложение на рынке, поэтому вершины изопрофит располагаются на линии реакции. Чем ниже расположена изопрофита, тем большую прибыль она представляет, так как соответствует меньшему выпуску конкурента. |
|
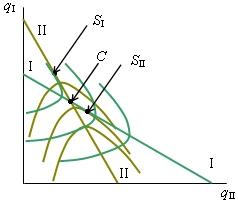
Совместив карты изопрофит дуополистов, можно увидеть сочетания qI,qII, соответствующие отраслевому равновесию в моделях Курно и Штакельберга (рис. 6.5). Точка пересечения линий реакции (С) представляет равновесие в модели Курно, а точка касания линии реакции последователя с наиболее низкой изопрофитой лидера представляет равновесие в модели Штакельберга (SI или SII). Из рис. 6.5 следует, что у фирмы, становящейся лидером, прибыль увеличивается по сравнению с той, которую она получала при конкуренции по модели Курно: лидер переходит на более низкую изопрофиту.
П |
Можно доказать, что при линейных функциях отраслевого спроса и общих затрат дуополистов в модели Штакельберга рыночная цена будет ниже, чем в модели Курно9.
Картель. Поскольку максимальную прибыль на рынке гомогенного блага обеспечивает монопольная цена, то наибольшую прибыль дуополисты (олигополисты) получат в случае организации картеля - явного или тайного сговора об ограничении рыночного предложения с целью поддержания монопольной цены.
Однако картельное соглашение не является равновесием Нэша, так как каждый участник картеля может повысить прибыль за счет увеличения своего выпуска, пока другие придерживаются соглашения. Вероятность нарушения картельного соглашения возрастает по мере увеличения числа его членов.
С![]() равнительный
анализ трех рассмотренных вариантов
функционирования рынка олигополии
представляют:
равнительный
анализ трех рассмотренных вариантов
функционирования рынка олигополии
представляют:
![]() и
и
![]() 6.5.
6.5.
Ценовая конкуренция
Модель Бертрана. Ж. Бертран, профессор политехнической школы в Париже, в 1883 г. опубликовал статью, в которой критиковал модель дуополии Курно за то, что в ней конкуренты определяют объем выпуска, а не цену товара. Это, по мнению Бертрана, не соответствует практике: олигополисты предлагают покупателям каталоги своей продукции, в которых указаны цены, а не предполагаемые объемы продаж. В модели дуополии Бертрана конкуренты принимают решения не об объеме выпуска, а о ценах.
Рассмотрим сначала поведение дуополистов, имеющих постоянные предельные затраты: (MC = l). Отраслевой спрос задан функцией QD = a - bP. Поскольку обе фирмы производят гомогенное благо, то функция спроса на продукцию одной фирмы имеет вид
|
|
|
|
|
Фирме достается весь рынок, если цена на ее продукцию ниже цены продукции конкурента; при обратном соотношении цен фирма вытесняется с рынка. Последний делится поровну между конкурентами, если они продают товар по одинаковой цене.
В таких условиях равновесие на рынке установится только в том случае, когда обе фирмы продают товар по одинаковой цене, которая равна предельным затратам: PI = PII = l, так как при PI = PII > l у каждого конкурента есть возможность захватить весь рынок за счет выбора цены в интервале l < P<SUB&NBSP;>i < P<SUB&NBSP;>j. В результате при ограниченном числе конкурентов на рынке устанавливается такая же цена, как на рынке совершенной конкуренции.
Когда дуополисты имеют возрастающие предельные затраты, последствия ценовой конкуренции многовариантны. Для конкретизации анализа используем следующие числовые функции затрат и отраслевого спроса:
|
|
|
|
|
Проверим, установится ли на рынке равновесие при P = MC:
16 - 2q = 1 + q ![]() q = 5; P = 6.
q = 5; P = 6.
Поделив
пополам рынок, каждая фирма получает
прибыль
![]() i = 6·5 - 5 - 12,5 = 12,5.
i = 6·5 - 5 - 12,5 = 12,5.
Что будет, если, например, фирма I решит повысить цену до 7, а фирма II не последует за ней? В отличие от ситуации с постоянными предельными затратами фирма I не окажется за пределами рынка, так как при P = 7 одна фирма не может предложить больше 6 единиц продукции из-за того, что предельные затраты превысят цену.
Поэтому при возрастающих предельных затратах состояние, в котором дуополисты поделили рынок пополам при цене, равной предельным затратам, не является устойчивым.
Определим,
на какую прибыль может рассчитывать
фирма I при PI = 7
и PII = 6.
Так как фирма II продает 5 ед. товара,
то спрос на продукцию фирмы I предстает
в виде: qI + 5 = 16 - PI ![]() qI = 11 - PI.
Следовательно, по цене PI = 7
фирма I продаст 4 ед. и получит
прибыль
qI = 11 - PI.
Следовательно, по цене PI = 7
фирма I продаст 4 ед. и получит
прибыль
![]() I =
7·4 - 4 - 8 = 16.
I =
7·4 - 4 - 8 = 16.
Таким образом, при растущих предельных затратах в модели Бертрана не существует равновесия Нэша и предсказать цену невозможно.
Ценообразование за лидером. В модели Бертрана конкуренты выступают на рынке в качестве равноправных игроков. Но бывают случаи, когда одна из фирм (лидер) имеет существенные преимущества перед другой (другими) по производственным мощностям и затратам на производства. В таких условиях цену на рынке устанавливает лидер, а другой продавец (аутсайдер) вынужден принять цену в качестве экзогенного параметра. Аутсайдер оказывается в положении конкурентной фирмы на рынке совершенной конкуренции и увеличивает свое предложение до тех пор пока предельные затраты не сравняются с ценой, установленной лидером.
|
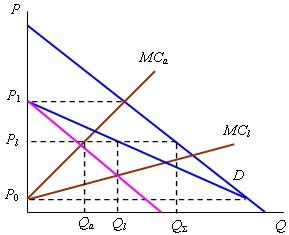
Рассмотрим
рис. 6.7. На нем линия D
представляет отраслевой спрос, линии
MCa
и MCл
- соответственно предельные затраты
аутсайдера и лидера. Когда цена
поднимается до P1,
тогда аутсайдер один может удовлетворить
отраслевой спрос. При цене P0
аутсайдер уходит с рынка. Если цена
устанавливается в интервале {P1, P0},
то рынок в определенной пропорции
делится между обоими конкурентами.
В результате вычитания функции
предложения аутсайдера из функции
отраслевого спроса (горизонтального
вычитания линии MCa
из линии D)
образуется функция спроса на продукцию
лидера - (Dl)
Пересечение соответствующей ей линии
MRл
с линией MCl
указывает на выпуск (Qл)
и цену (Pл)
лидера, максимизирующие его прибыль.
По этой цене аутсайдер предложит
объем продукции Qa
поскольку по построению Qл + Qa = Q |
![]()
![]() и
и
![]() 6.6
помогут Вам в этом разобраться.
6.6
помогут Вам в этом разобраться.