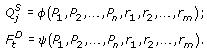Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.09.2024
Просмотров: 704
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 3. Теория потребительского спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
Глава 5. Ценообразование на монополизированном рынке
Глава 9. Отказы рынка и аллокативная роль государства
Глава 10. Микроэкономика внешней торговли
Глава 1. Введение в микроэкономику
1.1. Микроэкономика как часть современной экономической теории
1.2. Методы экономического анализа
1.3. Логическая структура курса
Глава 2. Теория производства и предложения благ
2.1. Производственная функция и техническая результативность производства
2.2. Затраты производства и функция затрат
2.3. Прибыль и условия ее максимизации
2.4. Функция предложения и излишек производителя
Глава 3. Теория потребительского спроса
3.3. Эффект замены и эффект дохода
3.4. Компенсационное и эквивалентное изменения дохода и излишки потребителя 7
3.5. Выявление предпочтений потребителя
3.6. Рыночный спрос и эластичность спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
4.1. Отраслевое равновесие и его разновидности
4.2. «Паутинообразная» модель ценообразования
4.3. Величина равновесной цены
4.4. Особенности рынка совершенной конкуренции
4.5. Последствия государственного регулирования цен
Глава 5. Ценообразование на монополизированном рынке
5.1. Цена, максимизирующая прибыль
5.3. Цены, максимизирующие выручку и норму прибыли
5.4. Отсутствие функции предложения
5.5. Последствия государственного регулирования
Глава 6. Ценообразование на рынках несовершенной конкуренции
6.1. Монополистическая конкуренция
6.2.1. Олигополия на рынке гомогенного блага
6.2.2. Олигополия на рынке гетерогенного блага
6.3. Олигополия в свете теории игр
Глава 7. Ценообразование факторов производства
7.1. Предложение факторов производства
7.2. Спрос на факторы производства
7.3. Прокатная цена фактора производства
7.4. Функциональное распределение результатов производства
7.5. Капитальная цена фактора производства
Глава 8. Общее экономическое равновесие и общественное благосостояние
8.1. Цены частичного и общего равновесия
8.2. Модель общего экономического равновесия Вальраса
8.3. Конкурентное равновесие и общественное благосостояние
8.4. Первая теорема общественного благосостояния
8.5. Вторая теорема общественного благосостояния
Глава 9. Отказы рынка и аллокативная роль государства
9.2. Интернализация внешних эффектов
9.3. Производство общественных благ
9.4. Асимметричность информации
Глава 10. Микроэкономика внешней торговли
10.1. Основы международного разделения труда
10.1.1. Исходная модель Рикардо
|
|
|
|
|
На основе выведенных функций строится микроэкономическая модель общего экономического равновесия, состоящая из трех групп уравнений, представляющих:
1) условия равновесия на рынках благ
|
|
|
; |
(8.8) |
j = 1,2,..., n;
2) условия равновесия на рынках факторов производства
|
|
|
|
(8.9) |
t = 1,2,..., m;
3) бюджетные ограничения фирм в условиях совершенной конкуренции в виде равенства общей выручки общим затратам
|
|
|
|
(8.10) |
j = 1,2,..., n;
Система уравнений (8.8) - (8.10) содержит (2n + m) неизвестных (Pj, rt, Qi) и столько же уравнений. Но независимыми являются только (2n + m - 1) уравнений. Это вытекает из бюджетного ограничения каждого потребителя.
Так, если в экономике используются два фактора производства (L, K) и производятся два блага (А, В), то для каждого экономического субъекта выполняется равенство
|
|
|
. |
(8.11) |
Равенство (8.11) означает, что расходы субъекта на покупку благ и факторов производства (левая часть) равны его доходам от продажи благ и предоставления услуг труда и капитала (правая часть). Представим его в другом виде
|
|
|
. |
|
В скобках представлен результат сделок экономического субъекта на каждом из рынков. Из-за бюджетного ограничения суммарный результат равен нулю.
Сложив результаты сделок всех участников на всех рынках, получим следующее равенство:
|
|
|
. |
(8.12) |
Каждое из слагаемых правой части равенства (8.12) характеризует конъюнктуру на отдельном рынке. Если оно равно нулю, то на рынке достигнуто равновесие; в противном случае на рынке существует дефицит или избыток. Из равенства (8.12) вытекают два важных свойства национальной экономики.
Во-первых, при отсутствии общего экономического равновесия сумма избытков на одних рынках равна сумме дефицитов на других.
Во-вторых, если некоторая система цен обеспечивает равновесие на любых трех рынках (превращает в нуль разность в любых трех скобках равенства (8.12)), то равновесие будет и на четвертом рынке (нулю будет равна и разность в четвертой скобке). Этот вывод, верный для любого числа рынков, назван законом Вальраса.
В соответствии с законом Вальраса система уравнений (8.8) - (8.10) содержит только (2n + m - 1) независимых уравнений. Чтобы она могла иметь решение, необходимо либо добавить еще одно независимое уравнение, либо исключить одно неизвестное. Первый вариант используется в макроэкономике; в качестве дополнительного берется уравнение, определяющее равенство спроса и предложения на денежном рынке. Второй вариант применяется в микроэкономике. Для объяснения микроэкономических явлений достаточно знать систему относительных цен, которая основана на том, что определенное количество одного товара служит масштабом цен при измерении ценности всех других товаров. Цена избранного товара принимается за единицу и в системе уравнений (8.8) - (8.10) число неизвестных оказывается равным числу независимых уравнений.
Как известно из математики, само по себе такое равенство не гарантирует существования решения соответствующей системы уравнений, особенно если искомые переменные должны иметь положительные значения. В этом мы могли убедиться в 8.1. Тем не менее доказано2, что при наложении ряда экономически приемлемых ограничений на характер функций и значения аргументов модели типа (8.8) - (8.10), можно определить вектор равновесных цен. Доказательство этого утверждения требует использования сложных математических выкладок.
В![]() ы
можете убедиться в возможности
существования общего экономического
равновесия, рассмотрев числовой
ы
можете убедиться в возможности
существования общего экономического
равновесия, рассмотрев числовой![]() 8.1
и выполнив
8.1
и выполнив
![]() с
диалоговыми упражнениями.
с
диалоговыми упражнениями.
Пример
|
Условие: Экономика состоит из двух потребителей (I,II) и двух фирм (A, B), производящих по одному виду продукции. Предпочтения потребителей представлены их функциями полезности:
где Qj,i количество j-го блага, потребляемого i-м индивидом.
В
Доходы
(бюджеты) потребителей формируются
за счет продажи фирмам труда и капитала:
Кроме того, при наличии у фирм прибыли она полностью распределяется между собственниками капитала, т.е. потребитель I получает 60%, а потребитель II – 40% прибыли. Фирмы работают по технологиям, представленным следующими производственными функциями:
В Цель потребителей – максимизация функций полезности, цель фирм – максимизация прибыли. Для каждого экономического субъекта цены на блага и факторы производства экзогенно заданы. Определим для данной экономики систему равновесных цен. |
Формализуем сперва поведение фирм:
Из
условия равновесия фирмы
![]() следует:
следует:![]() .
Поэтому
общие затраты фирмыА
равны:
.
Поэтому
общие затраты фирмыА
равны:
![]() ,
а
прибыль:
,
а
прибыль: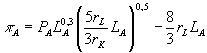 .
Она
достигает максимума при
.
Она
достигает максимума при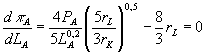 .
.
Отсюда определяются функции спроса фирмы А на труд и капитал в состоянии равновесия:
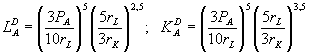 .
.
Подставив эти значения в производственную функцию, получим функцию предложения фирмы А:
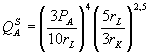 .
.
В![]() графическом виде выведенные функции
можно представить, задав значения цен
на факторы производства:
графическом виде выведенные функции
можно представить, задав значения цен
на факторы производства:![]() 3.
3.
Аналогично определяются функции спроса на факторы производства и предложения блага для фирмы В:
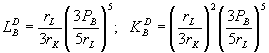 ;
;
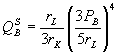 .
.
Обратим
внимание на то, что объемы спроса и
предложения производителей определяются
только системой цен. Поэтому и прибыль
можно представить в виде функции от
вектора цен. Используя формулу
![]() ,
получаем:
,
получаем:
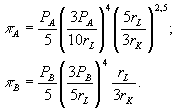
Для определения бюджета потребителей нам потребуется величина суммарной прибыли обеих фирм:
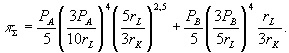
Теперь перейдем к формализации поведения потребителей
Потребители I и II максимизируют свои функции полезности при следующих бюджетных ограничениях:
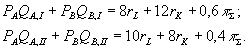
На
основе функции полезности потребителя I
и его бюджетного уравнения составим
функцию Лагранжа:
![]() .
Из
условий ее максимизации
.
Из
условий ее максимизации![]() следует
следует![]() .
.
Подставив полученное значение в бюджетное уравнение, определим функции спроса потребителя I на каждое благо:
![]()
Аналогично выводятся функции спроса на блага потребителя II:
![]()
На основе выведенных функций составим модель общего экономического равновесия:
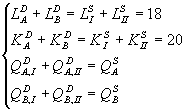
В
соответствии с законом Вальраса вектор
цен, обеспечивающий равновесие на трех
первых рынках, уравнивает спрос и
предложение и на четвертом рынке. На
основе выведенных выше функций
![]() получаем
систему:
получаем
систему:
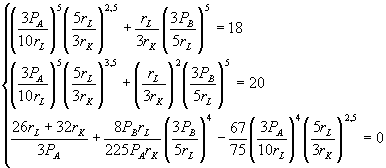
Чтобы
довести число неизвестных до числа
уравнений, примем:
![]() .
Тогда из решения системы получаем:
.
Тогда из решения системы получаем:![]() При
таких ценах
При
таких ценах![]() Тогда
бюджет первого потребителя–
MI =
Тогда
бюджет первого потребителя–
MI = ![]() ,
а бюджет второго –
MII =
,
а бюджет второго –
MII = ![]() .
.
Эта система цен обеспечивает совместное равновесие на всех четырех рынках:
|
|
Потребитель |
Фирма |
||||
|
Рынок |
I |
II |
всего |
А |
В |
всего |
|
|
предложение |
спрос |
||||
|
Труда |
8 |
10 |
18 |
6,16 |
11,84 |
18 |
|
Капитала |
12 |
8 |
20 |
14,45 |
5,55 |
20 |
|
|
спрос |
предложение |
||||
|
Блага А |
4,55 |
2,01 |
6,56 |
6,56 |
|
6,56 |
|
Блага В |
2,24 |
3,97 |
6,21 |
|
6,21 |
6,21 |