Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc

Для количественной характеристики технической результативности производства в коротком периоде применяют три взаимосвязанных показателя: среднюю производительность, предельную производительность и эластичность выпуска по переменному фактору.

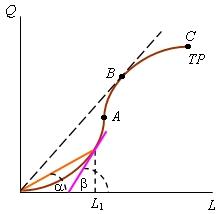
Отношение общего объема выпуска к общему количеству используемого переменного фактора (Q/L) называют средней производительностью переменного фактора АР (average product). Графически она представляется наклоном прямой, соединяющей точки кривой ТР с началом координат. На рис. 2.2 средняя производительность труда при его использовании в объеме L₁ единиц равна tg. Средняя производительность труда по мере увеличения его количества при данном объеме капитала сначала повышается (на рис. 2.2 до точкиВ), а затем снижается.

Обратим внимание на две примечательные особенности:

1. Снижение средней производительности переменного фактора начинается тогда, когда значения предельной и средней производительностей становятся равными (в точке В на рис. 2.2 tg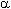= tg).

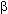2. После достижения определенной капиталовооруженности труда 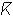/L_A его предельная производительность монотонно снижается, т.е. начинает действовать, так называемый, «закон снижающейся предельной производительности» переменного фактора производства.

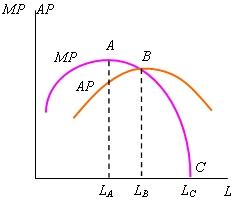
На основе изменения tgи tgпо мере увеличения количества используемого труда можно построить кривые его средней и предельной производительностей (рис. 2.3).

Из рис. 2.3 следует, что при увеличении количества используемого труда от 0 до L_B имеет место _Q,L > 1; при L = L_B коэффициент _Q,L = 1; в интервале L_B < L < L_C эластичность выпуска по переменному фактору убывает от 1 до 0, а при использовании заданного объема капитала и количестве труда больше L_C коэффициент эластичности принимает отрицательное значение.

Таким образом, техническая результативность производства в коротком периоде проходит четыре стадии (I-IV), представленные в табл. 2.1 (на рис. 2.2 и 2.3 они отделены друг от друга точками А, В и С).

Таблица 2.1

Стадии технической результативности производства в коротком периоде

Практический аспект проведенного анализа заключается в том, чтобы определить, какой объем переменного фактора целесообразно использовать в коротком периоде. Очевидно, что на стадии I надо увеличивать занятость, а переходить в стадию IV экономически нецелесообразно. Стоит ли переходить в стадии II и III? Для ответа на этот вопрос, кроме технологии, нужно знать цены производимой продукции и факторов производства. После того, как они будут введены в наш анализ, можно будет ответить на поставленный вопрос.

При использовании показателей средней и предельной производительностей, а также эластичности весь выпуск, как бы, вменяется только одному, переменному фактору. Но с не меньшим основанием результат производства можно «приписать» постоянному фактору. Его средняя производительность AP_K = Q/. Она повышается при увеличении количества применяемого труда до тех пор, пока растет общий выпуск. Но поскольку в коротком периоде решения принимают по поводу объемов использования переменного фактора, то определяют показатели его результативности.

Техническая результативность производства в длинном периоде

Так как в длинном периоде меняется не только количество используемого в производстве труда, но и объем капитала, то производственную функцию в нем можно представить в виде множества производственных функций в коротком периоде, различающихся объемами капитала. Шесть таких функций приведены в табл. 2.2. В столбцах показано изменение выпуска по мере увеличения труда при фиксированных объемах капитала, а в строках - при росте капитала и неизменных объемах труда. В целом это есть табличная форма представления производственной функции в длинном периоде.

Таблица 2.2

Табличная форма производственной функции длинного периода

Данные, приведенные в табл. 2.2, отражают «закон снижающейся предельной производительности и труда, и капитала». Это выражается в том, что значения величин в столбцах и строках растут медленнее, чем значения, отражающие увеличение соответственно количества применяемого труда и объема капитала. Эту особенность производственной функции в длинном периоде необходимо учитывать при выборе алгебраической формы ее представления. Для данной цели не подходит, например, функция вида Q = aL + bK, где а и b - константы, так как в этом случае предельные производительности факторов производства неизменны.

Типичной формой производственной функции в длинном периоде является степенная функция вида:

,

где А, ,- положительные постоянные числа, характеризующие технологию производства.

Широкое применение в экономическом анализе получила функция Кобба - Дугласа²

Табл. 2.2 представляет именно такую функцию. В ней данные округленные до целых чисел соответствуют формуле Q = L^0,75K^0,25.

Показатели степеней ипроизводственной функции равны коэффициентам эластичности выпуска по факторам

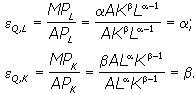
При попытке оценить результативность производства в длинном периоде путем деления общего выпуска продукции на количество используемых факторов возникает затруднение из-за того, что нельзя суммировать число рабочих с числом станков или гектарами земли. Тем не менее определенную характеристику технологии можно получить, наблюдая за изменением выпуска при изменении объемов обоих факторов производства в одно и то же число раз, т.е. меняя масштаб производства. Результат воздействия на выпуск пропорционального изменения обоих факторов называют эффектом масштаба (returns to scale)³.

Рост объемов труда и капитала в n раз может сопровождаться увеличением выпуска: 1) в n раз; 2) более, чем в n раз; 3) менее, чем в n раз. В первом случае говорят, что технология имеет неизменный эффект масштаба, во втором - растущий и в третьем - снижающийся. В табл. 2.3 приведены числовые примеры для каждого из них.