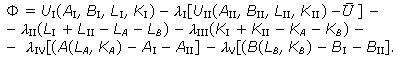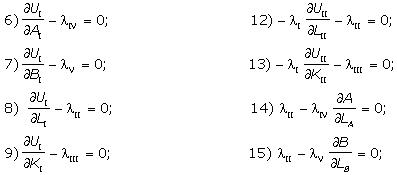Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc

Допустим, что это не так и индивид I завидует индивиду II, т.е. предпочитает набор набору. Это значит, что должно иметь место следующее неравенство:

<,

т.е. бюджет индивида I меньше бюджета индивида II.

Но при добровольном обмене по единым для всех участников сделки ценам этого быть не может, так как обмен происходил при соблюдении бюджетных ограничений каждого из субъектов

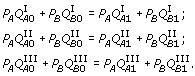
Поскольку правые части всех трех уравнений равны друг другу из-за первоначального уравнительного распределения, то и левые части должны быть равны друг другу. Следовательно, конкурентное равновесие, установившееся после обмена по равновесным ценам на основе первоначального уравнительного распределения, достигнуто при справедливом и Парето-эффективном распределении.

Краткие выводы

Вследствие взаимозависимости цен всех благ и факторов производства полное представление о механизме рыночного ценообразования и его роли в национальной экономике можно получить лишь на основе построения модели общего экономического равновесия, отображающей взаимодействие всех рынков. Из этой модели выводится система равновесных цен, обеспечивающая совместное равновесие на всех рынках, и определяются условия ее существования.

Чтобы установить, является ли общее экономическое равновесие наилучшим для общества состоянием экономики, необходим критерий общественного благосостояния. Трудности, возникающие при построении такого критерия, проистекают из того, что он должен отражать не только уровень благосостояния образующих общество индивидов, но и предпочтения общества относительно степени дифференциации его членов по уровню благосостояния. Решение проблемы осложняется, в частности, тем, что общественные предпочтения, отражающие мнение большинства, не транзитивны. Нейтральным к распределению национального дохода между индивидами является критерий Парето-эффективности.

В соответствии с ним экономическая эффективность общественного хозяйства растет лишь в тех случаях, когда повышение благосостояния одних не сопровождается снижением благосостояния других членов общества. При таком подходе проблема экономической эффективности отделяется от проблемы распределения благосостояния между индивидами.

Общее экономическое равновесие, достигнутое в условиях существования совершенной конкуренции на всех рынках, является Парето-эффективным состоянием.

Парето-эффективное состояние экономики может быть достигнуто при различных уровнях дифференциации благосостояния индивидов.

Если предпочтения потребителей и технологии производства благ выпуклы, то любому Парето-эффективному состоянию экономики можно подобрать вектор равновесных цен, поддерживающих такое состояние в условиях совершенной конкуренции. Поэтому в названных условиях проблема эффективного использования факторов производства может решаться отдельно от проблемы распределения благосостояния между членами общества. Система равновесных цен может направлять производство и обмен на Парето-эффективное использование ресурсов общества, а посредством перераспределительной политики государства можно поддерживать распределение благосостояния между гражданами в соответствии с представлениями общества о социальной справедливости. Но при этом государство должно применять такие инструменты перераспределения, которые не деформируют систему равновесных цен.

ТЕСТ

Математическое приложение 1: Выведение функций индивидуального спроса на блага и предложения труда

Максимум функции

достигается при условиях

Разделив первое условие на второе, получим

Разделив условие «1» на условие «3», получим

Подставим значения (1) и (2) в бюджетное уравнение

и решим его относительно Q_A

Подставив значение (3) в равенства (1) и (2), после преобразований получим

Математическое приложение 2. Определение условий совместной оптимальности по Парето в производстве и обмене

В хозяйстве имеются два потребителя (I и II), каждый из которых имеет определенное количество труда и капитала (L_I, K_I и L_II, K_II). Факторы производства используются для выпуска двух разновидностей благ (А и В) по технологиям, представленным производственными функциями:

A = A(L_A, K_A); B = B(L_B, K_B),

где L_A, K_A, L_B, K_B количества соответственно труда и капитала, использующиеся для выпуска каждого из благ.

Предпочтения потребителей, определяющие их спрос на блага, и предложение принадлежащих им факторов заданы функциями полезности

U_I = U_I(A_I, B_I, L_I, K_I); U_II = U_II(A_II, B_II, L_II, K_II).

В приведенных условиях оптимальное по Парето состояние в обмене и производстве одновременно устанавливается тогда, когда функция полезности одного из потребителей (возьмем I) достигает максимума при заданном благосостоянии (заданном значении функции полезности) другого:

U_I(A_I, B_I, L_I, K_I)  max

при следующих ограничениях:

1) U_II(A_II, B_II, L_II, K_II) =  = const; 2) L_I + L_II = L_A + L_B; 3) K_I + K_II = K_A + K_B; 4) A_I + A_II = A(L_A, K_A); 5) B_I + B_II = B(L_B, K_B).

Соответствующая данной задаче функция Лагранжа имеет вид

Условием ее максимизации является следующая система уравнений:

Из решения системы уравнений «1» - «17» наряду со значениями пяти сомножителей Лагранжа определяются значения 12 натуральных показателей, представляющих Парето-эффективное состояние одновременно в обмене и производстве:

Чтобы условия достижения Парето-эффективности одновременно в обмене и производстве представить в виде равенства (8.13), разделим условие «6» на условие «7»

условие «10» на условие «11»

условие «14» на условие «15»

условие «16» на условие «17»

Из равенств (а) - (г) следует, что

т.е. .