Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.09.2024
Просмотров: 731
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 3. Теория потребительского спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
Глава 5. Ценообразование на монополизированном рынке
Глава 9. Отказы рынка и аллокативная роль государства
Глава 10. Микроэкономика внешней торговли
Глава 1. Введение в микроэкономику
1.1. Микроэкономика как часть современной экономической теории
1.2. Методы экономического анализа
1.3. Логическая структура курса
Глава 2. Теория производства и предложения благ
2.1. Производственная функция и техническая результативность производства
2.2. Затраты производства и функция затрат
2.3. Прибыль и условия ее максимизации
2.4. Функция предложения и излишек производителя
Глава 3. Теория потребительского спроса
3.3. Эффект замены и эффект дохода
3.4. Компенсационное и эквивалентное изменения дохода и излишки потребителя 7
3.5. Выявление предпочтений потребителя
3.6. Рыночный спрос и эластичность спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
4.1. Отраслевое равновесие и его разновидности
4.2. «Паутинообразная» модель ценообразования
4.3. Величина равновесной цены
4.4. Особенности рынка совершенной конкуренции
4.5. Последствия государственного регулирования цен
Глава 5. Ценообразование на монополизированном рынке
5.1. Цена, максимизирующая прибыль
5.3. Цены, максимизирующие выручку и норму прибыли
5.4. Отсутствие функции предложения
5.5. Последствия государственного регулирования
Глава 6. Ценообразование на рынках несовершенной конкуренции
6.1. Монополистическая конкуренция
6.2.1. Олигополия на рынке гомогенного блага
6.2.2. Олигополия на рынке гетерогенного блага
6.3. Олигополия в свете теории игр
Глава 7. Ценообразование факторов производства
7.1. Предложение факторов производства
7.2. Спрос на факторы производства
7.3. Прокатная цена фактора производства
7.4. Функциональное распределение результатов производства
7.5. Капитальная цена фактора производства
Глава 8. Общее экономическое равновесие и общественное благосостояние
8.1. Цены частичного и общего равновесия
8.2. Модель общего экономического равновесия Вальраса
8.3. Конкурентное равновесие и общественное благосостояние
8.4. Первая теорема общественного благосостояния
8.5. Вторая теорема общественного благосостояния
Глава 9. Отказы рынка и аллокативная роль государства
9.2. Интернализация внешних эффектов
9.3. Производство общественных благ
9.4. Асимметричность информации
Глава 10. Микроэкономика внешней торговли
10.1. Основы международного разделения труда
10.1.1. Исходная модель Рикардо
Прибыль водоснабжающей станции равна:
![]() B = PBQB - CB(QB,h).
B = PBQB - CB(QB,h).
Условие ее максимизации:
|
|
|
. |
(9.2) |
Из равенств (9.1) и (9.2) определяются объемы производства красителей, загрязнений и годной к потреблению волы.
Чтобы выяснить, является ли такое использование ресурсов наилучшим для всего хозяйства, изменим организационную форму его ведения. Предположим, что химический завод и станция водоснабжения объединились в одну фирму, деятельность которой будет направлена на максимизацию суммарной прибыли от продажи красителей и воды. Прибыль в этом случае определяется по формуле:
|
|
|
. |
|
Условием её максимизации является система уравнений:
|
|
|
|
(9.3) |
Прибыль
объединенной фирмы достигает максимума,
когда прирост прибыли от очередной
порции загрязнений становится равным
предельному приросту затрат водоснабжающей
станции от этого загрязнения. Так как
![]() то
объединенная фирма прекратит выпуск
красителей до достижения равенства
то
объединенная фирма прекратит выпуск
красителей до достижения равенства![]() т.е.
для хозяйства в целом целесообразно
снизить объем загрязнения, хотя и не до
нуля.
т.е.
для хозяйства в целом целесообразно
снизить объем загрязнения, хотя и не до
нуля.
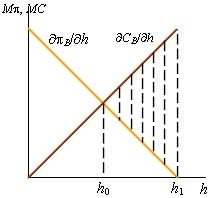
Графическое сравнение аллокаций, возникающих в обоих рассмотренных случаях, представлено на рис. 9.3. При производстве обоих благ в самостоятельных фирмах в реку будет спущено h1 загрязнений; объединенная фирма произведет лишь h0 загрязнений. Чистый выигрыш общества от снижения производства красителей показан заштрихованной областью.
|
За возникновением положительного внешнего эффекта проследим на числовом примере.
В
городе функционируют две фирмы сферы
услуг - спортивный комплекс и
поликлиника. Функция затрат эксплуатации
спортивного комплекса имеет вид:
|
Чтобы
проверить, нельзя ли повысить эффективность
использования ресурсов, занятых в двух
рассматриваемых фирмах, объединим
спорткомплекс и поликлинику в одну
фирму. Ее прибыль
![]() =PCQC + PnQn - 0,25Q2C - 2Q2n + QC - 5
будет максимальной, если PC + 1 = 0,5QC
и Pn = 4Qn;
следовательно функции предложения
объединенной фирмы имеют вид: QSC = 2PC + 2
и QSn = 0,25Pn,
т.е. при том же предложении медицинских
услуг объединенное предприятие
увеличивает объем спортивно-оздоровительных
мероприятий.
=PCQC + PnQn - 0,25Q2C - 2Q2n + QC - 5
будет максимальной, если PC + 1 = 0,5QC
и Pn = 4Qn;
следовательно функции предложения
объединенной фирмы имеют вид: QSC = 2PC + 2
и QSn = 0,25Pn,
т.е. при том же предложении медицинских
услуг объединенное предприятие
увеличивает объем спортивно-оздоровительных
мероприятий.
Рассмотренные примеры показывают, что при наличии внешних эффектов рыночный механизм не обеспечивает оптимальной по Парето аллокации. В этих случаях государство может способствовать более эффективному использованию ресурсов либо через систему налогообложения и дотаций, либо путем закрепления собственности на право производить внешние эффекты. Идея использовать налог для достижения оптимальной по Парето аллокации принадлежит А. Пигу1 и основывается на том, что при наличии отрицательных внешних эффектов частные затраты производства блага меньше общественных затрат его производства. Введение налога должно уравнять эти два вида затрат.
Определим
величину налога Пигу, необходимого для
эффективного производства красителей
в рассмотренном выше примере. Если
химический завод за каждую единицу
загрязнений должен уплачивать налог в
размере
![]() ден.
ед., то его прибыль будет определяться
по формуле:
ден.
ед., то его прибыль будет определяться
по формуле:
|
|
|
|
|
Она достигает максимума при условии:
|
|
|
. |
(9.4) |
Из
сопоставления условия (9.4) с условием (9.3),
определяющим оптимальной по Парето
объем производства красителей, следует,
что при
![]() химический
завод максимизирует прибыль при
оптимальной по Парето объеме производства,
т.е. ставка налога Пигу должна равняться
предельному приращению затрат на очистку
воды при оптимальной по Парето аллокации.
химический
завод максимизирует прибыль при
оптимальной по Парето объеме производства,
т.е. ставка налога Пигу должна равняться
предельному приращению затрат на очистку
воды при оптимальной по Парето аллокации.
|
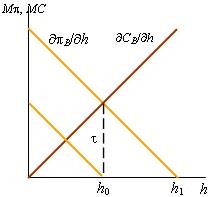
Как меняется ситуация, изображенная на рис. 9.3, при введении налога Пигу, показано на рис. 9.4. График предельной чистой прибыли завода смещается вниз на величину ставки налога и оптимальный для завода объем загрязнения совпадает оптимумом для общества. Лауреат Нобелевской премии по экономике за 1991 г. Р. Коуз подверг критике идею интернализации внешних эффектов посредством налогов и предложил решать эту задачу закреплением собственности на право производить внешние эффекты, создавая тем самым рынок таких прав; тогда рынок обеспечит оптимальный по Парето объем внешнего эффекта2. Посмотрим, как это предложение может быть реализовано в примере с химическим заводом и станцией водоснабжения. |
Если химический завод имеет право произвести h1 ед. загрязнений, то станция водоснабжения может предложить заводу платить Ph ден. ед. за каждую не произведенную единицу загрязнений (конкретная величина Ph будет определена ниже). В этом случае прибыль химического завода будет определяться по формуле
|
|
|
|
|
Условием ее максимизации является система из двух уравнений:
|
|
|
. |
(9.5) |
Выручка станции водоснабжения уменьшится на сумму платежа заводу. Поэтому ее прибыль определяется по формуле:
|
|
|
|
|
Она достигает максимума при
|
|
|
. |
(9.6) |
Условия (9.5)-(9.6), из которых в данном случае определиться аллокация, полностью совпадают с условиями (9.3), определяющими оптимальную по Парето аллокацию. Из условий (9.5)-(9.6) видно, что цена загрязнений равна налогу Пигу:
|
|
|
. |
|
Допустим теперь, что право производить (разрешать) загрязнение водоема принадлежит станции водоснабжения. Тогда завод может предложить станции Ph ден. ед. за каждую единицу загрязнений. Прибыль станции будет равна
|
|
|
|
|
а прибыль завода:
|
|
|
|
|
Легко заметить, что и в этом случае условия максимизации прибыли будут описываться равенствами (9.5)-(9.6).
Таким образом, независимо от того, за кем закреплено право собственности на производство внешних эффектов рынок установит их оптимальный по Парето объем. Этот вывод получил название теоремы Коуза.
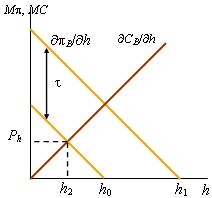
Повторим
логику рассуждений Р. Коуза, используя
рис. 9.3. Если завод имеет право на
загрязнения, то станции водоснабжения
выгодно заплатить за каждую единицу
уменьшения загрязнения с объема h1
до h0
по Ph ден. ед.
(напомним, что Ph соответствует
точке пересечения графиков предельной
прибыли завода и предельных затрат
станции), так как в этом интервале
![]() .
Заводу такое предложение тоже выгодно,
так как в интервале {h1, h0}
его предельная прибыль меньше Ph.
Когда станции водоснабжения принадлежит
право определять объем загрязнения,
тогда химический завод предложит ей
Ph ден. ед.
за каждую единицу загрязнения вплоть
до h0,
поскольку до такого объема загрязнений
его предельная прибыль превышает Ph.
Станция на это согласится, так как до
h0 ее
предельные затраты на очистку воды
меньше Ph.
.
Заводу такое предложение тоже выгодно,
так как в интервале {h1, h0}
его предельная прибыль меньше Ph.
Когда станции водоснабжения принадлежит
право определять объем загрязнения,
тогда химический завод предложит ей
Ph ден. ед.
за каждую единицу загрязнения вплоть
до h0,
поскольку до такого объема загрязнений
его предельная прибыль превышает Ph.
Станция на это согласится, так как до
h0 ее
предельные затраты на очистку воды
меньше Ph.
|
Аналогичные рассуждения лежат в основе критики Р. Коузом налога Пигу. Воспроизведем ситуацию, возникшую в рассматриваемом примере после введения налога Пигу, на рис. 9.5. Р. Коуз обращает внимание на то, что сложившаяся аллокация (производство h0 ед. загрязнений) неустойчива. Если станция водоснабжения предложит заводу сократить загрязнения на h0 - h2 ед., обещая за это заплатить Ph(h0 - h2) ден. ед., то в интересах завода принять это предложение. В результате обе фирмы улучшат свое положение, но аллокация перестанет быть Парео-оптимальной из-за введения налога Пигу. В заключение отметим, что внешние эффекты, могут интернализироваться и без участия государства. Поскольку при объединении фирм увеличивается совокупная прибыль за счет оптимизации размеров внешних эффектов, то конкурентный рынок сам устраняет внешние эффекты через слияния и поглощения. Однако укрупнение фирм имеет предел в виде падения эффективности от масштаба. |