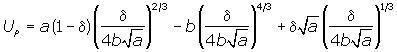Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc

В хозяйстве, состоящем из двух индивидов (I, II), производится один вид частного блага (A) и один вид общественного блага (Z). Известны индивидуальные функции полезности: U_I = U_I(Q_A_,I,Q_Z);U_II = U_II(Q_A_,II,Q_Z), где Q_A,i - количество частного блага, потребляемого i-м потребителем; Q_Z - количество общественного блага, одинаковое для каждого потребителя. Технология производства обоих благ представлена трансформационной функцией⁶: T(Q_A,Q_Z) = 0.

Производство общественного блага является оптимальным по Парето, если при заданном значении функции полезности II индивида функция полезности I достигает максимума, так как в этом случае нельзя повысить благосостояние одного из индивидов, не снижая благосостояние другого:

Функция Лагранжа в данном случае принимает вид:

Условия ее максимизации:

(1)

(2)

(3)

Разделим равенство (2) на равенство (1):

(4)

С учетом равенства (3) выражение (4) можно представить в виде:

что соответствует равенству .

Математическое приложение 2: Модель «принципал-агент»

При имеющемся у принципала капитале результаты хозяйственной деятельности являются стохастической функцией количества затрачиваемого агентом труда:

Q = aL + ,

где a - показатель производительности, - стохастическая переменная с нулевым ожиданием.

Денежный эквивалент своих физических и умственный затрат агент оценивает по формуле:

H = bL²; 0 < b < 1.

Оплата труда агента состоит из двух частей: фиксированной суммы, независящей от количества труда и выпуска (m) и доли () конечного результата хозяйственной деятельности:

M(r,,) =m + Q.

Агент согласен трудиться, если M H.

Вариант 1. Агент безразличен к риску и его усердие неконтролируемо.

В этом случае М = M(r,). Функция полезности агента имеет вид:

U_A = m + aL - bL²,

(1)

а принципала -

U_P = Q - M = aL - m - aL.

(2)

Отсюда функция общественного благосостояния:

W = U_A + U_P = aL - bL².

Она достигает максимума при a = 2bL L* = a/2b. Таков оптимальный объем использования труда.

Фактическое предложение труда определяется из условия максимизации функции (1):

(3)

Следовательно, чтобы L_S = L*, требуется = 1, т.е. весь результат хозяйственной деятельности нужно передать агенту.

Цель принципала - максимизировать функцию (2) при ограничении (3) и равенстве M = H:

m + aL = bL² m = bL² - aL.

(4)

Подставим значение (4) в функцию (2):

U_P = aL - bL² + aL - aL = aL - bL².

и заменим L его значением в выражении (3):

Функция полезности принципала достигает максимума при:

Таким образом и в интересах принципала передать весь результат агенту. В этом случае L^S = a/2b = L*. Подставив это значение в условие (4), найдем

Отрицательное значение фиксированной части оплаты труда агента означает, что с него надо брать арендную плату. Подставим значения арендной платы, L^S и = 1 в функцию полезности агента:

Таким образом, агент «остался при своих» и вся польза сотрудничества досталась принципалу.

Вариант 2. Агент склонен избегать риск и его усердие контролируемо.

Отобразим неприязнь агента к риску тем, что предельная полезность дохода от конечного результата для него убывает, т.е.

U_A = m + (aL)^0,5 - bL².

(5)

Функция полезности принципала остается прежней. Поэтому функция общественной полезности имеет вид:

W = [(aL)^0,5 - aL] + aL - bL².

Теперь общественное благосостояние зависит не только от количества затрачиваемого труда, но и от пропорции распределения экономического результата. Так как разность в квадратной скобке отрицательна, то общественное благосостояние достигает максимума при = 0, т.е. весь результат должен остаться у принципала. В этом случаеW = aL - bL² и оптимальный объем использования труда по-прежнему L* = a/2b, а найденная из выражения (4) автономная часть оплаты m = bL². Поскольку принципал может контролировать количество и качество труда, то система его оплаты такова:

Вариант 3. Агент склонен избегать риск и его усердие неконтролируемо.

Количество предлагаемого агентов труда определяется из условия максимизации его функции полезности (5):

(6)

Рис. 1. Функция полезности принципала

Теперь равенство М = Н, определяющее нижнюю границу оплаты труда агента, имеет вид:

(7)

Заменив в функции полезности принципала (2) L и r на их значения в выражениях (6) и (7), получим:

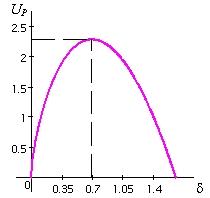
Примем а = 9; b = 0,25. В этом случае максимум полезности принципал получает при = 0,69 (см. рис. 1).

Смотрите также файлы

Савицкая - Лекции по микроэкономике - Глава 14.pdf

Савицкая - Лекции по микроэкономике - Глава 13.pdf

Савицкая - Лекции по микроэкономике - Глава 12.pdf

Савицкая - Лекции по микроэкономике - Глава 11.pdf

Савицкая - Лекции по микроэкономике - Глава 10.pdf

Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc

Смотрите также файлы

Информация

Списки файлов

Дополнительно