Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc

Технология производства	Объем выпуска при			Эффект масштаба
Технология производства	L = 20 К = 100	L = 30 К = 150	L = 40 К = 200	Эффект масштаба
Q = L^0,75K^0,25	29,9 (1)	44,9 (1,5)	59,8 (2)	Постоянный
Q = L^0,75K^0,5	94,6 (1)	157,0 (1,7)	224,9 (2,4)	Растущий
Q = L^0,5K^0,25	14,1 (1)	19,2 (1,4)	23,8 (1,7)	Снижающийся

Примечание. В скобках указано, во сколько раз увеличен выпуск по сравнению с исходным.

Поскольку показатели степеней в производственной функции Q = ALK показывают, на сколько процентов возрастет выпуск при увеличении соответствующего фактора производства на 1%, то при += 1 постоянный эффект масштаба; при+> 1 - растущий, а при+< 1 - снижающийся.

Рис.2.4. Карта изоквант

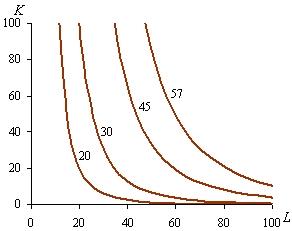
Для графического представления производственной функции в длинном периода в двухмерном пространстве используют семейство линий равного выпуска. Линия равного выпуска, или изокванта, представляет множество различных сочетаний объемов труда и капитала, при которых достигается один и тот же объем выпуска. Из табл. 2.2 следует, что 57 ед. продукции можно выпустить при трех различных комбинациях труда и капитала: K₁ = 50, L₁ = 60; K₂ = 30, L₂ = 70; K₃ = 20, L₃ = 80. Кроме этих трех комбинаций труда и капитала существует множество других, при которых по технологии, характеризующейся производственной функцией Q = L^0,75K^0,25, тоже можно произвести 57 ед. продукции. Соединив все точки, представляющие эти комбинации в системе координат K,L, получим изокванту 57. Аналогично строится изокванта для любого другого объема выпуска, в результате производственная функция в длинном периоде предстает в виде семейства или карты изоквант (рис. 2.4).

Это иллюстрирует: 2.2.

Изокванта является одним из основных инструментов графического анализа технической результативности производства. Поэтому выясним, чем определяются её конфигурация и расположение в пространстве K, L.

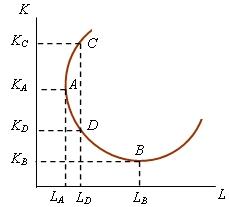
Рис. 2.5. Эффективная и неэффективная области изокванты

Поскольку производственная функция выражает зависимость между количеством используемых факторов и максимально возможным выпуском, то изокванта представляет множество сочетаний минимально необходимых объемов труда и капитала для заданного выпуска. Это означает, что изокванта не может иметь положительный наклон. Допустим, что она имеет вид, изображенный на рис. 2.5. В таком случае все точки, изокванты, расположенные вне дуги АВ, представляют неэффективные варианты производства 57 ед. продукции. Так, точка С соответствует варианту производства при использовании К_С единиц капитала и L_С единиц труда. Но 57 единиц продукции с такими же затратами труда можно произвести, применяя лишь K_D единиц капитала.

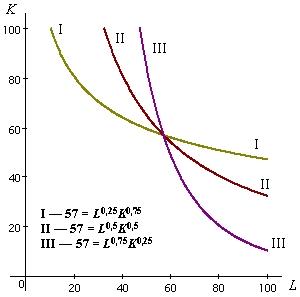
Расположение изокванты относительно осей координат определяется соотношением эластичностей выпуска по факторам производства (рис. 2.6). Если _Q,L = _Q,K, то изокванта симметрична биссектрисе, исходящей из начала координат. При _Q,L > _Q,K она имеет относительно больший наклон к оси, на которой откладывается объем труда, а при _Q,K > _Q,L, наоборот.

Рис. 2.6. Зависимость расположения изокванты от соотношения эластичностей выпуска по факторам производства

Проверьте это выполнив: 2.3.

Карта изоквант наглядно отображает эффект масштаба. Изокванты, соответствующие Q = Q₀, Q = 2Q₀, Q = 3Q₀, …, Q = nQ₀, при технологии с постоянным эффектом масштаба располагаются относительно друг друга на одинаковом расстоянии. При технологии с растущим эффектом от масштаба они приближаются друг к другу по мере увеличения выпуска, а с уменьшающим отодвигаются (рис. 2.7).

Изокванта свидетельствует о взаимозаменяемости факторов производства: заданный объем продукции можно эффективно произвести при различных сочетаниях труда и капитала (различной капиталовооруженности труда). В какой пропорции один из факторов можно заменить другим, зависит от исходной капиталовооруженности труда. Рассмотрим еще раз рис. 2.5. При переходе от сочетания К_A, L_А к сочетанию К_D, L_D на каждую дополнительную единицу труда высвобождается больше капитала, чем при переходе от сочетания К_D, L_D к сочетанию К_B, L_B. Это связано с тем, что дуга AD имеет более крутой наклон к оси абсцисс, чем дуга DB.

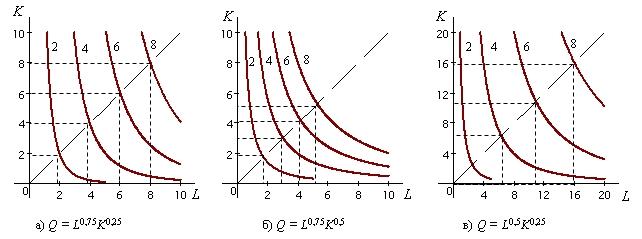Рис. 2.7. Карта изоквант при постоянном (а), растущем (б) и снижающемся (в) эффектах масштаба (цифры около кривых - количество выпускаемой продукции)

Это иллюстрируют рис. 2.7 и: 2.4.

Предельная норма технического замещения факторов производства

Мерой взаимозаменяемости факторов производства служит предельная норма технического замещения MRTS (marginal rate of technical substitution), которая показывает, на сколько единиц можно уменьшить один из факторов при увеличении другого фактора на единицу, сохраняя выпуск неизменным. Предельная норма технического замещения труда капиталом

а предельная норма технического замещения капитала трудом

Величина MRTS факторов производства определяется их предельной производительностью. В этом можно убедиться на основе следующих рассуждений. При увеличении количества труда на L выпуск возрастает на L·MP_L, а уменьшение объема капитала на К снижает его на К·MP_K. Следовательно, увеличение количества применяемого труда полностью компенсирует сокращение объема капитала, если выполняется следующее равенство:

L·MP_L = К·MP_K

= MRTS_L,K.

(2.1)

Определим предельную норму замещения капитала трудом при технологии :

(2.2)

При графическом построении MRTS соответствует тангенсу угла наклона касательной к изокванте в точке, указывающей необходимые объемы труда и капитала для производства заданного объема продукции.

Как конкретно меняется значениеMRTS, можно увидеть, выполняя 2.5.

В некоторых видах хозяйственной деятельности труд и капитал вообще не могут заменить друг друга и должны использоваться в фиксированной пропорции: 1 рабочий - 2 станка, 1 самолет - 10 членов экипажа. В этом случае технология производства отображается производственной функцией Леонтьева⁴:

Q = min{L/a; K/b},

где a и b - технологически необходимый расход соответственно труда и капитала на единицу продукции.

Если, например, на каждом автобусе дальнего следователя должно быть два водителя, то при наличии в автобусном парке 50 автобусов и 90 водителей одновременно могут обслуживаться только 45 маршрутов: min{90/2;50/1} = 45. При технологии Леонтьева MRTS = 0.

Из равенства (2.1) следует, что при заданной технологии каждой величине капиталовооруженности труда (точке на изокванте) соответствует свое соотношение между предельными производительностями факторов производства. Иначе говоря, одной из специфических характеристик технологии является то, как сильно меняется соотношение предельных производительностей капитала и труда при небольшом изменении капиталовооруженности. Графически это отображается степенью кривизны изокванты. Количественной мерой этого свойства технологии является эластичность замещения факторов производства, которая показывает, на сколько процентов должна измениться капиталовооруженность труда, чтобы при изменении соотношения производительностей факторов на 1% выпуск остался неизменным. Обозначим K/L ψ; тогда эластичность замещения факторов производства

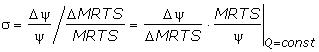С учетом равенства (2.2) легко заметить, что = 1 при технологии.

Кроме производственных функций Кобба - Дугласа и Леонтьева в экономическом анализе широко применяют производственную функцию с постоянной эластичностью замещения факторов производства CES (constant elasticity substitution).

У такой функции = 1/(1 -), т.е. эластичность замены постоянна, но не обязательно равна единице. Производственные функции Кобба - Дугласа и Леонтьева являются частными случаями функцииCES: если 0, то1, а еслиoo , то0.

Ломанная изокванта

По технологии Кобба - Дугласа заданный объем продукции можно произвести при любой капиталовооруженности труда, по технологии Леонтьева она однозначно задана. На практике эти два крайних варианта встречаются редко. Чаще всего заданный объем продукции можно произвести при ограниченном числе различных сочетаний труда и капитала. В этих случаях от изокванты остается лишь несколько точек. Но если существуют хотя бы два варианта выпуска заданного объема продукции с постоянным эффектом масштаба, то их можно применять одновременно, производя одну часть заданного выпуска по одному варианту, а оставшуюся по другому. В результате получим множество дополнительных вариантов производства заданного объема продукции. Это множество представляет отрезок, соединяющий точки двух исходных вариантов. Рассмотрим сказанное на примере рис. 2.8.

Смотрите также файлы

Савицкая - Лекции по микроэкономике - Глава 14.pdf

Савицкая - Лекции по микроэкономике - Глава 13.pdf

Савицкая - Лекции по микроэкономике - Глава 12.pdf

Савицкая - Лекции по микроэкономике - Глава 11.pdf

Савицкая - Лекции по микроэкономике - Глава 10.pdf

Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc

Смотрите также файлы

Информация

Списки файлов

Дополнительно