Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.09.2024
Просмотров: 714
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 3. Теория потребительского спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
Глава 5. Ценообразование на монополизированном рынке
Глава 9. Отказы рынка и аллокативная роль государства
Глава 10. Микроэкономика внешней торговли
Глава 1. Введение в микроэкономику
1.1. Микроэкономика как часть современной экономической теории
1.2. Методы экономического анализа
1.3. Логическая структура курса
Глава 2. Теория производства и предложения благ
2.1. Производственная функция и техническая результативность производства
2.2. Затраты производства и функция затрат
2.3. Прибыль и условия ее максимизации
2.4. Функция предложения и излишек производителя
Глава 3. Теория потребительского спроса
3.3. Эффект замены и эффект дохода
3.4. Компенсационное и эквивалентное изменения дохода и излишки потребителя 7
3.5. Выявление предпочтений потребителя
3.6. Рыночный спрос и эластичность спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
4.1. Отраслевое равновесие и его разновидности
4.2. «Паутинообразная» модель ценообразования
4.3. Величина равновесной цены
4.4. Особенности рынка совершенной конкуренции
4.5. Последствия государственного регулирования цен
Глава 5. Ценообразование на монополизированном рынке
5.1. Цена, максимизирующая прибыль
5.3. Цены, максимизирующие выручку и норму прибыли
5.4. Отсутствие функции предложения
5.5. Последствия государственного регулирования
Глава 6. Ценообразование на рынках несовершенной конкуренции
6.1. Монополистическая конкуренция
6.2.1. Олигополия на рынке гомогенного блага
6.2.2. Олигополия на рынке гетерогенного блага
6.3. Олигополия в свете теории игр
Глава 7. Ценообразование факторов производства
7.1. Предложение факторов производства
7.2. Спрос на факторы производства
7.3. Прокатная цена фактора производства
7.4. Функциональное распределение результатов производства
7.5. Капитальная цена фактора производства
Глава 8. Общее экономическое равновесие и общественное благосостояние
8.1. Цены частичного и общего равновесия
8.2. Модель общего экономического равновесия Вальраса
8.3. Конкурентное равновесие и общественное благосостояние
8.4. Первая теорема общественного благосостояния
8.5. Вторая теорема общественного благосостояния
Глава 9. Отказы рынка и аллокативная роль государства
9.2. Интернализация внешних эффектов
9.3. Производство общественных благ
9.4. Асимметричность информации
Глава 10. Микроэкономика внешней торговли
10.1. Основы международного разделения труда
10.1.1. Исходная модель Рикардо
|
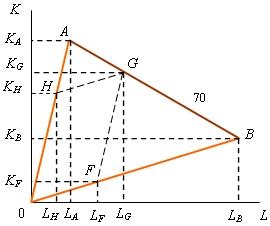
Произвести 70 ед. продукции можно используя либо KA и LA, либо KB и LB. Обе технологии имеют неизменный эффект масштаба. Если по технологии, представленной точкой А, произвести только 42 ед. продукции, то потребуется KH = 0,6KA единиц капитала и LH = 0,6LA единиц труда (точка Н). Оставшиеся 28 ед. произведем по технологии В. Необходимые для этого количества факторов производства можно определить следующим образом. Из точки Н проведем прямую, параллельную лучу 0В, до пересечения с отрезком АВ. Из точки их пересечения G проведем прямую, параллельную лучу 0А, до пересечения с лучом 0В. Точка пересечения F укажет искомые значения количества труда и объема капитала для производства 28 ед. продукции по технологии В. Так как по построению KF + KH = KG и LH + LF = LG, то точка G наряду с точками А и В представляет один из множества вариантов выпуска 70 ед. продукции. |
Изменение доли заданного выпуска, производимой по каждой из двух технологий А и В, на рис. 2.8 отображается скольжением точки Н по лучу 0А. Вслед за движением точки Н точка G будет перемещаться по отрезку АВ, указывая на общие объемы труда и капитала, необходимые для производства заданного выпуска одновременно по двум вариантам. Следовательно, каждая точка на отрезке АВ представляет сочетания определенных количеств труда и капитала, позволяющих произвести заданный объем продукции.
|
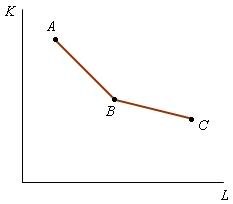
Поэтому, если, например, имеются только три варианта выпуска заданного объема продукции, представленные на рис. 2.9 точками A, B и С, то отрезки АВ и BС образуют ломанную изокванту. На этом закончим анализ технологического соотношения «input-output» («ресурсы-выпуск»), который необходим, но недостаточен для принятия фирмой решения относительно вида и масштаба производства. Экономический результат хозяйственной деятельности определяется на основе сопоставления объемов израсходованных факторов производства и выпущенной продукции в ценностном измерении. При этом используют понятия «затраты (издержки) производства», «выручка», «прибыль». |
2.2. Затраты производства и функция затрат
Затраты- это ценность материалов и услуг факторов производства, использованных при изготовлении продукции. Поскольку материалы, потребленные в данном процессе производства, ранее были изготовлены при использовании труда и капитала, то в итоге все затраты сводятся к оплате факторов производства.
Когда
объем производства превышает единицу,
тогда различают общие затраты ТС(total cost) на весь выпуск, средние затратыАС(average cost) на единицу продукции
(АС = TC/Q) и предельные затратыМС(marginal cost) - приращение общих
затрат при увеличении выпуска на единицу
(МС=![]() TC/
TC/![]() Q).
Q).
Зависимость между объемом произведенной продукции и минимально необходимыми для ее производства затратами называют функцией затрат.
Обозначим цену труда, т.е. количество денег, которое необходимо заплатить за использование наемного работника в течение определенного времени, rL, а цену капитала - количество денег, уплачиваемое за применение средств производства в течение некоторого времени, -rK. Тогда общие затраты на выпуск некоторого количества продукции:TC=rLL+rKK.
При заданных ценах факторов производства величина затрат определяется минимально необходимыми для выпуска продукции объемами труда и капитала, т.е. технологией, представленной производственной функцией Q = Q(L,K). ПоэтомуL = L(Q),K = K(Q), а следовательно, иTC = TC(Q).
Выделение
короткого и длинного периодов при
построении производственной функции
находит свое отражение и в функции
затрат. Поскольку в коротком периоде
К=![]() = const,
то функция затрат в этом случае имеет
видTC(Q) =rLL(Q) +rK
= const,
то функция затрат в этом случае имеет
видTC(Q) =rLL(Q) +rK![]() ,
т.е. в коротком периоде затраты делятся
на постоянныеTFC(total fixed cost), не
зависящие от объема выпуска (TFC=rK
,
т.е. в коротком периоде затраты делятся
на постоянныеTFC(total fixed cost), не
зависящие от объема выпуска (TFC=rK![]() ),
и переменныеTVC(total variable cost), меняющиеся
по мере изменения выпуска (TVC=rLL(Q)).
В длинном периоде все затраты переменные.
),
и переменныеTVC(total variable cost), меняющиеся
по мере изменения выпуска (TVC=rLL(Q)).
В длинном периоде все затраты переменные.
Переход от производственной функции к функции общих затрат осуществляется в приведенной ниже последовательности:
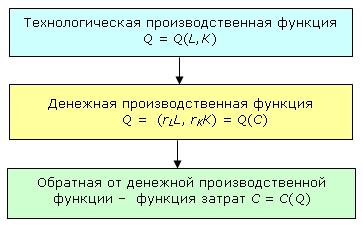
Выполним этот переход графически и алгебраически для короткого и длинного периодов.
Короткий период
|
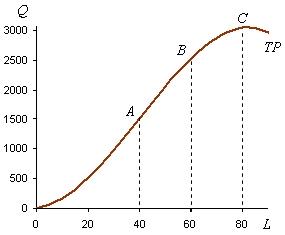
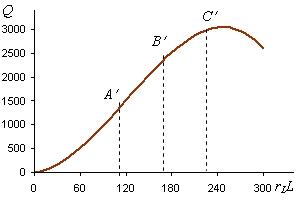
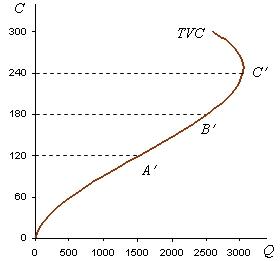
Возьмем за основу график общего выпуска в коротком периоде, представленный на рис. 2.10. Если на оси абсцисс откладывать не количество труда, а расходы на его оплату (rLL), то получим график денежной производственной функции общего выпуска, изображенный на рис. 2.11 при rL = 3.
Кривая
Q(rLC) |
|
|
|
|||||
|
|
|
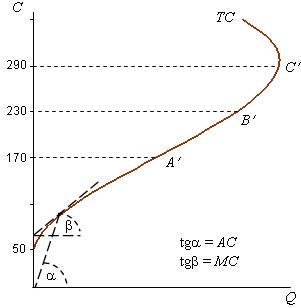
Так как график TFC по определению - это прямая, параллельная оси абсцисс, а ТС = TFC + TVC, то график общих затрат получается в результате параллельного сдвига кривой TVC вверх на величину общих постоянных затрат (рис. 2.13).
|
Тангенс
угла
По
изменениям tg
С |