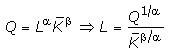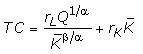Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.09.2024
Просмотров: 718
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 3. Теория потребительского спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
Глава 5. Ценообразование на монополизированном рынке
Глава 9. Отказы рынка и аллокативная роль государства
Глава 10. Микроэкономика внешней торговли
Глава 1. Введение в микроэкономику
1.1. Микроэкономика как часть современной экономической теории
1.2. Методы экономического анализа
1.3. Логическая структура курса
Глава 2. Теория производства и предложения благ
2.1. Производственная функция и техническая результативность производства
2.2. Затраты производства и функция затрат
2.3. Прибыль и условия ее максимизации
2.4. Функция предложения и излишек производителя
Глава 3. Теория потребительского спроса
3.3. Эффект замены и эффект дохода
3.4. Компенсационное и эквивалентное изменения дохода и излишки потребителя 7
3.5. Выявление предпочтений потребителя
3.6. Рыночный спрос и эластичность спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
4.1. Отраслевое равновесие и его разновидности
4.2. «Паутинообразная» модель ценообразования
4.3. Величина равновесной цены
4.4. Особенности рынка совершенной конкуренции
4.5. Последствия государственного регулирования цен
Глава 5. Ценообразование на монополизированном рынке
5.1. Цена, максимизирующая прибыль
5.3. Цены, максимизирующие выручку и норму прибыли
5.4. Отсутствие функции предложения
5.5. Последствия государственного регулирования
Глава 6. Ценообразование на рынках несовершенной конкуренции
6.1. Монополистическая конкуренция
6.2.1. Олигополия на рынке гомогенного блага
6.2.2. Олигополия на рынке гетерогенного блага
6.3. Олигополия в свете теории игр
Глава 7. Ценообразование факторов производства
7.1. Предложение факторов производства
7.2. Спрос на факторы производства
7.3. Прокатная цена фактора производства
7.4. Функциональное распределение результатов производства
7.5. Капитальная цена фактора производства
Глава 8. Общее экономическое равновесие и общественное благосостояние
8.1. Цены частичного и общего равновесия
8.2. Модель общего экономического равновесия Вальраса
8.3. Конкурентное равновесие и общественное благосостояние
8.4. Первая теорема общественного благосостояния
8.5. Вторая теорема общественного благосостояния
Глава 9. Отказы рынка и аллокативная роль государства
9.2. Интернализация внешних эффектов
9.3. Производство общественных благ
9.4. Асимметричность информации
Глава 10. Микроэкономика внешней торговли
10.1. Основы международного разделения труда
10.1.1. Исходная модель Рикардо
|
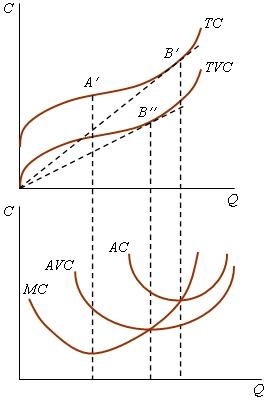
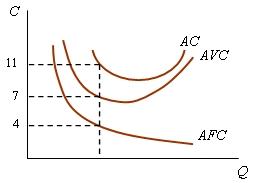
Трем особым точкам (а', b', c') соответствуют минимумы МС, AVC, AC. Обратим внимание на три обстоятельства. Во-первых, минимум AVC достигается при меньшей величине выпуска, чем минимум АС. Наглядно объяснить этот факт можно с помощью рис. 2.15, на котором кривая АС представлена как результат вертикального сложения кривых AFC = TFC/Q и AVC: до тех пор, пока снижение средних постоянных затрат перекрывает рост средних переменных затрат, увеличение выпуска после достижения минимума AVC сопровождается уменьшением средних затрат на единицу продукции.
В общей динамике затрат в коротком периоде можно выделить четыре фазы: 1) одновременное снижение предельных, средних переменных и совокупных средних затрат; 2) уменьшение средних переменных и совокупных средних при увеличении предельных затрат; 3) повышение предельных и средних переменных при снижении средних совокупных затрат; 4) одновременное увеличение всех видов затрат. |
|
Во-вторых, кривая МС всегда пересекает кривые AVC и АС в точке их минимума. Это объясняется тем, что добавление к выпущенному количеству продукции дополнительной единицы, произведенной с меньшими затратами, чем требовалось в среднем на предыдущий выпуск, ведет к снижению средних затрат. Если же ситуация складывается так, что дополнительная единица, произведена с большими затратами, то средние затраты увеличиваются. Но если при МС < AC (или AVC) они снижаются, а при МС > AC (или AVC) средние затраты возрастают, то МС = AC (или AVC) в точке минимума средних затрат. В-третьих, при любом заданном объеме выпуска сумма предельных затрат по определению равна сумме переменных затрат. |
Для
получения алгебраического представления
функции затрат примем, что производство
продукции осуществляется по технологии,
которая соответствует производственной
функции
![]() Если
объем капитала фиксирован, то
Если
объем капитала фиксирован, то
|
|
|
. |
|
Поэтому в коротком периоде общие затраты:
|
|
|
. |
(2.3) |
Первое слагаемое представляет переменные затраты, а второе - постоянные.
Длинный период
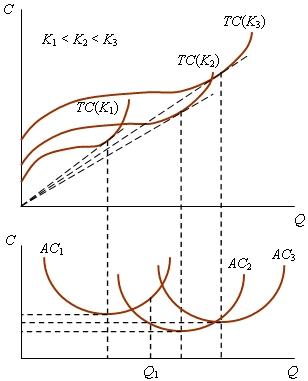
Аналогично тому, как производственную функцию длинного периода можно представить в виде множества производственных функций короткого периода, различающихся объемами постоянного фактора производства, затраты в длинном периоде можно изобразить посредством множества кривых затрат в коротком периоде, которые отличаются величиной постоянных затрат (рис. 2.16, верхняя часть).
|
По мере увеличения объема капитала растут постоянные затраты, сдвигая кривую TC вверх. В результате увеличения капиталовооруженности труда все больший объем продукции производится при снижающихся средних переменных затратах, что отображается удлинением участка кривой TC, загибающегося к оси абсцисс. В нижней части рис. 2.16 построены кривые средних затрат в коротком периоде, соответствующие кривым общих затрат. Чем больше объем капитала (постоянных затрат), тем правее расположена кривая АС, указывая на то, что по мере роста масштаба производства минимум средних затрат достигается при все большем объеме выпуска. Будет ли при увеличении масштаба производства минимум средних затрат снижаться, повышаться или оставаться неизменным, зависит от того, какой эффект масштаба присуща применяемой технологии. При его росте кривая АС смещается не только вправо, но и вниз относительно осей координат; при снижении этого показателя происходит сдвиг кривой АС вправо-вверх; в случае постоянного она смещается вправо параллельно оси абсцисс. Отрезки кривых TC и АС, расположенные выше точек их взаимного пересечения, не соответствуют определению функции затрат из-за того, что не представляют минимально возможные затраты на заданный выпуск. Так, для производства Q1 единиц продукции следует применять К2, а не К1 единиц капитала. Поэтому кривые затрат в длинном периоде образуются из участков кривых затрат в коротком периоде до их взаимного пересечения. |
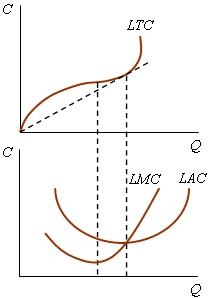
Если приращение капитала можно осуществлять маленькими порциями, то кривые общих LTC (long total cost) и средних затрат LAC (long average cost) в длинном периоде будут иметь, изображенный на рис. 2.17; кривая LMC (long marginal cost) представляет динамику предельных затрат.
|
Чтобы представить функцию затрат длинного периода с помощью производственной функции с взаимозаменяемыми факторами производства необходимо определить, при каком сочетании количества труда и объема капитала продукция производится с минимальными затратами. Если фирма может заплатить за покупку факторов производства М денежных единиц, то как распределить эту сумму между трудом и капиталом, чтобы при данной технологии выпустить максимально возможный объем продукции? При заданных ценах факторов производства область выбора фирмы задается равенством
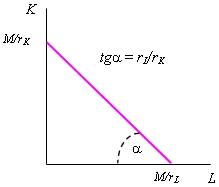
На рис. 2.18 эта область представлена прямой линией, называемой изокостой (линией равных затрат). Каждая ее точка показывает, какие количества труда и капитала фирма может купить при имеющихся деньгах.
Тангенс
угла ( |
|
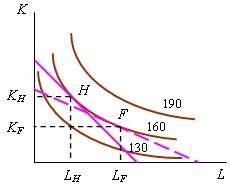
Технологические возможности фирмы в длинном периоде, как уже отмечалось, представляет карта изоквант. Проведя на ней изокосту, мы совместим технологические и финансовые возможности фирмы. Точка касания изокосты с наиболее отдаленной от начала координат изоквантой (рис. 2.19, точка Н) указывает на сочетание количества труда и капитала, обеспечивающее максимально возможный объем выпуска. Для большего выпуска у производителя не хватает средств: все изокванты большего выпуска расположены выше изокосты. Используя LH единиц труда и KH единиц капитала, фирма произведет 160 ед. продукции с минимальными затратами. Состояние, при котором фирма в длинном периоде производит продукцию с минимальными средними затратами, называют равновесием производителя. |
|
В точке касания изокванты с изокостой обе линии имеют одинаковый наклон. Как было установлено выше, наклон изокванты определяется предельной нормой технической замены капитала трудом, а наклон изокосты - отношением цен факторов производства. Следовательно, условием равновесия фирмы является следующее равенство: MRTSL,K = rL/rK. Поскольку MRTSL,K = MPL/MPK, то в длинном периоде продукция производится с минимальными затратами, если отношение предельных производительностей факторов производства равно отношению их цен:
|
Равенство (2.4) является условием равновесия конкурентной фирмы, из которого определяются объемы труда и капитала, используемые фирмой в длинном периоде.
|
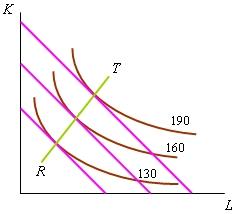
Если отношение цен факторов производства не изменяется, то любой объем продукции фирма производит при одной и той же капиталовооруженности труда, т.е. за счет изменения масштаба производства. Используемые ей объемы труда и капитала в этом случае определяются точками касания изоквант с перемещающейся параллельно самой себе изокостой рис. 2.20. Соединив все точки касания, получим линию (путь) развития фирмы (TR). Изменение относительных цен факторов производства приводит к изменению капиталовооруженности труда. Так, если в ситуации, представленной на рис. 2.19, снизится цена труда или повысится цена капитала, то наклон изокосты к оси абсцисс уменьшится и фирма будет производить 160 ед. продукции при сочетании LF, KF. Обратим внимание на то, что переход из точки H в точку F сопровождается снижением производительности труда: то же количество продукции производится с большими затратами труда. Тем не менее сочетание LF, KF обеспечивает минимум затрат на выпуск 160 ед. продукции в новой системе цен факторов производства. |
![]()
Чтобы
представить функцию затрат в длинном
периоде в алгебраическом виде решить
следующую задачу: найти такие значения L
и K,
удовлетворяющие равенству Q = L![]() K
K![]() ,
при которых сумма (rLL + rKK)
достигает минимума. Для этого воспользуемся
минимизацией функции Лагранжа
,
при которых сумма (rLL + rKK)
достигает минимума. Для этого воспользуемся
минимизацией функции Лагранжа
![]() = rLL + rKK -
= rLL + rKK - ![]() (L
(L![]() K
K![]() - Q),
- Q),