Добавлен: 21.10.2018
Просмотров: 1104
Скачиваний: 6
КОНТРОЛЬНАЯ РАБОТА ОБЩИЕ ТРЕБОВАНИЯ, ЗАДАНИЯ И ПОЯСНЕНИЯ К
ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Общие требования к оформлению контрольной работы
Контрольная работа должна быть выполнена с пронумерованными страницами и полями.
На титульном листе должны быть написаны фамилия студента, его инициалы, учебный
шифр, курс, полное название темы контрольной работы, дисциплина и номер варианта. В
конце работы следует указать список используемой литературы, дату выполнения работы
и подпись. Контрольная работа высылается для проверки в университет в срок,
установленный графиком. После получения проверенной работы необходимо внести
исправления и дополнения в соответствии с замечаниями преподавателя.
Заданиние №1
Теоритеческая часть
Метод «наихудшего» случая
Известно, что непрерывную и дифференцируемую функцию многих переменных можно
разложить в ряд Тейлора. Ряд Тейлора для отклонения функции с помощью дифференциалов
записывается в следующем впде:
!
3
/
)
(
!
2
/
)
(
)
(
)
(
)
(
3
2
i
i
i
i
i
i
x
f
d
x
f
d
x
df
x
f
dx
x
f
y
,
Где
)
(
),
(
),
(
3
2
i
i
i
x
f
d
x
f
d
x
df
-дифференциалы первого, второго, третьего порядка,
.
,
1 n
i
Отбрасывая члены ряда второго и выше порядков, получаем:
i
n
i
i
i
n
i
i
i
i
x
x
x
f
x
x
f
x
x
x
f
x
x
x
f
x
df
y
1
2
2
1
1
)
(
)
(
)
(
)
(
)
(
.
Здесь
i
i
i
A
x
x
f
i
)
(
-функция чувствительности, отражающая степень влияния входных
параметров
i
x
на выходной параметр
y
.
Функция чувствительности может быть как положительной, так и отрицательной величиной.
Сгруппируем их так, чтобы:
0
i
A
при
m
i
,
1
,
0
k
A
при
n
m
k
,
1
.
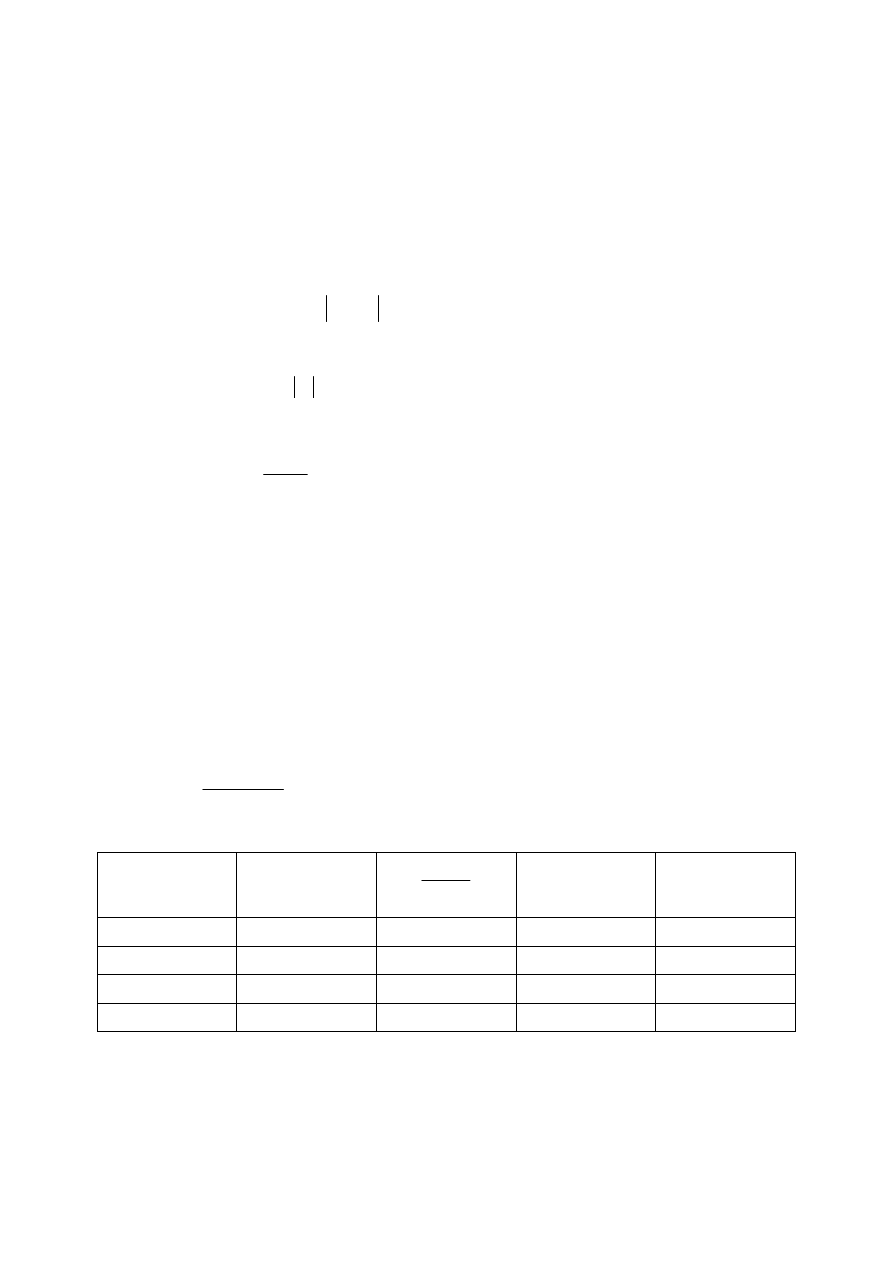
Тогда наихудшие отклонения выходных параметров вычисляются по формулам:
n
m
k
k
k
m
i
i
i
x
A
x
A
y
1
1
max
min
max
n
m
k
k
k
m
i
i
i
x
A
x
A
y
1
1
min
max
min
)
(
где A
i
>0 A
k
<0.
В случае симметричных отклонений входных параметров
min
max
i
i
i
x
x
x
пред
,
предельное отклонение выходного параметра
пред
i
n
i
i
пред
x
A
y
1
Для относительных отклонений выходного параметра справедливо:
y
y
y
пред
.
Если входные параметры являются случайными величинами, то дисперсия выходного параметра
определяется по формулам:
2
1
2
2
i
x
n
i
i
y
A
-для независимых между собой
i
x
и
n
i
k
i
n
k
ik
k
i
n
i
i
i
x
x
R
A
A
x
D
A
y
D
1
1
1
2
)
(
i
k
для зависимых
i
x
, где
ik
R
- коэффициенты парной корреляции.
Пример. Выходной параметр устройства f зависит от его внутренних параметров x
j
и задан
соотношением:
4
4
3
3
2
2
1
1
x
b
x
b
x
b
x
b
y
При этом заданы следующие величины:
Вариант №1
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=4
M(x
1
)=1.5
0.3
0.75
1.15
b
2
=5
M(x
2
)=1.75
0.3
0.75
1.15
b
3
=6
M(x
3
)=2
0.3
0.75
1.15
b
4
=7
M(x
4
)=2.5
0.3
0.75
1.15

Вариант №2
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=5
M(x
1
)=1
0.6
0.8
1.25
b
2
=6
M(x
2
)=1.5
0.6
0.8
1.25
b
3
=7
M(x
3
)=2
0.6
0.8
1.25
b
4
=8
M(x
4
)=2.5
0.6
0.8
1.25
Вариант №3
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=3
M(x
1
)=0.5
0.6
0.9
1.5
b
2
=4
M(x
2
)=0.75
0.6
0.9
1.5
b
3
=5
M(x
3
)=1
0.6
0.9
1.5
b
4
=6
M(x
4
)=1.25
0.6
0.9
1.5
Вариант №4
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=4
M(x
1
)=1.25
0.7
0.8
1.75
b
2
=5
M(x
2
)=1.5
0.7
0.8
1.75
b
3
=6
M(x
3
)=1.75
0.7
0.8
1.75
b
4
=7
M(x
4
)=2
0.7
0.8
1.75
Вариант №5
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=6
M(x
1
)=1
0.5
0.6
1.15
b
2
=7
M(x
2
)=1.25
0.5
0.6
1.15
b
3
=8
M(x
3
)=1.5
0.5
0.6
1.15
b
4
=9
M(x
4
)=1.75
0.5
0.6
1.15

Вариант №7
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=3
M(x
1
)=0.75
0.7
0.8
1.15
b
2
=4
M(x
2
)=1
0.7
0.8
1.15
b
3
=5
M(x
3
)=1.25
0.7
0.8
1.15
b
4
=6
M(x
4
)=1.5
0.7
0.8
1.15
Вариант №8
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=2
M(x
1
)=0.75
0.3
0.4
1.75
b
2
=3
M(x
2
)=1
0.3
0.4
1.75
b
3
=4
M(x
3
)=1.25
0.3
0.4
1.75
b
4
=5
M(x
4
)=1.5
0.3
0.4
1.75
Вариант №9
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=4
M(x
1
)=1.25
0.4
0.5
0.95
b
2
=5
M(x
2
)=1.5
0.4
0.5
0.95
b
3
=6
M(x
3
)=1.75
0.4
0.5
0.95
b
4
=7
M(x
4
)=2
0.4
0.5
0.95
Вариант №10
b
j
M(x
j
)
)
(
j
x
x
M
j
R
13
R
24
b
1
=5
M(x
1
)=0.5
0.2
0.3
1.15
b
2
=6
M(x
2
)=0.75
0.2
0.3
1.15
b
3
=7
M(x
3
)=1
0.2
0.3
1.15
b
4
=8
M(x
4
)=1.25
0.2
0.3
1.15

Получить количественные оценки точности выходного параметра.
1) Вычислим функцию чувствительности A
j
:
jнон
j
x
x
j
j
x
y
A
j=1…n
4
4
3
3
1
1
x
b
x
b
b
A
4
4
3
3
2
2
x
b
x
b
b
A
2
4
4
3
3
2
2
1
1
3
3
x
b
x
b
x
b
x
b
b
A
2
4
4
3
3
2
2
1
1
4
4
x
b
x
b
x
b
x
b
b
A
jнно
j
x
x
j
jj
x
y
A
2
2
j=1…n
A
11
=0
A
22
=0
3
4
4
3
3
2
2
1
1
2
3
33
2
x
b
x
b
x
b
x
b
b
A
3
4
4
3
3
2
2
1
1
2
4
44
2
x
b
x
b
x
b
x
b
b
A
kном
k
jном
j
x
x
x
x
k
j
jk
x
x
y
A
2
j=1…n, k=1…n, k
n
3
1
A
24
A
2) Вычислим математическое ожидание M(y) и дисперсию D(y) выходных параметров.
)
,...,
(
)
(
1
nнно
ном
x
x
f
y
M
n
j
j
jj
n
j
k
j
n
j
k
jk
jk
x
D
A
x
x
R
A
1
1
2
1
2
1
j
k,
где второе слагаемое учитывает нелинейность функции.