Файл: Основные структуры алгоритмов: сравнительный анализ и примеры их использования (Теоретические понятия алгоритмов).pdf

Рисунок 1 - Линейная структура алгоритма

- разветвленная структура алгоритма, содержит в себе как последовательности, так и распараллеливания последовательностей. Используется, когда в зависимости от условия необходимо выполнить то или иное действие (рис. 2, а), осуществить обход, если одна ветка не содержит никаких действий (рис. 2, б), осуществить множественный выбор, когда условие имеет более трех возможных вариантов (рис. 2, в).

Разветвленной называется конструкция, которая обеспечивает выбор между двумя альтернативами в зависимости от значения входных данных. Разветвленный алгоритм - это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.

Часто при решении задач приходится проверять одно условие для нескольких значений или повторять некоторые действия несколько раз.

Рисунок 2 - Виды разветвленной структуры алгоритмов

- циклическая, которая используется при необходимости выполнять некоторые действия несколько раз. Возможно исполнение цикла До, цикла Пока, цикла по параметру (рис. 3).

Рисунок 3 - Циклическая структура алгоритма

Особенностью всех приведенных структур является то, что они имеют один вход и один выход, поэтому их можно сочетать друг с другом в любой последовательности. Проанализируем приведенные алгоритмические структуры более детально.

Любой алгоритм содержит описание команд и определяет последовательность их выполнения. На первый взгляд, кажется, что все команды алгоритма всегда выполняются одна за другой, однако это не так. Для обеспечения такого свойства алгоритма, как массовость, его строят с учетом любого набора допустимых входных данных. Поэтому во многих случаях нельзя заранее предусмотреть, каким должен быть следующий шаг алгоритма. Отсюда возникает потребность в таких инструкциях исполнителю, которые позволят управлять его действиями по сложившейся ситуации в процессе выполнения алгоритма.

По характеру управления различают три основных вида структуры алгоритмов: линейные, с разветвлением и с повторением (циклический).

В простейшем случае алгоритм приписывает единовременное выполнение всех по очереди заданных действий независимо от значений входных данных задачи. Например, для нахождения объема призмы нужно найти площадь ее основания, определить высоту призмы, найти их произведение. Эти действия нужно выполнить для расчета объема любой призмы.

---

Сложнее с управлением справляются алгоритмы, которые предусматривают два возможных варианта действий.

Выбор варианта связывается с некоторым условием. Например, алгоритм решения квадратного уравнения подразумевает сначала нахождение значения дискриминанта, а затем, в зависимости от знака, или вывод сообщения об отсутствии действительных корней (если значение дискриминанта отрицательное), или нахождение их по соответствующим формулам (в противном случае).

Алгоритм, который подразумевает выполнение тех или иных действий в зависимости от результата проверки условия, называется алгоритмом с разветвлением, или разветвленным.

Хотя такой алгоритм содержит описание действий для обоих возможных вариантов, при каждом его выполнении реализуется только один из них, который именно - зависит от заданного набора входных данных. Итак, в отличие от линейного алгоритма, алгоритм с разветвлением приписывает выполнение не всех без исключения действий, а только тех, которые выбраны по условию.

Третий вид алгоритмов составляют алгоритмические процессы предусматривающие возможность повторного выполнения определенной последовательности действий.

Например, для подсчета суммы двух целых чисел (в столбик) необходимо сначала вычислить сумму последних цифр чисел-слагаемых, записать последнюю цифру результата и перенести, если нужно, единицу в следующий разряд. Далее по аналогичному правилу нужно вычислить сумму предпоследних цифр чисел-слагаемых и т. д. Процедура повторяется, пока все цифры чисел не будут исчерпаны. Количество повторений зависит от количества цифр в заданных числах.

Алгоритм, который приписывает повторное выполнение действий, называется алгоритмом с повторением, или алгоритмом с циклом (циклический). Повторяющееся действие или группа действий называется телом цикла. Количество повторений тела цикла определяется поставленным условием, которое называется условием цикла. По результатам проверки условия осуществляется выбор: еще раз повторить тело цикла или перейти к другим действиям.

Циклический алгоритм состоит из следующих этапов:

1. Подготовка цикла – осуществление действий, которые связаны с исходными данными;

2. Описание тела цикла – осуществление многократных действий для вычисления искомых величин, а также создание значений, необходимых для повторного выполнения действий в теле цикла;

3. Условия продолжения цикла - действия, которые определяют необходимость дальнейшего выполнения тела цикла.

---

Наличие возврата к ранее выполненным действиям является характерным отличием алгоритмов с циклами от линейных и разветвленных.

Все рассмотренные нами базовые алгоритмические структуры - линейная, разветвление, повторение - являются замкнутыми, каждая из них имеет один вход и один выход. Это позволяет рассматривать базовые структуры как целостные единицы и использовать любую из них как элемент другой. Другими словам, базовые структуры можно соединять последовательно и вкладывать друг в друга.

Например, в базовой структуре следования (рис. 4) функциональный блок Действие 1 может быть замещен разветвлением, а блок Действие 2 - повторением. Такое замещение можно продолжать дальше и дальше.

Рекурсивным называется алгоритм, который в ходе работы на любом шаге прямо или косвенно вызывает сам себя.

При решении многих задач применяется особый набор стандартных приемов алгоритмизации. Среди них выделим и проанализируем те, которые наиболее широко применяются при решении задач на практике.

1. Комбинированные алгоритмы. При решении задач достаточно часто происходит так, что алгоритм их решения подразделяется на части, фрагменты и каждая часть является алгоритмом одного из трех описанных выше типов. Алгоритм, который содержит несколько структур одновременно, называется комбинированным.

Все перечисленные алгоритмические структуры или же их комбинации могут быть использованы при составлении алгоритма сложной задачи.

1. Вложенные циклы. Отдельным случаем комбинированных алгоритмов являются алгоритмы, в которых необходимо задействовать несколько видов циклов, которые одновременно сменяются друг за другом. Например, внутри одного цикла могут находиться один или несколько других циклов. Такие комбинации носят название вложенный цикл. Охватываемый цикл называется внешним, а вложенные в него циклы - внутренними (вложенными), при этом область действия внутреннего цикла должна полностью находиться в области внешнего цикла, то есть циклы не могут мешать работе друг друга.

Алгоритм, сконструированный исключительно из базовых структур, называется структурным.

Теоретически доказано, что для задачи любой логической сложности можно сконструировать структурный метод.

Действие 1

Действие 2

Рисунок 4 - Базовая структура следования

Это доказательство является очень важным. Ведь оказывается, что из кирпичиков трех видов мы можем составлять любую архитектурную постройку. Отсюда открывается путь и к овладению программированием. Первым шагом на этом пути является овладение средствами представления базовых структур в программах.

---

3. Примеры применения структур алгоритмов

В данном разделе рассмотрим примеры применения основных базовых структур алгоритмов - линейные, разветвляющиеся, циклические на примерах решения конкретных практических задач.

Пример 1: Вычислите , где ; a=-7,25; b=2,05.

Линейная структура алгоритма (рис. 5):

конец

Вывод y

Ввод:

Ввод a, b

начало

Рисунок 5 - Линейная структура алгоритма

Код программы на языке Паскаль АБС.NET:

var x, y,a,b: real;

begin

a := readlnreal('a = ');

b := readlnreal('b = ');

y := sqrt((x*x+ sin(x)*sin(x))) / (power(4,x)+2);

x:= power(0.5,(a*a+1)*cos(b)*cos(b));

writeln('y = ', y)

end.

Результаты работы программы (рис. 6):

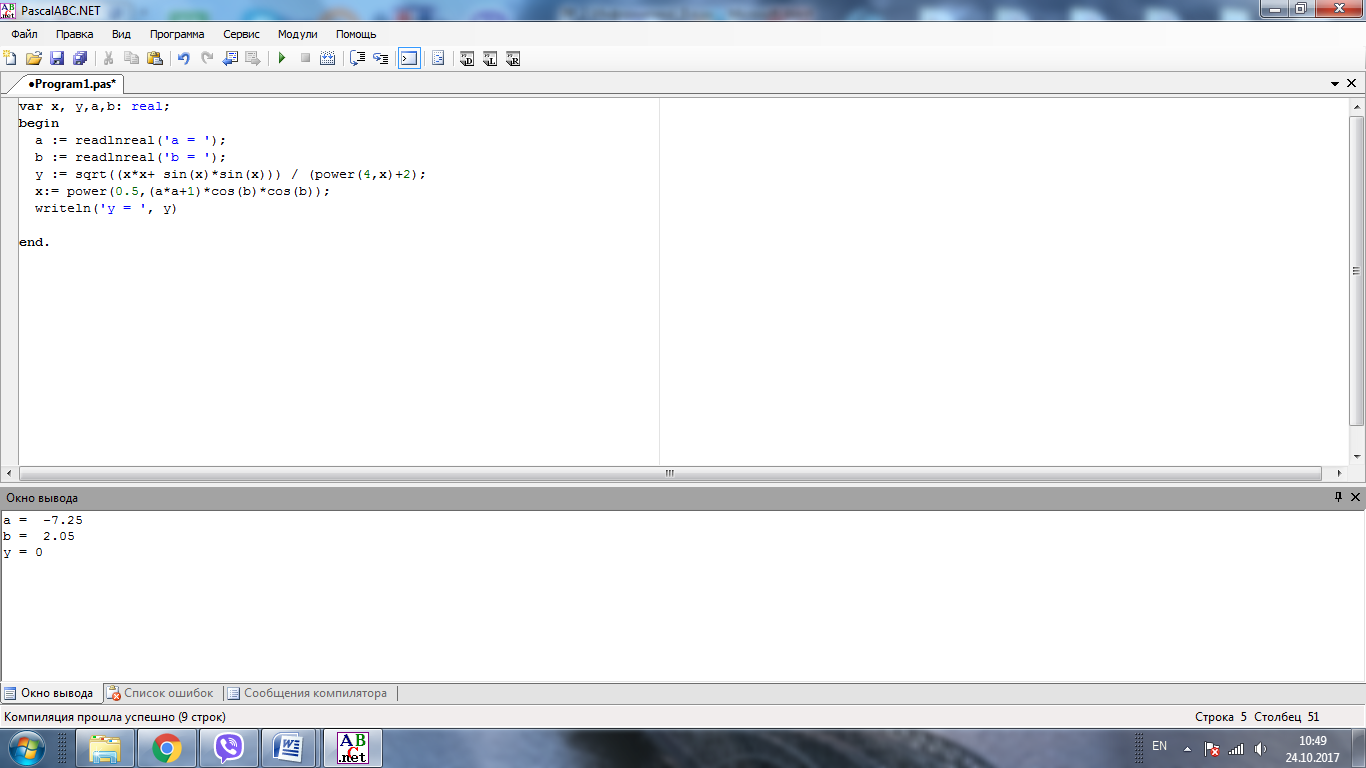
Рисунок 6 - Результат работы программы линейной структуры

Пример 2: Написать программу для нахождения значения y с использованием операторов IF (разветвленная структура алгоритмов). Выражения для вычисления значения выражений оформить.

Вычислить значение функции y для произвольного значений x .

Разветвленная структура алгоритма представлена на рисунке 7. Код программы на языке Паскаль АБС.NET:

var x:integer;

y:real;

begin

WriteLn('Введите Х');

ReadLn(x);

If (x<=3) and (x>=0) then

y:= x*x+1

else

If (x<0) and (x>3) then

y:= sin(3*x);

WriteLn(y);

end.

Рисунок 7 - Пример разветвленной структуры алгоритма

Результаты работы программы представлены на рисунке 8.

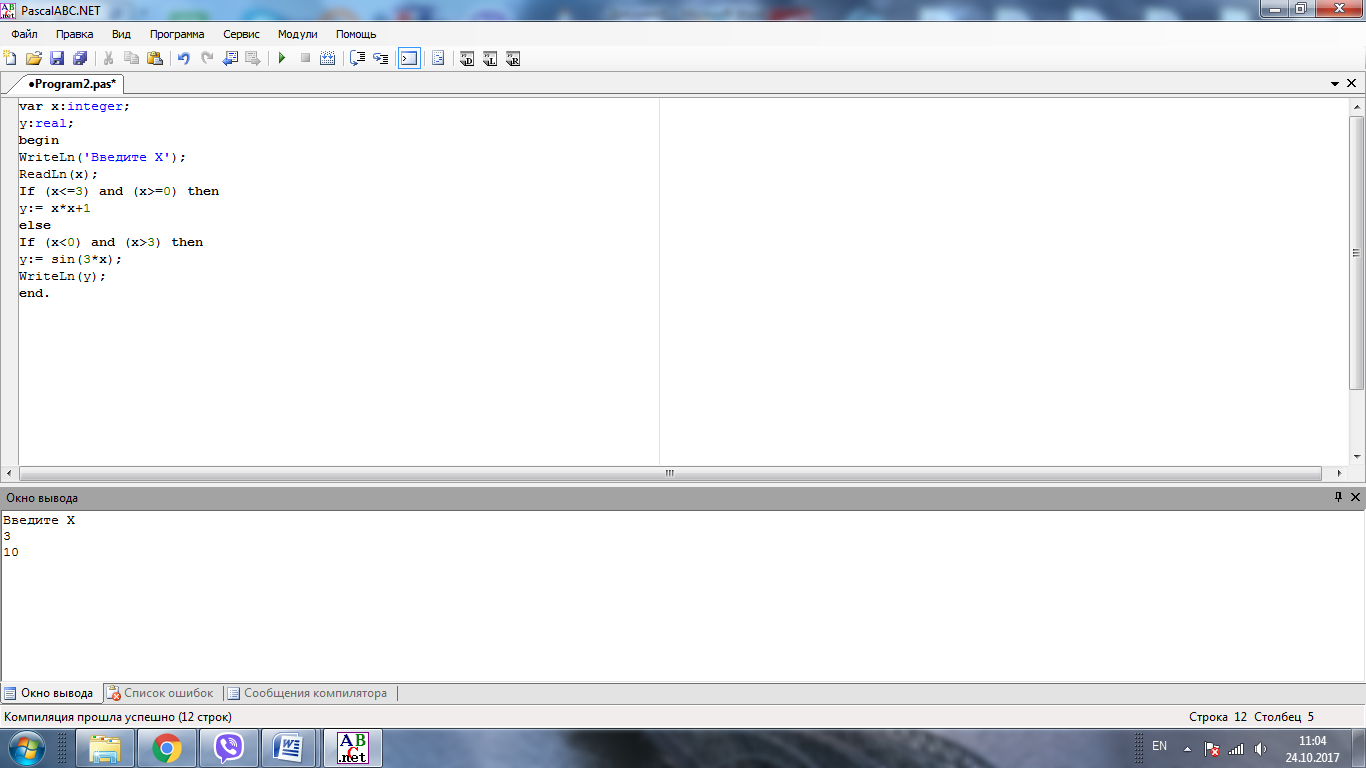
Рисунок 8 - Результат работы программы разветвленной структуры алгоритма

Пример 3: Вычислить произведение первых N натуральных чисел, делящихся на К.

Циклическая структура алгоритма представлена на рисунке 9.

Рисунок 9 - Циклическая структура алгоритма

Код программы на языке Паскаль АБС.NET:

var summa, n, k, i:integer;

---

begin

write('N равно: ');

readln(n);

write('K равно: ');

readln(k);

for i:=1 to n do

begin

if i mod k = 0 then

summa:=summa+i;

end;

writeln('Сумма первых N чисел кратных K равна: ', summa);

end.

Результат программы представлен на рисунке 10.

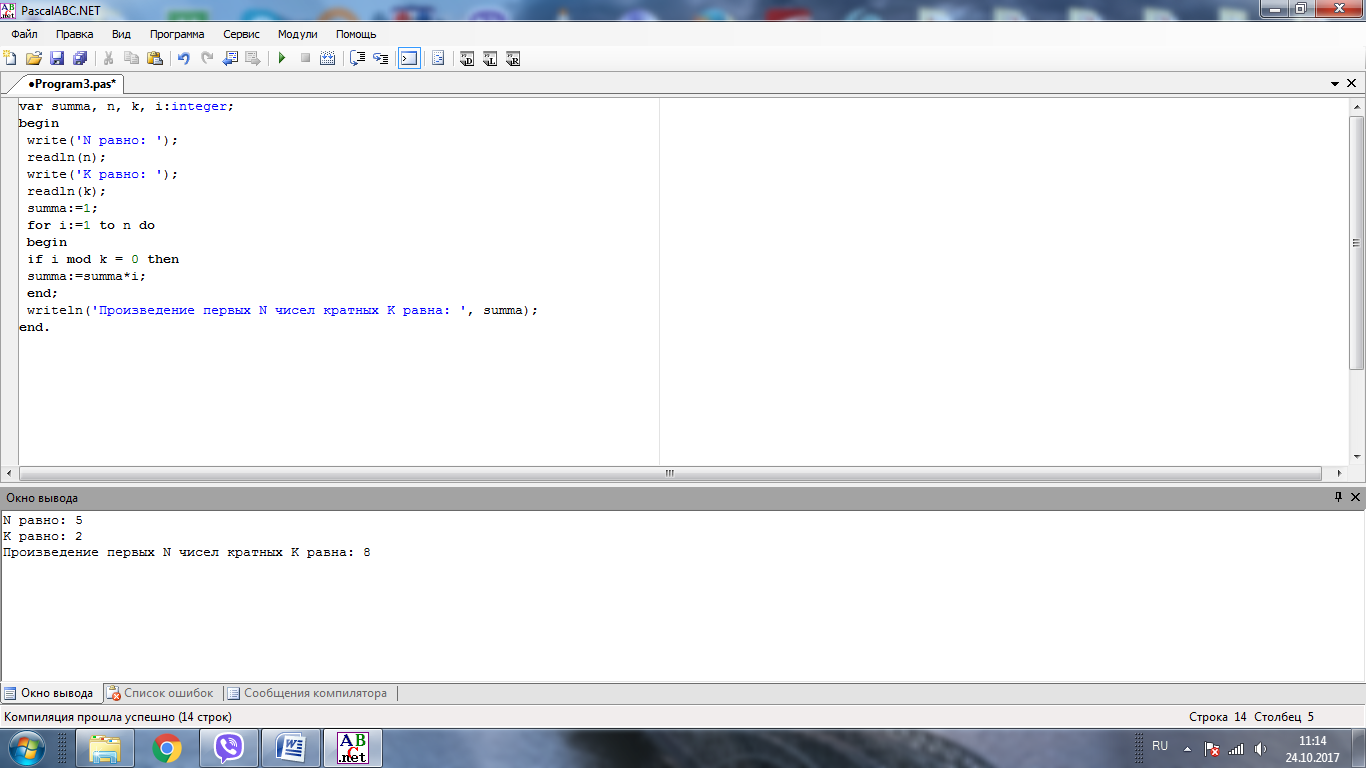
Рисунок 10 - Результат работы циклической структуры алгоритма

Пример 4: Составить таблицу значений: , h=0,1.

В данной задаче рассматривается комбинация разветвляющейся и циклической структуры алгоритмов.

Комбинированная структура представлена на рисунке 11. Код программы на языке Паскаль АБС.NET:

program v11;

var y, x: real;

begin

x:= -1;

while x<=1 do

begin

y:= sin (x)+(cos(x)/sin(x))-x;

writeln (x, ' | ',y:2:3);

x:=x+0.1;

end;

writeln;

writeln ('y=',y:2:3);

end.

Рисунок 11 - Комбинированная структура разветвляющегося и циклического алгоритмов

Результат работы программы представлен на рисунке 12.

Рисунок 12 - Результат работы программы

Пример 5: Используя разветвляющуюся структуру, составить блок-схему вычисления значения составной функции, имеющей различный вид на разных участках аргумента, затем составить программу, реализующую данный алгоритм (значение аргумента функции вводится с клавиатуры).

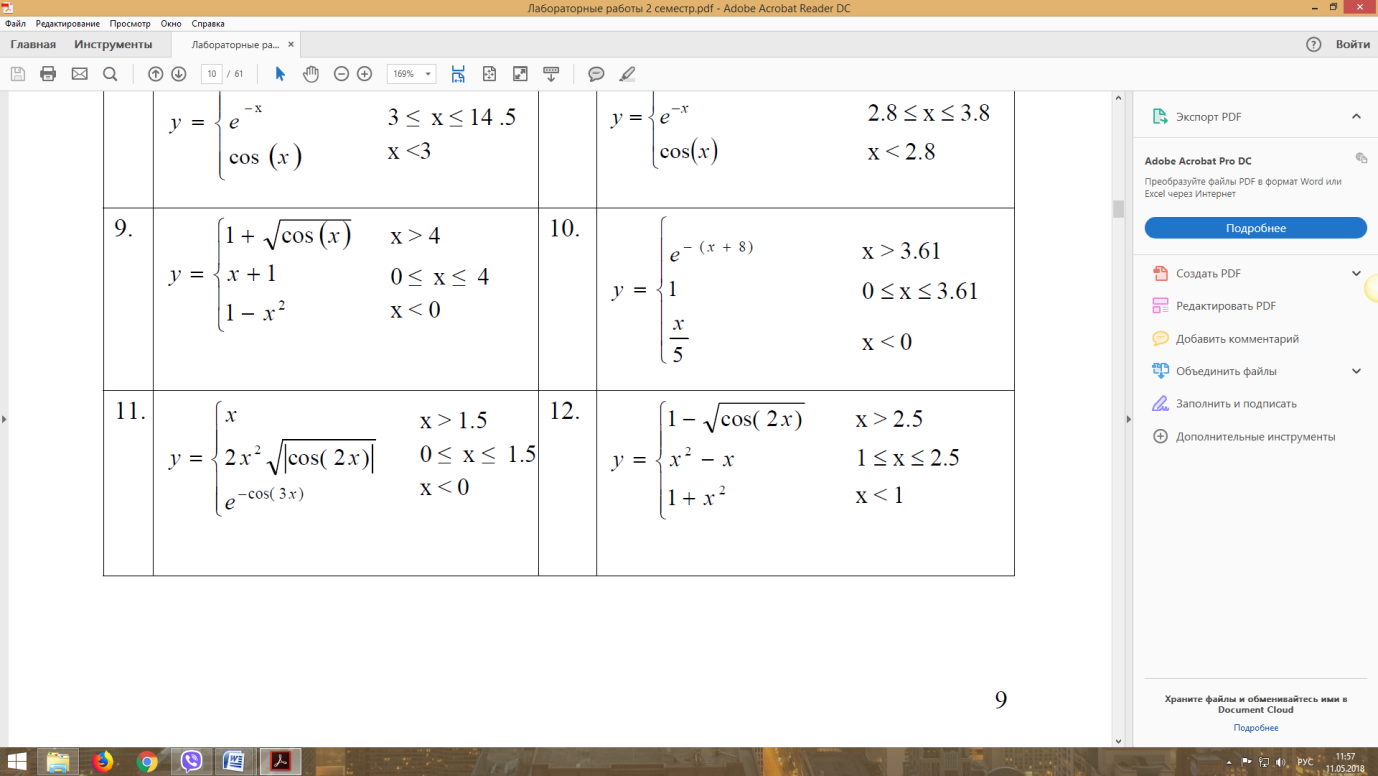
Разветвляющая структура алгоритма решения данной задачи представлена на рисунке 13.

Рисунок 13 - Разветвляющаяся алгоритмическая структура

Код программы на языке Паскаль АБС.NET:

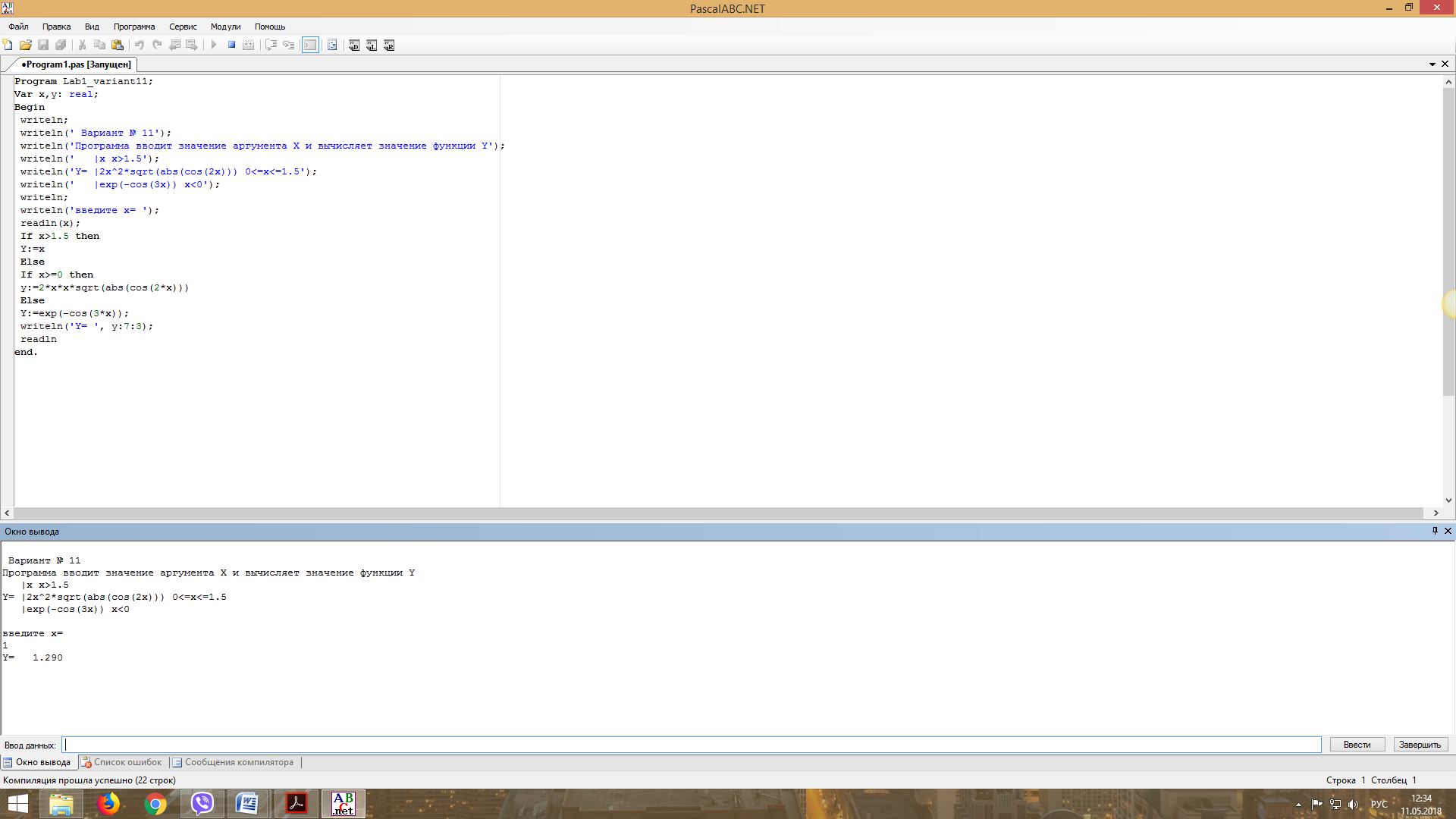
Program P1;

Var x,y: real;

Begin

writeln;

writeln('Программа вводит значение

аргумента X и вычисляет значение функции Y');

writeln(' |x x>1.5');

writeln('Y= |2x^2*sqrt(abs(cos(2x))) 0<=x<=1.5');

writeln(' |exp(-cos(3x)) x<0');

writeln;

writeln('введите x= ');

readln(x);

If x>1.5 then

Y:=x

Else

If x>=0 then

y:=2*x*x*sqrt(abs(cos(2*x)))

Else

Y:=exp(-cos(3*x));

writeln('Y= ', y:7:3);

readln

end.

Результат работы программы представлен на рисунке 14.

---