ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Проектирование информационных систем
Добавлен: 21.10.2018
Просмотров: 10771
Скачиваний: 8

76
Слово
ABSTRACTION
заменяется
ключевым
словом
PROCEDURE
и
добавляется
атрибут
RETURN(POINTER)
.
Кро-
ме
того,
используются
следующие
операторы:
declare
DUMMY POINTER;
ALLOCATE datatype SET(DUMMY);
Эти
операторы
позволяют
автоматически
распределять
память
для
данных
абстрактного
типа.
Для
того
чтобы
обеспе-
чить
возврат
из
подпрограммы
распределения
памяти
к
соот-
ветствующему
оператору
declare
,
перед
первым
оператором
FUNCTION
помещают
оператор
RETURN(DUMMY)
.
Вместо
опе-
ратора
REP
объявляется
структура
типа
BASED
.
Таким
образом,
транслятор
транслирует
следующие
операторы:
STACK: procedure RETURNS(POINTER);
declare 1 STACK BASED(X),
2 ENTRIES(100) FIXED,
2 TOPOFSTACK FIXED;
declare DUMMY POINTER;
ALLOCATE STACK SET(DUMMY);
TOPOFSTACK = 0;
return(DUMMY);
end
;
Вместо
оператора
FUNCTION
подставляется
последова-
тельность
ENTRY
BEGIN
.
Для
соответствующих
операторов
END
добавляются
операторы
RETURN
.
Таким
образом,
имеем:
STACK: procedure RETURNS(POINTER);
declare
1 STACK BASED(X),
2 ENTRIES(100) FIXED,
2 TOPOFSTACK FIXED;
declare DUMMY POINTER;
ALLOCATE STACK SET(DUMMY);
TOPOFSTACK = 0;
return(DUMMY)
PUSH: function(X,
элемент);
...
return;
end;
77
POP: function(X,
элемент);
...
return;
end;
...
end
;
Доступ
к
данным.
При
указанном
способе
организации
данных
защитные
меры
приняты
лишь
отчасти:
модуль
не
мо-
жет
получить
представление
любой
переменной
абстрактного
типа,
определенное
в
некотором
другом
модуле.
Однако
должен
ли
вообще
данный
модуль
иметь
доступ
к
определенным
дан-
ным
абстрактного
типа?
Окончательная
версия
программы
име-
ет
следующую
структуру:
Модуль
1
Модуль
2
…
Модуль
n
При
такой
структуре
программы
каждый
модуль
может
пользоваться
любой
функцией
любого
другого
модуля.
Однако
это
может
оказаться
нежелательным.
Предположим,
что
модуль
X
использует
абстрактный
тип
данных
Y,
который,
в
свою
оче-
редь,
обращается
к
абстрактному
типу
данных
Z
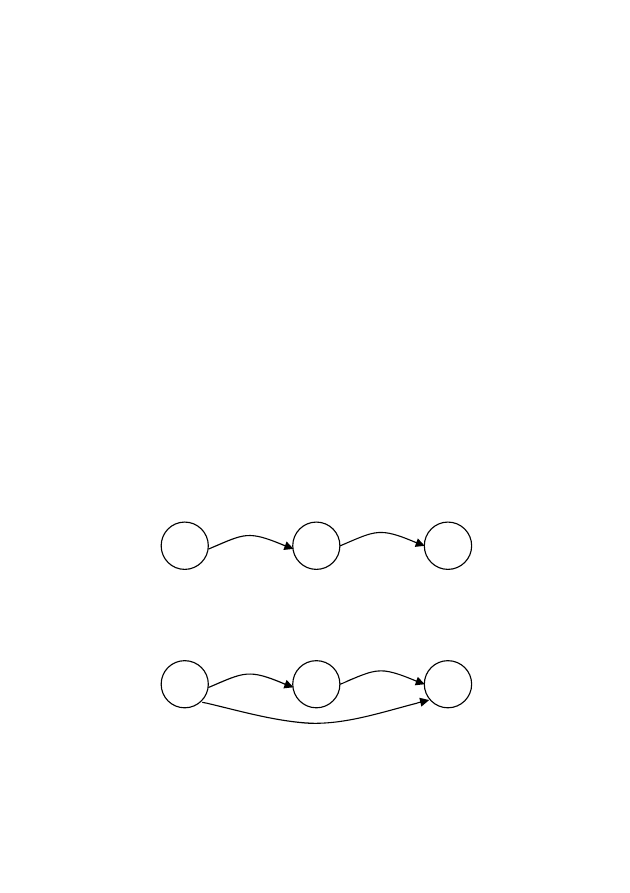
(рис.
4.14).
Рис.
4.14
—
Нарушение
принципа
информационной
локализованности
X
Y
Z
Х
известно
о
Y
;
Y
известно
о
Z
;
Х
неизвестно
о
Z
а
X
Y
Z
Х
вызывает
Z
непосредственно
б

78
При
написании
программы
программист,
стремясь
к
большей
эффективности
программы,
записывает
вызов
из
мо-
дуля
Х
данных
Z,
тем
самым
неумышленно
нарушает
специфи-
кацию
относительно
того,
что
о
структуре
данных
Z
известно
только
в
модуле
Y.
Однако
компилятор
не
в
состоянии
прове-
рить
это
нарушение,
а
ошибка
может
быть
выявлена
гораздо
позже,
например,
если
модуль
Y
когда-либо
изменится.
В
операционных
системах
имеется
возможность
защиты
от
некорректных
действий;
такую
форму
защиты
можно
доба-
вить
в
языки
программирования.
В
операционных
системах
имеется
вектор
возможностей,
связанный
с
каждым
независи-
мо
выполняемым
процессом.
Этот
вектор
описывает
функции,
которые
может
выполнять
данный
процесс.
Так
как
процессы
начинаются
и
заканчиваются,
когда
задания
пользователя
соот-
ветственно
поступают
в
систему
или
выходят
из
нее,
вектор
возможностей
динамичен,
и
производится
проверка
правомер-
ности
операций
во
время
работы
системы.
В
языках
программирования
аналогом
такого
вектора
яв-
ляется
право
доступа.
По
сравнению
с
вектором
возможностей
права
доступа
обладают
одним
значительным
преимуществом:
проверка
производится
во
время
компиляции,
а
не
во
время
вы-
полнения
программы.
Программа
статична,
все
ее
процедуры
известны
до
начала
выполнения,
все
абстрактные
типы
данных
известны,
и
проверка
правильности
обращения
к
данным
может
быть
выполнена
компилятором.
Заметим,
что
цель
использования
прав
доступа
заключа-
ется
в
ограничении
доступа
к
абстрактным
типам
данных,
а
не
в
обеспечении
безопасности
системы.
Предполагается,
что
про-
граммист
может
обращаться
ко
всем
элементам
системы,
по-
этому
права
доступа
могут
изменяться.
Контрольные
вопросы
1.
Язык
проектирования
программ
PDL.
Операторы
вы-
бора.
Операторы
цикла.
Операторы
описания
данных.
Операторы
ввода/вывода
и
вызова
процедур.
Оператор
leave
.
Предложения
на
естественном
языке.
2.
Нисходящее
проектирование
и
нисходящая
разработка.

79
3.
Пошаговое
совершенствование.
4.
Восходящее
проектирование.
5.
Подыгрывающие
программы
(заглушки).
6.
Структурное
проектирование.
Простая
программа.
Элементарная
программа.
Управляющие
структуры,
способы
их
описания.
7.
Скалярные
и
агрегативные
типы
данных.
8.
Массивы.
Структуры.
Списки.
Очереди.
Стеки.
Мно-
жества.
Графы.
Деревья.
9.
Абстрактные
конструкции.
10.
Фиксированные
данные
абстрактного
типа.
11.
Размещение
указателей.
12.
Защита
данных
от
несанкционированного
доступа.

80
5
ПРАВИЛЬНОСТЬ
ПРОГРАММ
Одним
из
важных
методов
повышения
эффективности
проектирования
программ
является
верификация
программ
или
математическое
доказательство
того,
что
программа
работает
правильно.
Для
доказательства
правильности
программ
исполь-
зуется
аксиоматический
подход,
при
котором
применяется
тео-
рия
перечисления
предикатов.
Предполагается,
что
каждый
оператор
в
программе
выполняет
заранее
определенные
дейст-
вия,
зависящие
только
от
синтаксиса
языка.
Для
двух
предика-
тов
P
и
Q
и
оператора
S
необходимо
определить,
истинно
ли
выражение:
«Если
P
истинно
и
если
выполняется
оператор
S,
то
Q
ис-
тинно».
Предикат
P
является
спецификацией
правильного
выпол-
нения
оператора
S,
а
предикат
Q
будет
истинным
после
выпол-
нения
оператора
S
и
является
спецификацией
следующего
за
S
оператора.
Если
это
утверждение
распространить
на
все
операторы
программы
и
если
P
является
спецификацией
первого
операто-
ра,
а
Q
истинно
после
окончания
программы,
то
будет
доказана
правильность
всей
программы
относительно
предикатов
P
и
Q.
Эту
конструкцию
можно
записать
в
следующем
виде:
{ } { }
,
P S Q
где
P
называется
предусловием
истинности
Q
после
выполне-
ния
программы
S.
Доказательство
правильности
программы
заключается
в
определении,
является
ли
выражение
{P}S{Q}
истинным
отно-
сительно
входных
спецификаций
P,
выходных
спецификаций
Q
и
операторов
S
программы.
Если
{P}S{Q}
истинно,
то
это
означает,
что
доказана
правильность
программы
S
относительно
P
и
Q.
5.1
Аксиомы
Для
целей
доказательства
правильности
программ
к
пра-
вилам
исчисления
предикатов
следует
добавить
правила,
необ-
ходимые
для
выполнения
последовательности
операторов
про-