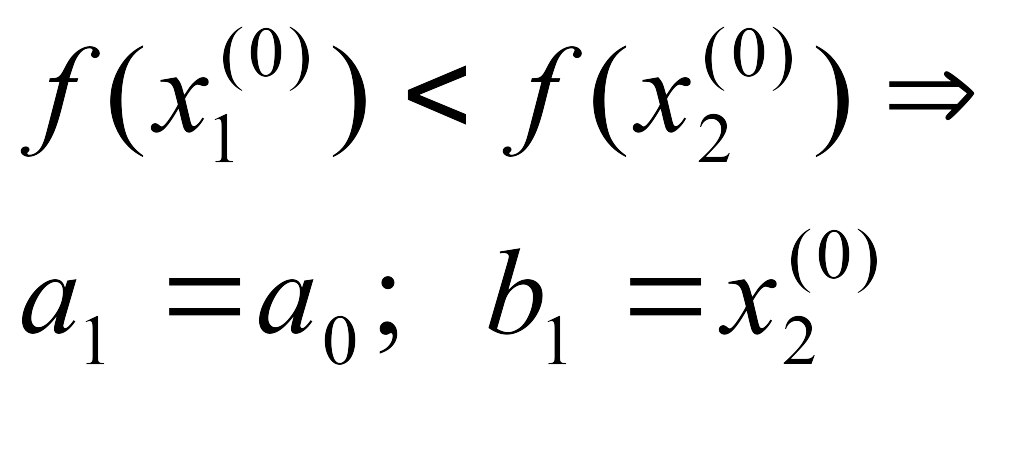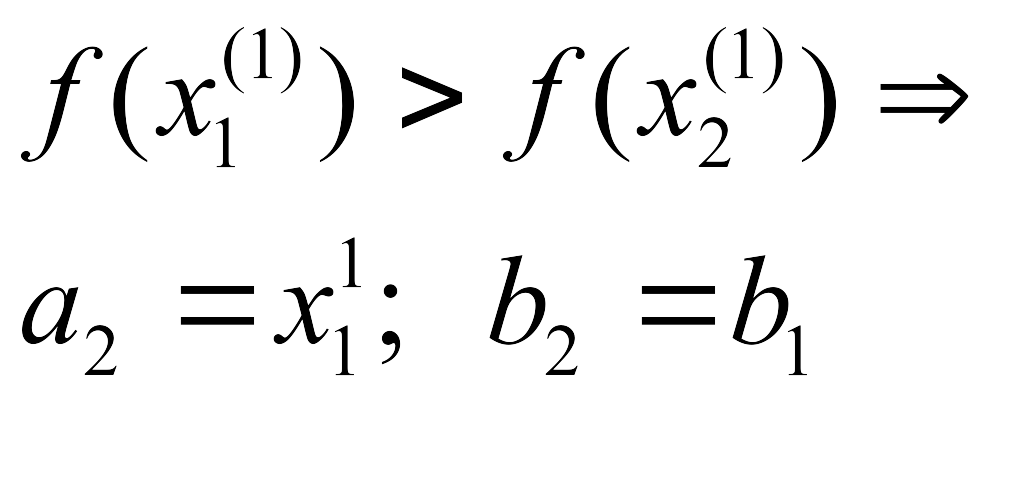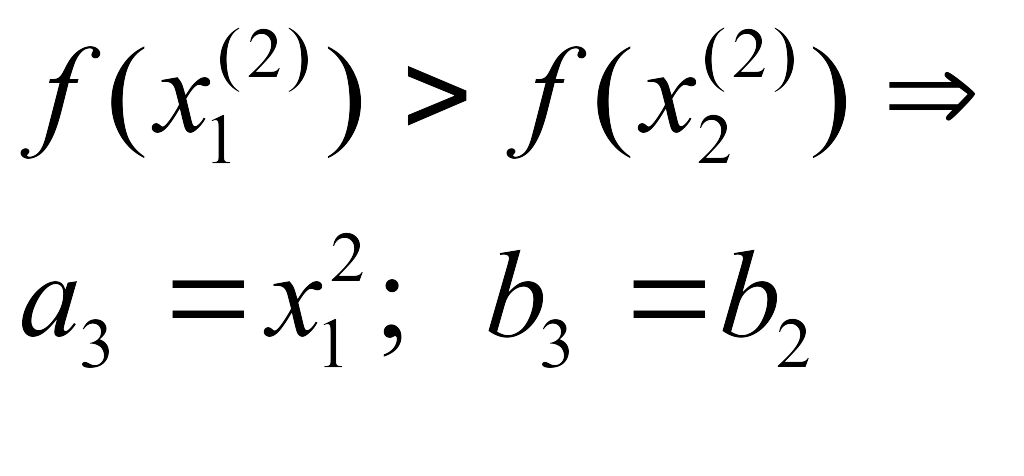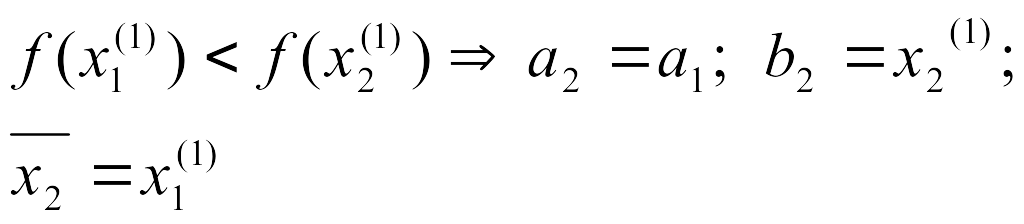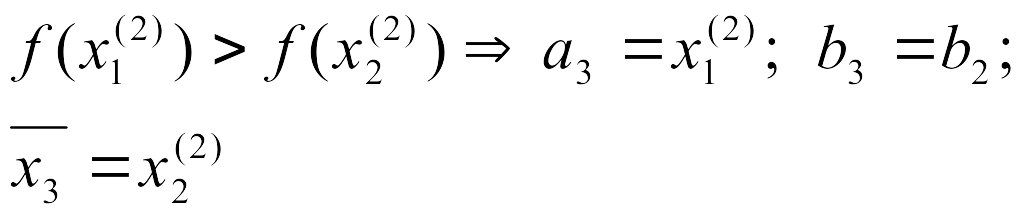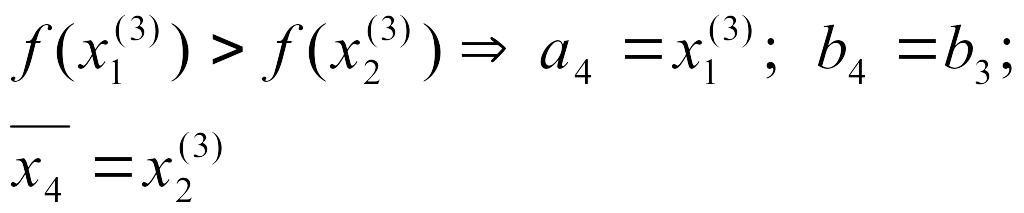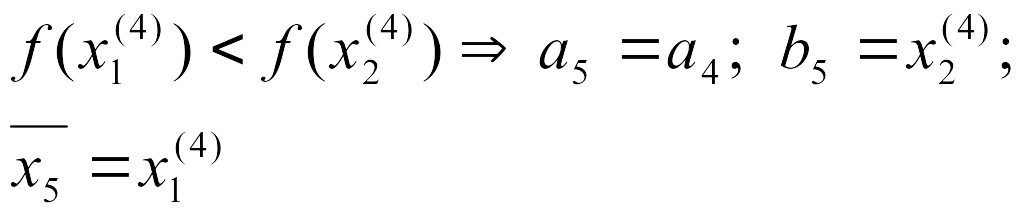ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Методичка
Дисциплина: Методы оптимизаций
Добавлен: 21.10.2018
Просмотров: 813
Скачиваний: 9
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
в![]() ысшего
образования
ысшего
образования
Пермский национальный исследовательский
политехнический университет
Чайковский филиал
Кафедра автоматизации, информационных и инженерных технологий
МП.12.8-2017
Методические предписания
к выполнению контрольной работы
по дисциплине
«Теория оптимизации»
для студентов заочной формы обучения
Направление подготовки 13.03.02 Электроэнергетика и электротехника
2017
Методические предписания к выполнению контрольной работы по дисциплине «Теория оптимизации».
Составитель: ст. преподаватель кафедры автоматизации, информационных и инженерных технологий ЧФ ПНИПУ Лабутина Т.В.
Методические предписания к выполнению контрольной работы по дисциплине «Теория оптимизации» предназначены для студентов заочной формы обучения направления подготовки 13.03.02 Электроэнергетика и электротехника. В методических предписаниях содержатся рекомендации по выполнению контрольной работы, требования к оформлению работы, рассмотрены теоретические основы с примерами решения аналогичных задач.
Методические предписания обсуждены и одобрены на заседании кафедры «Автоматизации, информационных и инженерных технологий» ЧФ ПНИПУ
«____»_____________20___ г., протокол №____.
И.о. зав. кафедрой, ст. преп. М.А. Шергина
Содержание
Цели и задачи 4
Порядок выполнения работы 4
Постановка задачи 4
Методические указания 4
Теоретические основы 5
Численные методы минимизации функций 5
1 Унимодальные функции 5
2 Выпуклые функции 6
3 Численные методы минимизации функции одной переменной 7
3.1 Метод перебора 7
3.2 Метод деления отрезка пополам 7
3.3 Метод золотого сечения 9
3.4 Метод касательных 10
3.5 Метод Ньютона 11
Варианты заданий на контрольную работу 13
Список рекомендуемой литературы 15
Цели и задачи
Контрольная работа по дисциплине «Теория оптимизации» выполняется в соответствии с Учебным планом для студентов заочной формы обучения направления подготовки 13.03.02 Электроэнергетика и электротехника.
Цель контрольной работы – закрепление и углубление знаний, полученных студентами в процессе изучения раздела «Основные понятия и определения. Методы безусловной минимизации функций» и темы «Классификация задач математического программирования» курса «Теория оптимизации», развитие навыков самостоятельной работы при решении конкретных задач с использованием методов минимизации функций
Порядок выполнения работы
Задание на контрольную работу является индивидуальным, выдается студенту лично во время установочной сессии. При работе над заданием студент может систематически получать консультации преподавателя. Выполненная контрольная работа с вложенным листом рецензии должна быть сдана в деканат не позднее, чем за месяц до начала следующей сессии.
Контрольная работа оформляется в отдельной тетради (12-18 листов) аккуратно, разборчивым почерком. Возможно оформление в печатном виде на листах формата А4 с титульным листом. В работе должны быть отражены все необходимые объяснения выполняемых действий, процесс решения и ответы.
Постановка задачи
Вариант контрольной работы состоит из двух частей. Первая часть включает ответы на два теоретических вопроса по темам: «Постановка задачи оптимизации» и «Классификация задач математического программирования».
Вторая часть включает в себя пять заданий по нахождению минимальных значений функций:
-
методом перебора;
-
методом деления отрезка пополам;
-
методом золотого сечения;
-
методом касательных;
-
методом Ньютона.
-
решение задачи симплексным и графическим методами.
Методические указания
Первая часть – ответы на теоретические вопросы:
Ответы на вопросы должны быть четкими, полными и аргументированными, при этом ответ на каждый вопрос должен занимать не более двух страниц печатного текста (шрифт Times New Roman №12 с междустрочным интервалом 1,5, параметры страницы (поля): верхнее – 2 см, нижнее – 2 см, левое – 3 см, правое – 1 см).
Вторая часть – «Численные методы минимизации функций»:
При выполнении контрольной работы необходимо привести все промежуточные вычисления в виде таблиц. Рекомендуется выполнение заданий в электронных таблицах MS Excel, что значительно облегчает вычисления. В этом случае необходимо вложить в контрольную работу скриншоты или переписать решение в тетрадь.
При решении четвертого задания (метод касательных) необходимо проверить функцию на выпуклость.
При решении задачи методом Ньютона значение х0 рекомендуется найти методом перебора на интервале [-10; 10] с шагом 1.
В методах с использованием производных (метод касательных и метод Ньютона) нахождение производных необходимо расписать.
Теоретические основы
Численные методы минимизации функций
1 Унимодальные функции
Число
![]() или
или
![]() есть локальный
минимум,
если
есть локальный
минимум,
если
![]() в некоторой -окрестности
точки
в некоторой -окрестности
точки
![]() .
.
Число
![]() называется точкой
глобального
(абсолютного)
минимума, если
называется точкой
глобального
(абсолютного)
минимума, если
![]() ,
,
![]() глобальный
минимум
(рисунок 1).
глобальный
минимум
(рисунок 1).
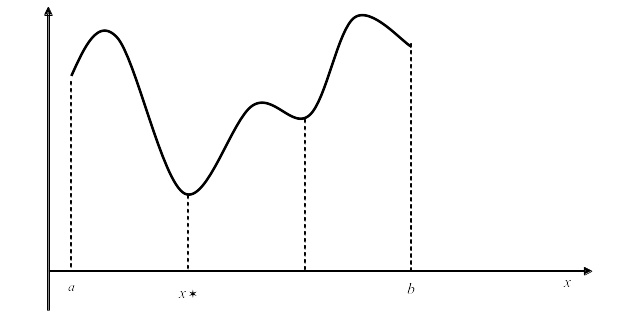
Рисунок 1
Под минимизацией
![]() на множестве U
будем понимать решение задачи найти
хотя бы одну точку минимума
на множестве U
будем понимать решение задачи найти
хотя бы одну точку минимума
![]() и
и
![]() этой функции на
U.
Такое решение называется оптимальным
или глобальным
минимумом.
этой функции на
U.
Такое решение называется оптимальным
или глобальным
минимумом.
Всякая точка глобального оптимума является точкой локального оптимума, обратное же неверно.
Многие приближенные методы минимизации применимы только тогда, когда любой локальный минимум является и глобальным. Один из классов функций, удовлетворяющих этому условию, составляют унимодальные функции.
Унимодальная функция обладает свойством, что она имеет единственный локальный минимум, но не обязана быть дифференцируемой и даже непрерывной.
Множество функций, унимодальных на отрезке a,b, будем обозначать Q[a; b].
Для
проверки унимодальности
![]() используют
следующий
критерий:
если
используют
следующий
критерий:
если
![]() дважды дифференцируема на
дважды дифференцируема на
![]() и
и
![]() то
то
![]() ,
т.е. унимодальна.
,
т.е. унимодальна.
Если вычислить значения унимодальной функции в четырех точках a, b, c, d интервала a; d, то всегда существует подинтервал, который не содержит оптимума и может, таким образом, быть удалён. Получаем уменьшенный интервал, на котором эту операцию можно повторить (рисунок 2).
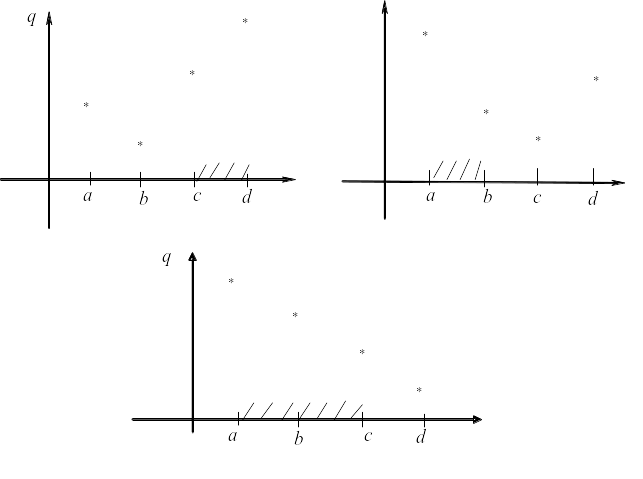
Рисунок 2
2 Выпуклые функции
Множество
![]() называется выпуклым,
если вместе
с любыми двумя точками x(1)
и x(2),
принадлежащими U,
оно содержит
отрезок, соединяющий эти точки.
называется выпуклым,
если вместе
с любыми двумя точками x(1)
и x(2),
принадлежащими U,
оно содержит
отрезок, соединяющий эти точки.
Пример.
![]() выпуклое
множество (рисунок 3).
выпуклое
множество (рисунок 3).
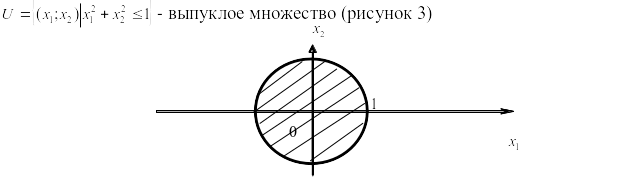
Рисунок 3
Если f (x) дважды дифференцируема на выпуклом множестве U и матрица её вторых производных положительно определена при всех xU, то f (x) является выпуклой на U.
Замечание.![]() Для
выпуклых функций всякий локальный
минимум является одновременно и
глобальным.
Для
выпуклых функций всякий локальный
минимум является одновременно и
глобальным.
3 Численные методы минимизации функции одной переменной
3.1 Метод перебора
Метод
перебора
является простейшим из прямых методов
минимизации. Пусть
![]() и требуется найти точку x*
на
и требуется найти точку x*
на
![]() с абсолютной погрешностью ,
в которой функция f(x)
принимает минимальное значение.
с абсолютной погрешностью ,
в которой функция f(x)
принимает минимальное значение.
Разобьём
![]() на
на
![]() равных частей точками деления
равных частей точками деления
![]() n
n
![]() .
.
Вычислим
значения
![]() в этих точках и путём сравнения найдём
в этих точках и путём сравнения найдём
![]() ,
в которой
,
в которой
![]() .
Тогда
.
Тогда
![]() .
.
Пример.
Найти минимальное
значение функции
![]() на отрезке
[1,5; 2] с
заданной точностью
= 0,05.
на отрезке
[1,5; 2] с
заданной точностью
= 0,05.
Решение:
![]()
|
|
1,50 |
1,55 |
1,60 |
1,65 |
1,70 |
1,75 |
1,80 |
1,85 |
1,90 |
1,95 |
2,0 |
|
|
-89,4 |
-90,2 |
-91,2 |
-91,8 |
-92,08 |
-92,12 |
-91,9 |
-91,4 |
-90,5 |
-89,4 |
-88 |
Ответ:
![]() .
.
3.2 Метод деления отрезка пополам
Метод деления
отрезка пополам
(дихотомии)
позволяет для любой функции
![]() построить последовательность вложенных
отрезков
построить последовательность вложенных
отрезков
![]() ,
каждый из которых содержит точку
,
каждый из которых содержит точку
![]() .
.
Пусть
>0
требуемая
точность определения
![]() .
Выбрав
2,
построим
последовательность
.
Выбрав
2,
построим
последовательность
![]() …,
используя рекуррентные формулы (рис.
6):
…,
используя рекуррентные формулы (рис.
6):
![]() .
.
При этом вычисляем
точность на каждом шаге
![]() .
Как только n<,
выписывают ответ:
.
Как только n<,
выписывают ответ:
![]() ,
f*=f(x*).
,
f*=f(x*).
Используя значения
функции в точках
![]() и
и
![]() ,
можно уменьшить рассматриваемый интервал
(рисунок 4).
,
можно уменьшить рассматриваемый интервал
(рисунок 4).
а)
если
![]() ,
то
,
то
![]() ,
,

б)
если
![]() ,
то
,
то
![]() ,
,
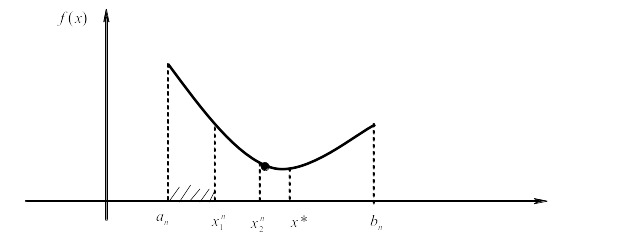
Рисунок 4.
Пример.
![]() = 0,05. Найти:
= 0,05. Найти:
![]() .
.
Решение. Пусть
![]()
|
n |
|
|
n |
|
|
|
|
Примечание |
|
0 |
1,5 |
2 |
0,25 |
1,74 |
1,76 |
-92,135 |
-92,096 |
|
|
1 |
1,5 |
1,76 |
0,13 |
1,62 |
1,64 |
-91,486 |
-91,696 |
|
|
2 |
1,62 |
1,76 |
0,07 |
1,68 |
1,70 |
-91,995 |
-92,084 |
|
|
3 |
1,68 |
1,76 |
0,04 |
- |
- |
- |
- |
|
![]() .
.
Ответ:
![]() .
.
3.3 Метод золотого сечения
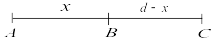 Золотым
сечением
отрезка
Золотым
сечением
отрезка
![]() называется
деление его на две неравные части так,
что отношение длины всего отрезка к
длине большей его части равно отношению
длины большей части к длине меньшей
части.
называется
деление его на две неравные части так,
что отношение длины всего отрезка к
длине большей его части равно отношению
длины большей части к длине меньшей
части.
![]() ,
,
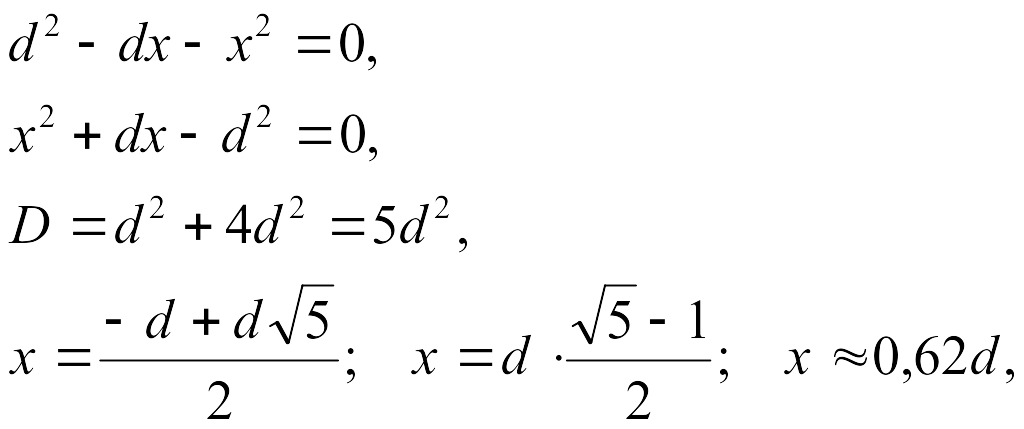
т.е.
![]() .
.

![]()
![]()
![]()
![]()
Пусть дан отрезок
![]() .
Найдём координаты точек золотого
сечения
.
Найдём координаты точек золотого
сечения
![]() и
и
![]() ;
d = b – a;
;
d = b – a;
![]()
Заметим, что x1 – a = b – x2 , откуда x1 = a + b – x2.
Пусть
![]() требуется найти
требуется найти
![]() ,
в которой функция f(x)
имеет минимум. Построим последовательность
,
в которой функция f(x)
имеет минимум. Построим последовательность
![]() и
и
![]() ,
следующим образом:
,
следующим образом:
-
если
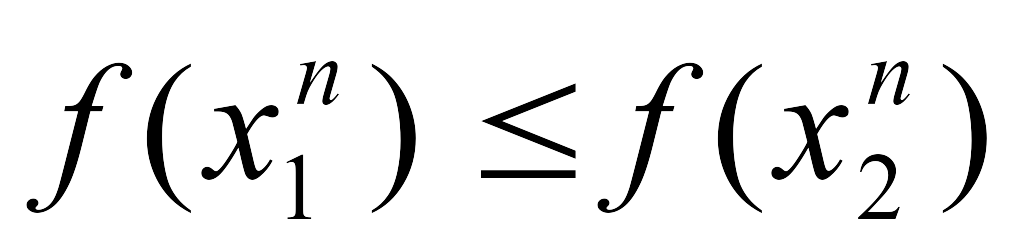 ,
то
,
то
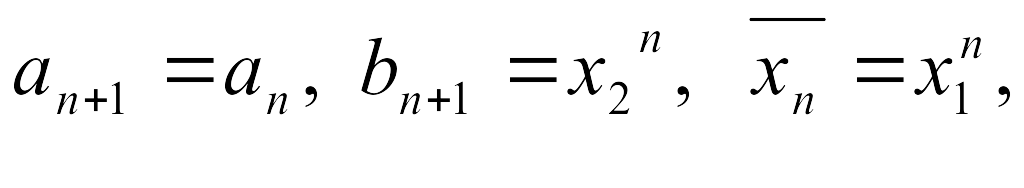
-
если
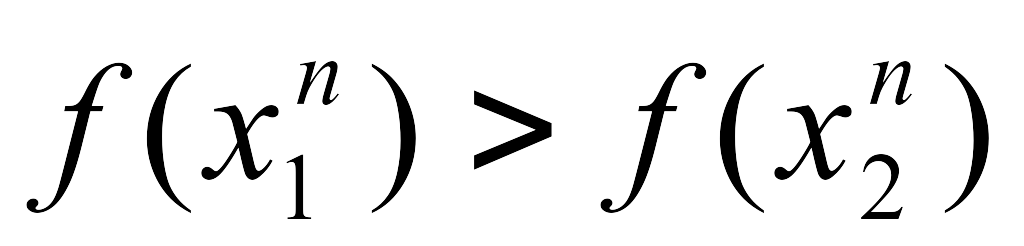 ,
то
,
то
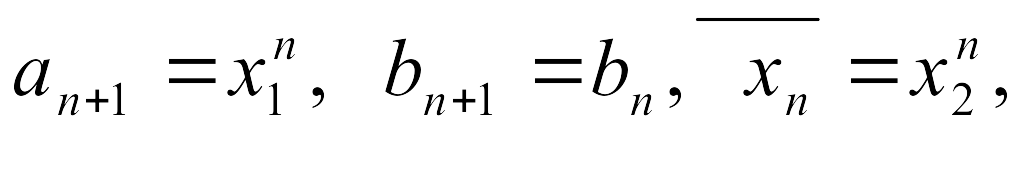
![]() где
где
![]() и
и
![]() –
первая и вторая точки золотого сечения
на
–
первая и вторая точки золотого сечения
на
![]() .
.
Вместо того, чтобы вычислять n на каждом шаге, удобнее вычислить число шагов, при этом на последнем шаге точность будет достигнута.
Выразим n через :
![]() .
.
Пример.
![]() ,
= 0,05.
,
= 0,05.
Решение. Вычислим
![]() т.е.
т.е.
![]() .
Т.о. точность
будет достигнута на пятом шаге.
.
Т.о. точность
будет достигнута на пятом шаге.
|
n |
|
|
|
|
|
|
Примечание |
|
1 |
1,5 |
2 |
1,691 |
1,809 |
-92,049 |
-91,814 |
|
|
2 |
1,5 |
1,809 |
1,618 |
1,691 |
-91,464 |
-92,049 |
|
|
3 |
1,618 |
1,809 |
1,691 |
1,736 |
-92,049 |
-92,138 |
|
|
4 |
1,691 |
1,809 |
1,736 |
1,764 |
-92,138 |
-92,083 |
|
|
5 |
1,691 |
1,764 |
1,719 |
1,736 |
-92,109 |
-92,138 |
|
Ответ:
![]() .
.
3.4 Метод касательных
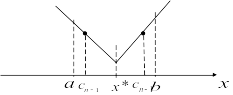 Для
нахождения минимума f(x)
рассматриваем функции, выпуклые вниз
на
Для
нахождения минимума f(x)
рассматриваем функции, выпуклые вниз
на
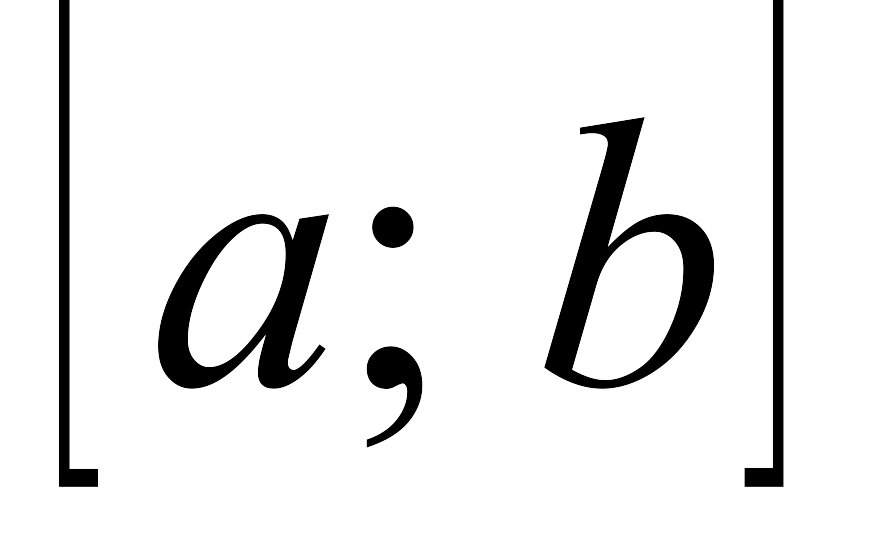 ,
а для этого необходимо, чтобы
,
а для этого необходимо, чтобы
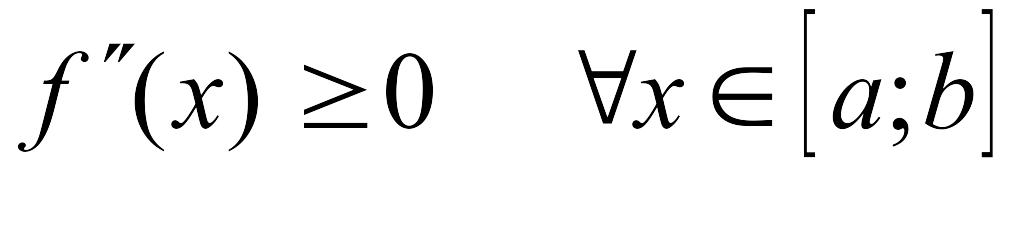 ,
причём
,
причём
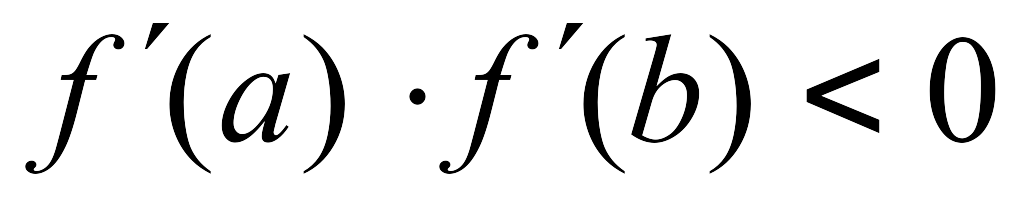 (рис. 5).
(рис. 5).
Рисунок 5.
Если
![]() то
то
![]() .
.
Если
![]() то
то
![]() .
.
Отсюда, алгоритм
нахождения
![]() .
Построим
последовательности
.
Построим
последовательности
![]() в соответствии с рекуррентными формулами:
в соответствии с рекуррентными формулами:
![]() ,
,
![]() при
при
![]() ,
,
![]() при
при
![]() .
.
Требуемая точность
минимизации считается достигнутой,
если
![]() т.е.
т.е.
![]() .
Выписываем
решение
.
Выписываем
решение![]() .
.
Пример.
Доказать, что
![]() выпукла на
выпукла на
![]() ,
и минимизировать её методом касательных
с точностью
=0,05.
,
и минимизировать её методом касательных
с точностью
=0,05.
Решение:
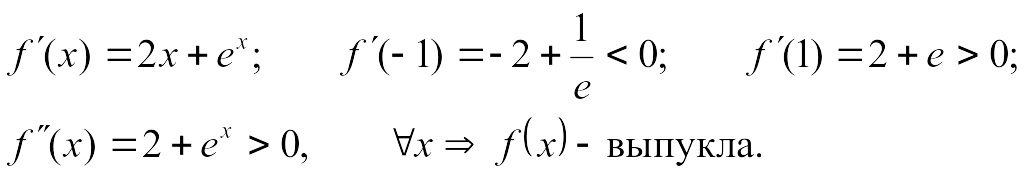
![]() ;
;
|
|
|
|
|
|
Примечание |
|
0 |
-1 |
1 |
0,11620 |
1,356 |
|
|
1 |
-1 |
0,11620 |
-0,41637 |
-0,173 |
|
|
2 |
-0,41637 |
0,11620 |
-0,14313 |
0,58 |
|
|
3 |
-0,41637 |
-0,14313 |
-0,27806 |
0,02 |
|
Ответ:
![]() .
.
Замечания: а)
при
![]() ;
;
б)
при
![]() ;
;
в)
при
![]()
при
![]() .
.
3.5 Метод Ньютона
Этот метод
обеспечивает более высокую скорость
сходимости к
![]() .
.
Пусть
![]()
выпуклая, дважды дифференцируемая
функция. Выбрав начальное приближение
выпуклая, дважды дифференцируемая
функция. Выбрав начальное приближение
![]() ,
построим последовательность
,
построим последовательность
![]()
При
![]()
получим
ответ
получим
ответ
![]() .
.
Пример.
![]() где
=10-7.
По области определения
где
=10-7.
По области определения
![]() .
.
Пусть
![]() ,
проведем вычисления по формуле
,
проведем вычисления по формуле
![]() :
:
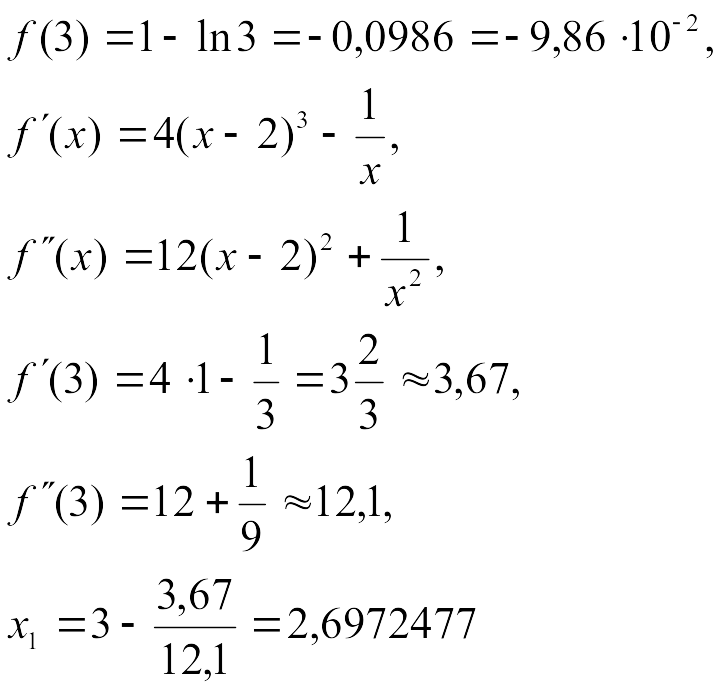
и т. д.
Заполним таблицу:
|
|
|
|
|
|
0 |
3 |
-0,0986 |
3,67 |
|
1 |
2,6972477 |
-0,7558859 |
0,985 |
|
2 |
2,5322701 |
-0,8488508 |
0,208 |
|
3 |
2,4736906 |
-0,8553636 |
|
|
4 |
2,4663735 |
-0,8554408 |
|
|
5 |
2,4662656 |
-0,8554408 |
|
Ответ:
![]() .
.
Замечания:
1. При неудачном
выборе
![]() последовательность
последовательность
![]() n = 1, 2,…,
может расходиться. Если же
n = 1, 2,…,
может расходиться. Если же
![]() достаточно близко к
достаточно близко к
![]() ,
то последовательность
,
то последовательность
![]() ,
сходится быстро.
,
сходится быстро.
2. Метод Ньютона
часто используется на завершающем этапе
минимизации, когда точка минимума x*
грубо найдена другим, менее трудоёмким,
методом и требуется найти
![]() с большей точностью.
с большей точностью.