ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.05.2019
Просмотров: 496
Скачиваний: 1
11
В
ари
ан
т
Состав ветвей схемы
1
2
3
4
5
6
7
8
9
10 11
12
13
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
R/Е,
17 8/80
2
0
4
∞ ∞ 2/10 0
6
∞ 0
0
6
18
0
0
10/8
∞ 4
∞ 0
2
∞
4 4/60 0 2/16
19 2/40
0
2/8 4/10 0
∞ ∞ ∞
2
8
2
4
8
20 4/60 2/15
0
2
∞ ∞ 4
0
6
∞ 0
2
0
Задача №2. Применение средств CAE при анализе стационарных
и динамических режимов линейных электрических цепей переменного
тока
Цепь переменного тока подключена к источнику входного напряже-
ния. Варианты заданий приведены в таблице 2. По результатам выполне-
ния задания составить отчет на листах А4 и в электронной форме.
Содержание задания:
1) принять за варьируемую величину С, L, f и построить зависимо-
сти Р, Q, S, cosφ
вх
, φ
вх
, I
вх
(C, L, f) и оценить полученные результаты по ре-
жимам работы, характеру двухполюсника, энергетическим показателям;
2) если в схеме есть две индуктивности исследовать влияние взаимо-
индукции при согласном (встречном) включении и Ксв = 0…1, предложить
варианты уменьшения взаимоиндуктивного влияния;
3) провести динамическое исследование переходного процесса под-
ключения (отключения) схемы к предлагаемому источнику напряжения,
сделать выводы исходя из сравнения с токами и напряжениями устано-
вившегося режима, предложить варианты оптимизации (автоматическая
система включения при фазе равной 0, дополнительные элементы в схеме),
подтвердить эффективность оптимизации.
Пояснения
пункт выполнять в MathCAD
проверку провести в программе Multisim для п.п. 1 (по одной точ-
ке для каждого графика проверить), 2 (для одного значения К
св
при со-
гласном (встречном) включении проверить), 3 (привести осциллограмму
или график).
Примеры листингов и методические рекомендации
1. Исследования зависимостей Р, Q, S, cosφ
вх
, φ
вх
, I
вх
(C, L, f)
12
Для исследования зависимостей Р, Q, S, cosφ
вх
, φ
вх
, I
вх
(C, L, f) можно
воспользоваться методикой применения варьируемых (ранжированных)
переменных (см. практическое занятие 2).
2. Исследование влияния взаимоиндукции
При исследовании влияния взаимоиндукции использовать либо ком-
плексную форму, либо мгновенные значения.
Взаимоиндуктивное сопротивление:
M
X
M
;
– взаимная индуктивность:
2
1
L
L
K
M
ñâ
;
– взаимоиндуктивные напряжения влияния первой индуктивности на
вторую и второй на первую:
12
2
12
M
M
jX
I
U
,
21
1
21
M
M
jX
I
U
;
– для дуальных цепей:
21
12
M
M
M
X
X
X
;
– полное напряжение на индуктивности с учетом самоиндукции и
взаимоиндукции для двух катушек L
1
и L
2
:
M
L
L
jX
I
jX
I
U
2
1
1
1
,
M
L
L
jX
I
jX
I
U
1
2
2
2
(при согласном включении ка-
тушек знаки у напряжений самоиндукции и взаимоиндукции одинаковы).
Влияние взаимоиндукции можно исследовать вместе с п. 1, введя со-
ответствующие выражения в мат. модель.
3. Исследование переходных процессов
При динамическом исследовании переходного процесса подключе-
ния (отключения) схемы к предлагаемому источнику напряжения можно
применять как численные, так и аналитические методы. Оба направления
опираются на интегро-дифференциальные уравнения для послекомутаци-
онной цепи, составленные, например, по законам Кирхгофа. Дифференци-
альная (интегральная) форма напряжений и токов на R, L, C элементах:
R
i
u
R
,
dt
di
L
u
L
,
idt
C
u
C
1
,
R
u
i
R
,
udt
L
i
L
1
,
dt
du
C
i
C
.
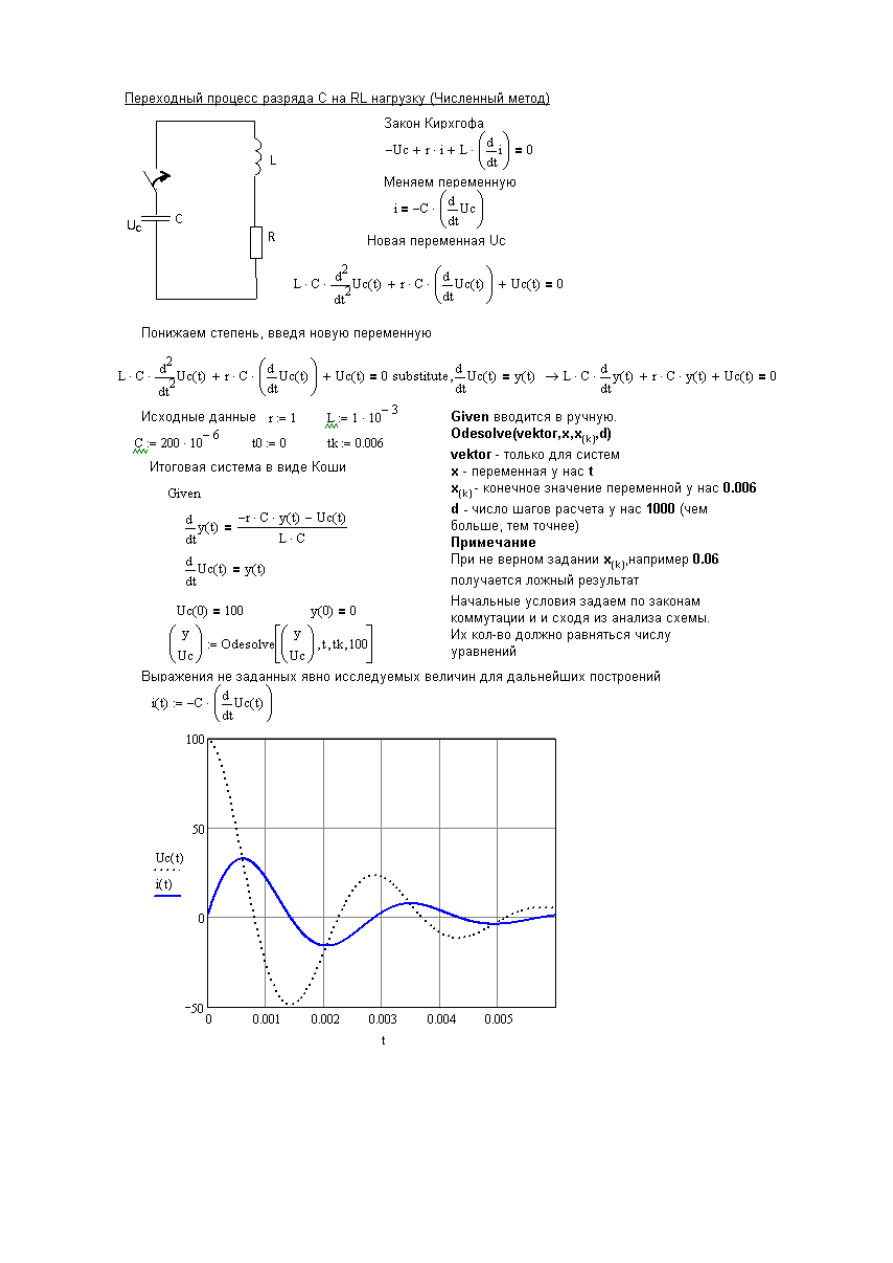
Методика численного решения предполагает преобразование исход-
ной системы (мат. модели) для послекомутационной схемы к системе
дифференциальных уравнений первого порядка в виде Коши (см. листинг
MathCAD).
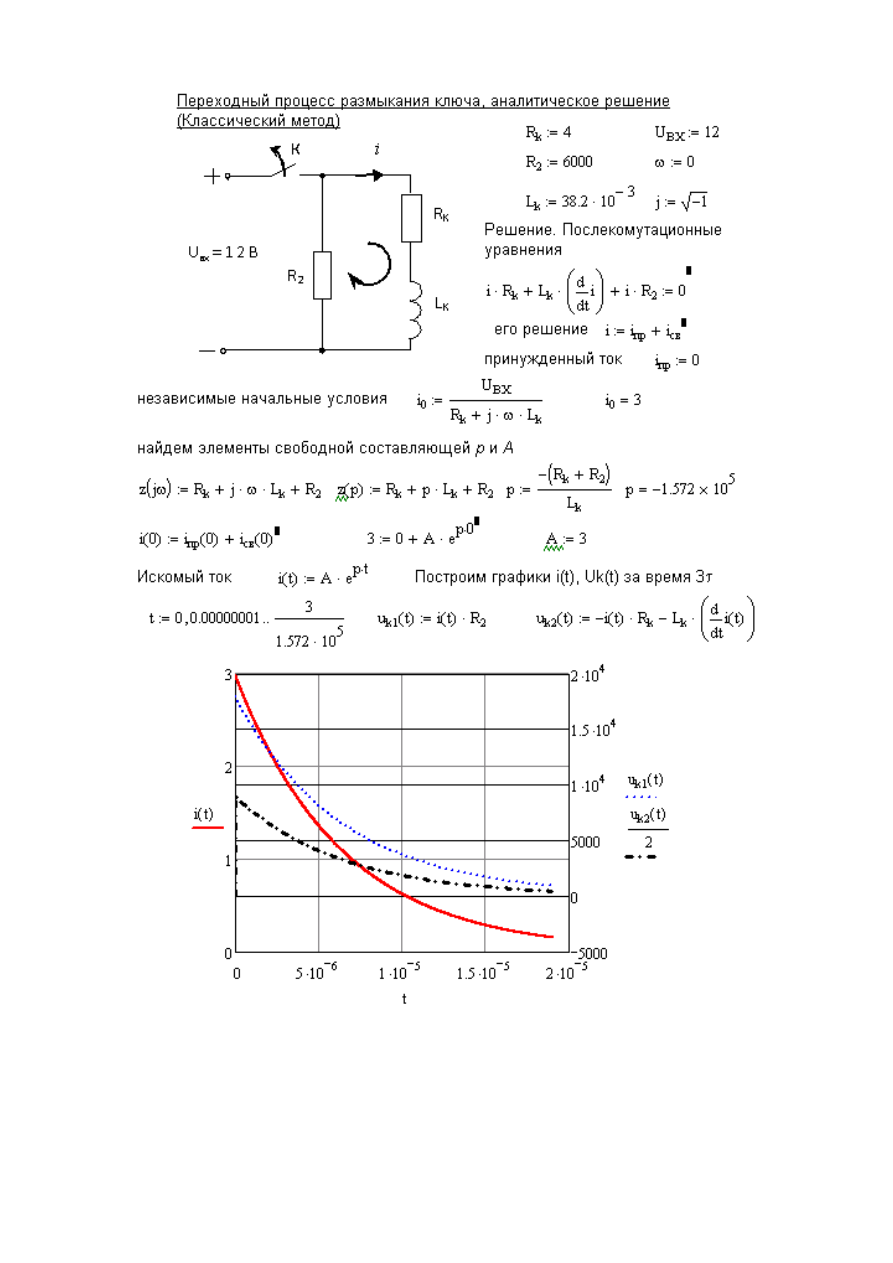
Методика аналитического решения (классический метод, оператор-
ный метод и др.), предполагает предварительное выполнение ряда анали-
тических
преобразований
и
получение
результатов
в
виде
функциональных зависимостей i(t), u(t). Пример применения классическо-
го метода расчета переходных процессов приведен далее.
13
14
15
Варианты заданий для самостоятельного решения
Рекомендуется применить методику расчета электрической цепи с
одним источником ЭДС путем эквивалентного преобразования схемы.
На рисунке 2 приведен скелет расчетной электрической цепи, со-
держащей до девяти потребителей, а в таблице 2 указаны исходные дан-
ные.
Для всех вариантов ω = 314 рад/с, r
1
= 3 Ом, r
2
= 7 Ом, r
3
= 10 Ом,
L
1
= 15,92 мГн,
L
2
= 25,48 мГн,
L
3
= 38,22 мГн,
С
1
= 796,2 мкФ,
С
2
= 398,1 мкФ, С
3
= 318,5 мкФ.
Т а б л и ц а 2
Вариант
Um,
В
φ
o
,
град.
1 2 3 4 5 6 7 8 9
1
380
0
r
1
L
1
- r
2
L
2
С
2
r
3
L
3
-
2
127 30 r
1
- - r
2
L
2
- r
3
L
3
С
2
3
36
60
- L
1
- r
2
- С
2
r
3
L
3
-
4
220 90 L
3
С
1
- r
1
- - r
2
-
5
60 120 r
1
L
1
С
1
L
2
- - С
3
- -
6
100 45 r
2
L
2
- r
1
L
1
С
1
r
3
L
3
-
7
70
0
r
3
- С
3
r
1
L
1
С
1
- L
2
С
2
8
120 -30 r
1
L
1
- r
2
- С
2
r
3
L
3
С
3
9
90
-60 r
2
- С
2
r
1
- С
1
r
3
L
3
-
10
380 -90 - L
1
С
1
r
2
- С
2
r
3
L
3
-
11
150
0
r
1
- С
1
r
2
- С
2
r
3
L
3
С
3
12
160 30
- L
1
- r
2
L
2
С
2
r
3
- С
3
1
3
Рисунок – 2
2
u
=
U
m
si
n(ω
t+φ
o
)
4
5
6
7
8
9