Добавлен: 23.10.2018
Просмотров: 1886
Скачиваний: 24

ПРОГРАММИРОВАНИЕ МАТРИЧНЫХ ОПЕРАЦИЙ
Выбрать задание по последним двум цифрам своего студенческого билета.
1) Рассчитать элементы квадратной матрицы A = (a
ij
), i,j = 1,2,...,n по
заданной формуле.
2) Вычислить элементы вектора-столбца X = (x
i
), i = 1,2,...,n по заданному
правилу (см. справку по функциям Excel).
3) Выполнить требуемое упорядочение элементов матрицы А или вектора Х.
Для этого:
скопировать значения матрицы А или вектора Х и вставить на свободное
место с помощью команды Правка Специальная вставка…
значения
.
Затем выделить нужную область для сортировки и выполнить команду
Данные
Сортировка…. В появившемся диалоговом окне отметить
пункт
сортировать в пределах указанного
и нажать кнопку
«Сортировка…» Затем в следующем диалоговом окне пометить, как надо
сортировать – по возрастанию или убыванию и нажать «ОК».
4) Вычислить значение скалярной величины y по заданной формуле.
5) Вычислить вектор В – произведение матрицы А на столбец Х с помощью
функции МУМНОЖ.
Размерность задачи n назначается преподавателем.
Пример оформления:
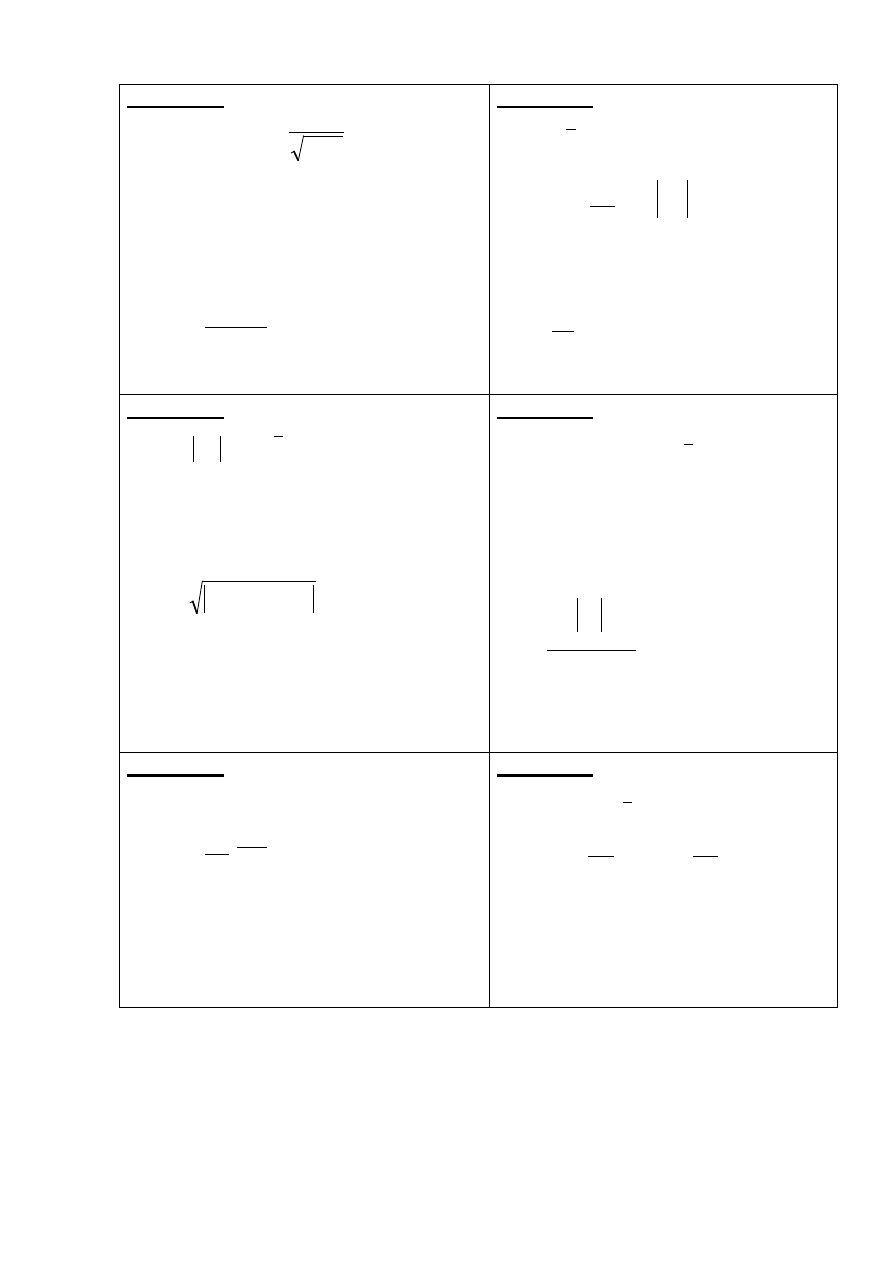
Вариант 1
1)
;
j
i
)
i
(
j
i,
a
j
2
2
2
4
1
2
,
,
2)
n
1
j
;
j
i,
a
ij
a
i
n
x
3) упорядочить
нечетные
по
номеру
элементы вектора
Х
по убыванию
абсолютных значений;
4)
n
i
.
i
n
x
i
x
y
1
1
Вариант 2
1)
j);
ln(i
j
i
ji
a
2)
;
)
ji
a
ij
(a
n
1,
j
max
i
x
3) упорядочить
элементы
главной
диагонали матрицы
А
по возрастанию
значений;
.
1
n
1
j
j
ji
x
y
Вариант 3
1)
);
j
(i
j
i
j
i,
a
2
1
2
2)
x
i
– скалярное произведение
i
-ой
строки на главную диагональ;
3) упорядочить элементы последних трех
строк
матрицы
А
по возрастанию
значений;
4)
.
n
x
...
2
x
1
x
y
Вариант 4
1)
;
j
i
5
ln
j)
sin(i
ji
a
2)
x
i
– скалярное произведение
первой строки на
i
-ый столбец;
3) упорядочить
элементы
четных
столбцов матрицы
А
по возрастанию
абсолютных значений;
4)
.
i
x
i
x
y
0
i
x
n
1
i
0
x
n
1
i
Вариант 5
1)
;
j
i
tg
1
n
j
i,
a
2)
;
)
i!
ji
a
(
n
1,
j
min
i
x
3) упорядочить элементы последнего столбца
матрицы
А
по возрастанию значений;
4)
n
1
i
.
1
j
-
n
x
j
x
y
Вариант 6
1)
;
j
i
2)
(i
ji
a
2)
);
ji
(a
n
1,
j
min
)
ij
(a
n
1,
j
max
i
x
3)упорядочить элементы вектора
Х по убыванию значений;
4)
.
n
1
j
)
1
i
-
n
n
j
(x
y

Вариант 7
1)
;
1)
j
6
2
j
(2
i
2
2
i
5,5
j
i,
a
2)
x
i
– вторая строка матрицы, полученная
делением матрицы
А
на максимальный
элемент матрицы
А
;
3) упорядочить элементы первого столбца
матрицы
А
по возрастанию значений;
4)
.
1
n
1
i
1
i
x
1
i
x
1
Вариант 8
1)
;
5
j)
ln(i
10
1
i
8,4
j
2,2
ji
a
2)
n
1
j
)
ij
ln(b
i
x
, где
b
ij
–элементы
матрицы, полученной заменой
a
ii
на
сумму элементов
i
-й строки;
3) упорядочить элементы строк матрицы
А
по убыванию значений;
4)
.
1
n
2
i
1
i
x
i
x
i
x
1
i
x
y
Вариант 9
1)
;
j
j)
sin(n
)
cos(i!
j
i,
a
2)
n
1,
k
ki
a
max
ij
a
n
1,
j
max
i
x
;
3)упорядочить элементы последнего столбца
матрицы
А
по возрастанию значений;
4)
.
3
n
x
...
2
x
1
x
y
Вариант 10
1)
;
i
2
j
)
ln(i!
ji
a
2)
х
i
– скалярное произведение
i
-й
строки на побочную диагональ;
3) упорядочить элементы последних трех
столбцов матрицы
А
по возрастанию
значений;
4)
.
n
1
i
n
i
x
x
,
n
1
i
1
n
2
x
i
x
y

Вариант 11
1)
;
3
5
j
i
2
j)
3
i
(2
j
i,
a
2)
0
ij
a
;
)
ij
a
(
n
1,
j
max
i
x
3) упорядочить элементы вектора
Х
по возра
станию абсолютных значений;
4)
.
..
7
x
5
x
5
x
3
x
3
x
1
x
y
Вариант 12
1)
;
j
1,2
i
7
i
2
3!
i
j
ji
a
2)
;
n
1
j
)
1
i
-
n
j,
cos(a
ij
a
i
x
,
3) упорядочить
элементы
последнего
столбца матрицы
А
по возрастанию
значений;
4)
1
n
x
)
n
x
1
n
x
2
n
(x
...
3
x
)
4
x
3
x
2
(x
2
x
3
x
2
x
1
x
y
Вариант 13
1)
;
i
2)
(
j
3
2
1
j
i,
a
2)
n
1
j
);
i
1,
j
n
a
ij
sin(a
i
x
3) упорядочить элементы первых трех строк
матрицы А по возрастанию значений;
4)
.
)
i
(x
n
1,
i
min
)
i
(x
n
1,
i
max
y
Вариант 14
1)
;
j
/e
i
e
2
/j
j
2
2
/i
i
2
ji
a
2)
n
1
j
),
ij
sin(b
i
x
где b
ij
– элементы
матрицы,
полученной
заменой
элементов
побочной
диагонали
матрицы
А
суммой
элементов
соответствующего столбца;
3) упорядочить
элементы
нечетных
столбцов матрицы А по возрастанию
значений;
4)
.
1
-
n
1
i
n
1
i
x
y
Вариант 15
1)
;
!
j
i!
j
i,
a
2)
n
1
j
ik
a
n
1,
k
max
ij
a
i
x
3) упорядочить элементы побочной диагона
ли матрицы А по возрастанию значений;
4)
.
1
n
1
i
1
i
x
1
i
x
1
Вариант 16
4)
;
1)
ln(j
1)
ln(i
i)
ln(j
ji
a
5)
x
i
–
скалярное произведение i-й строки
на
i-
й столбец;
6) упорядочить нечетные по номеру
элементы вектора
Х
по возрастанию
значений;
i
x
n
1,
i
min
)
i
(x
n
1,
i
max
y
4)
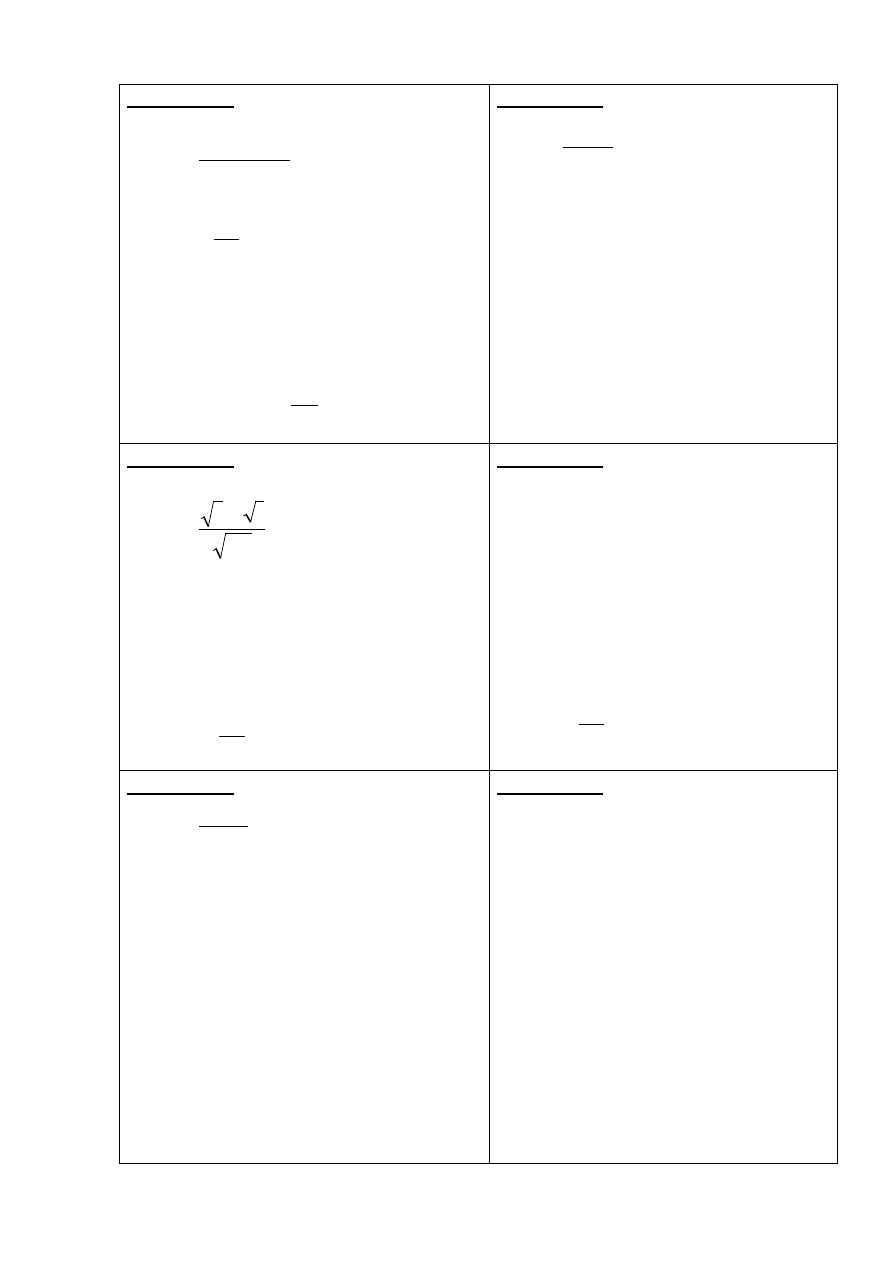
Вариант 17
1)
1)
j
lg(i
n
j
1
-
i
j
i,
a
2)
n
1
k
)
kj
a
ij
a(
n
1,
j
min
i
x
;
3) упорядочить элементы последней строки
матрицы А по убыванию значений;
4)
.
n
1
i
i
n
1
i
1
i
n
y
i!
x
x
Вариант 18
1)
;
j
i
i
j
j
i
ji
a
5)
х
i
– скалярное произведение
i
-й строки
на
i-
й столбец матрицы,
полученной
из исходной заменой диагональных
элементов
на
сумму
элементов
соответствующей строки;
6) упорядочить элементы четных строк
матрицы А по убыванию значений;
7)
.
x
n
1
i
1
i
-
n
n
1
i
i
x
y
Вариант 19
1)
j
i
i
j
j
i,
a
j
i
;
2)
x
i
– среднеарифметическое значение
положительных элементов
i-
й строки;
3)
упорядочить
элементы
побочной
диагонали
матрицы
А
по
убыванию
абсолютных
значений;
4)
).
ii
/a
i
(x
n
1,
i
max
y
Вариант 20
7)
;
j)
lg(i
j)
i
5
(
ji
a
8)
x
i
–
среднеарифметическое значение
отрицательных элементов
i-
го столбца;
9) упорядочить элементы первых трех
столбцов матрицы А по возрастанию
значений;
)
1
i
n
i,
/a
i
(x
n
1,
i
min
y
4)
Вариант 21
1)
3
j)
(i
j
i,
a
j!
i!
2)
)
ji
n
1
j
cos
n
1
j
ij
a
i
x
(a
10) упорядочить элементы первых трех столб
цов матрицы А по убыванию абсолют
ных значений;
4)
0
i
x
n
1
i
).
i!
i
tg(x
y
Вариант 22
1)
j);
5
i
sin(2
ji
a
2)
;
)
ji
cos(a
i
1
i
n
1
i
ji
a
x
i
3) упорядочить элементы четных строк
матрицы А по убыванию значений;
4)
i
1
n
n
2,4...
i
i
y
x
x