Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых

Кафедра ВТ и СУ

Практическая работа

по дисциплине «Компьютерные системы поддержки принятия решений»

«Многокритериальный альтернативный выбор с использованием

нечетких оценок критериального соответствия»

Владимир 2018

Многокритериальный альтернативный выбор с использованием нечетких оценок критериального соответствия.

1. Основы теории.

Этот простейший случай предполагает, что каждая альтернатива содержит только однопродуктовую программу. Для решения задачи необходимо построить отношение между множествами Р и С:

R:PC или PRC, (1)

которое определяет, с какой степенью та или иная программа соответствует критериям C.

Здесь

– множество возможных продуктовых программ;

– множество критериев,

по которым осуществляется оценка продуктовых программ и альтернатив. В качестве таких критериев можно, например, рассматривать влияние на показатели оборота, размеры денежных потоков, а также капитала и имущества в будущих периодах, уровень риска, очевидно, могут использоваться и немонетарные показатели (критерии).

Поскольку речь идет о новых продуктах, то попытки точных расчетов вовсе не гарантируют, что их результаты будут реализованы.

Наиболее часто для решения данной задачи используется метод балльных оценок, когда отношение (1) задается матрицей

г де – числа в некоторой шкале.

Пример расчета по этой методике приведен в таблице1.

Таблица 1.

Факторы привлекательности рынка для мультифакторной модели бизнес-портфеля

Экономический критерий	Вес (0-1)	Продукт Р1		Продукт Р2		Продукт Р3
		Оценка (0-5)	Ценность= вес * оценка	Оценка (0-5)	Ценность= вес * оценка	Оценка (0-5)	Ценность= вес * оценка
Привлекательность рынка
С1 – общий объем рынка С2 – показатель темпов роста в год С3 – маржа прибыли С4 – интенсивность конкуренции С5 – технологические требования С6 – влияние инфляции С7 – энергоемкость С8 – воздействие окружающей среды С9 – социальный / политический/ юридический аспекты Итого Эффективность бизнеса С1 – доля рынка С2 – темпы роста доли рынка С3 – качество продукции С4 – репутация марки С5 – распределение продукции С6 – эффективность продвижения С7 – возможности производства С8 – эффективность производства С9 – расходы подразделения С10 – поставки материалов С11 – эффективность научных исследований С12– управленческий аппарат Итого	0,2 0,2 0,15 0,15 0,15 0,05 0,05 0,05 *** 1,0 0,1 0,15 0,1 0,1 0,05 0,05 0,05 0,05 0,15 0,05 0,1 0,05 1,0	4 5 4 2 3 4 2 3 27 4 2 4 5 4 3 3 2 3 5 3 4 42	0,8 1,0 0,6 0,3 0,6 0,15 0,1 0,15 3,7 0,4 0,3 0,4 0,5 0,2 0,15 0,15 0,1 0,45 0,25 0,3 0,2 3,4	3 4 3 4 4 5 4 4 31 4 3 5 4 3 4 2 3 2 4 4 3 41	0,6 0,8 0,6 0,6 0,6 0,25 0,2 0,2 3,7 0,4 0,45 0,5 0,4 0,15 0,2 0,1 0,15 0,3 0,2 0,4 0,15 3,4	4 4 4 3 3 4 2 1 24 3 4 4 4 4 3 3 2 3 3 4 2 39	0,8 0,8 0,6 0,45 0,45 0,45 0,1 0,05 3,7 0,3 0,6 0,4 0,4 0,2 0,15 0,15 0,1 0,45 0,15 0,4 0,1 3,4

---

Как следует из таблицы 1 все продукты как по привлекательности рынка, так и по эффективности бизнеса с учетом весов критериев получили одинаковые оценки. Это достаточно характерная ситуация для метода среднего балла, так как вычисление среднего создает эффект сглаживания. Кроме того, полученные результаты наглядно иллюстрируют влияние выбора весовых коэффициентов. Из таблицы 1 видно, что при отсутствии весовых коэффициентов альтернативы получили различные оценки и решение могло быть принято. Не следует исключать и ситуации, когда альтернативы получать одинаковые оценки по методу среднего балла и без учета весовых коэффициентов. Их произвольное введение в этом может просто исказить реальную ситуацию и привести к неправильному решению. Следует также отметить, что оценки, приведенные в таблице 1, вообще говоря, не следует рассматривать как точные, скорей всего они являются предполагаемыми, и в процессе реализации проекта они могут измениться.

Одним из вариантов преодоления указанных выше затруднений может быть использование в процессе выбора наилучшего решения переход к нечетким числовым оценкам.

Представим оценки и весовые коэффициенты из табл. 1 в виде нечетких чисел (рис. 1, 2).

Оценки

1

1 2 3 4 5 x

Рис. 1. Функции принадлежности нечетких оценок

1

0,05 0,10 0,15 0,20 0,25 0,3 0,35 0,4 0,45 0,5 х

Рис. 2. Функции принадлежности нечетких весовых

коэффициентов

Задание 1. Используя таблицу Fuzzi Calc провести расчет показателей привлекательности рынка и эффективности рынка для каждого альтернативного продукта.

Наилучшая альтернатива должна иметь наибольшие оценки как по привлекательности рынка, так и по эффективности бизнеса. Если этот результат не получен выполнить задание 2.

Задание 2. Если однозначное решение задачи не получено рассчитываются нечеткие матрицы уступок R^-1, R^-2, R^-3 для обеих оценок. Элементы этих матриц рассчитывают по формуле

_lk(х) = 1 – _j,r (х),

где i =1, 2, 3; jI,

k – определяется количеством критериев;

l =1,….n – 1, в нашем примере n = 3.

Наихудшей ситуацией для каждой альтернативы является минимум уступок со стороны других альтернатив. Этот минимум находится как операция пересечения элементов каждой строки матриц уступок, т. е. находим = min_lk^-i (x).

Наилучшая ситуация будет в случае максимальных уступок:

(x) = max(x).

Пример расчета приведен в таблице 2.

Таблица 2

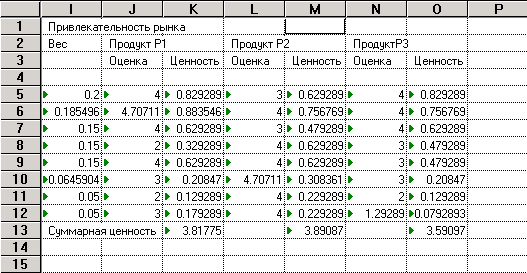
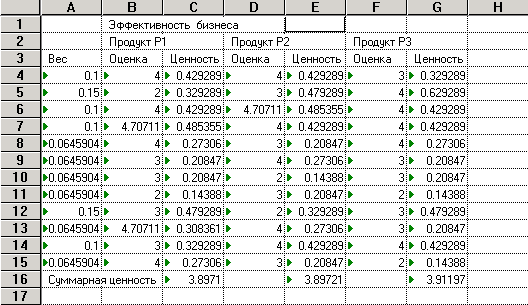
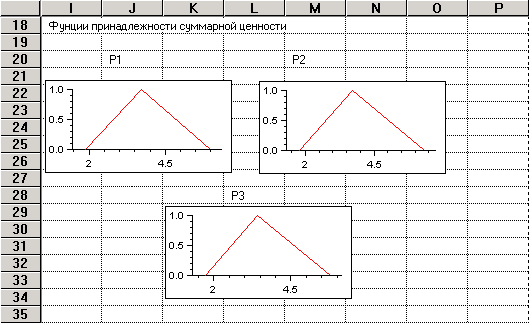
Рис. 3. Функции принадлежности оценок суммарной ценности

по критерию «Привлекательность рынка»

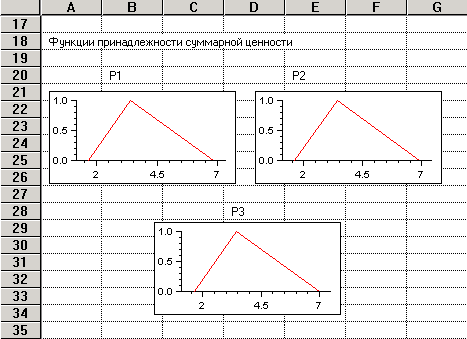
Рис. 4. Функции принадлежности нечеткой оценки суммарной ценности

по критерию «Эффективность бизнеса»

Соответствующие результаты обозначены MAX(MIN) в табл. 3. Функции принадлежности приведены на рис. 5, 6.

Таблица 3

    

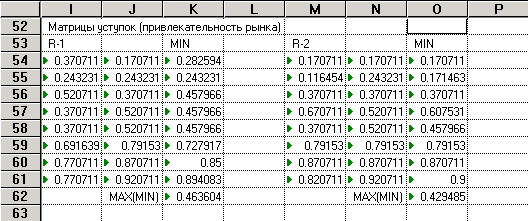
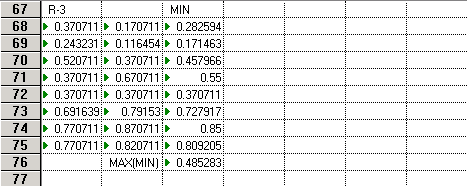
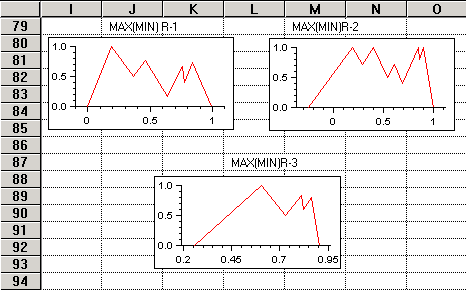
Рис. 5. Результирующие оценки критериев сравнения

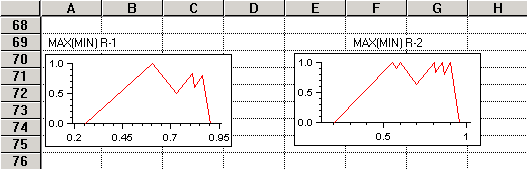
Рис. 6. Итоговые нечеткие оценки по критерию

---

«Эффективность бизнеса» на основе нечеткой матрицы уступок

Точечные оценки получаются по методу центра тяжести

MIN(MAX)=^’(x)*x/^’(x).

Здесь также имеет место неоднозначная ситуация:

по привлекательности рынка

P₁:MAX(MIN) = 0,463604;

P₂:MAX(MIN) = 0,429485;

P₃:MAX(MIN) = 0,485283.

по эффективности бизнеса

P₁:MAX(MIN) = 0,625115;

Р₂:MAX(MIN) = 0,638415;

P₃:MAX(MIN) = 0,485283

Если просуммировать все полученные оценки, то ситуация разрешается в пользу продукта Р₂

Р₁:8,803569, Р₂:8,85595, Р₃:8,392236.

Более убедительные результаты получаются, если для получения итоговых значений воспользоваться операцией пересечения оценок. Суммарные ценности по «эффективности бизнеса» и «привлекательности рынка» получаются в виде нечетких чисел с соответствующими функциями _эб, _пр, тогда итоговая оценка определяется как ₁= min_эб,_пр, аналогично определяется

₂ = minMAX(MIN)_эб,MAX(MIN)_пр (табл. 4, рис. 7).

Таблица 4

Аналогичные расчеты выполняются и для соответствующих матриц уступок μ_-j = min{[MAX(MIN)/R^-j_пр],[MAX(MIN)/R^-j_эф.б]},

j = 1,2, 3 (табл. 5, рис. 8).

Таблица 5

Минимум уступок

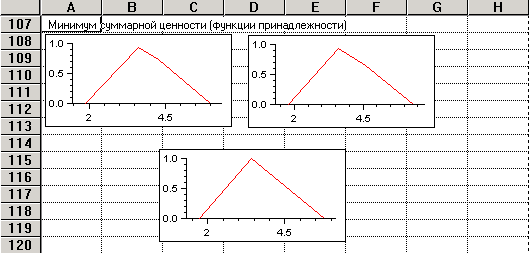
Рис. 7. Функции принадлежности нечетких оценок суммарной ценности

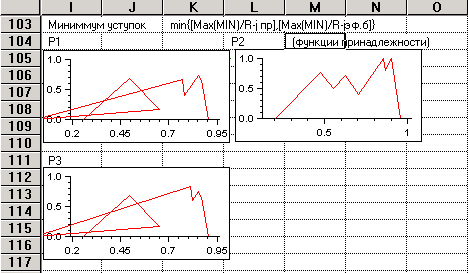
При таком подходе продукт Р₂ однозначно получает достаточно заметное преимущество. Окончательное решение может быть получено, если вычислить сумму (рис. 8).

Рис. 8. Функция принадлежности итоговой суммарной оценки по проектам

Задание по выполнению лабораторной работы.

1. Используя рассмотренный пример, провести выбор наилучшей альтернативной продуктовой программы.

2. Сформулировать собственный пример и провести соответствующие расчеты.

3. Проанализировать полученные результаты.

Содержание отчета.

1. Результаты исследований.

2. Выводы.

---

Смотрите также файлы

• Математическая логика и конечные автоматы МУ к курсовой.doc

• Технологии программирования.docx

• Лабораторная 2.doc

• Основы инфокоммуникационны технологий.pdf

• Задание для теоретической части курсовой работы.pdf