ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 25.10.2018
Просмотров: 10339
Скачиваний: 105

81
– действия с пером: процедуры и функции;
– действия с кистью: процедуры и функции;
– стили штриховки кисти;
– действия со шрифтом: процедуры и функции;
– стили шрифта.
Графические примитивы представляют собой процедуры,
осуществляющие рисование в графическом окне. Рисование
осуществляется текущим пером (линии), текущей кистью (за-
ливка замкнутых областей) и текущим шрифтом (вывод строк).
Некоторые процедуры модуля GraphABC, с помощью ко-
торых осуществляется рисование графических примитивов:
procedure SetPixel(x,y:integer; c:Color); –
закрашивает пиксел с координатами (x,y) цветом c;
procedure PutPixel(x,y:integer; c:Color); –
закрашивает пиксел с координатами (x,y) цветом c;
function GetPixel(x,y:integer): Color; – воз-
вращает цвет пиксела с координатами (x,y);
procedure MoveTo(x,y:integer); – устанавливает
текущую позицию рисования в точку (x,y);
procedure LineTo(x,y:integer); – рисует отрезок
от текущей позиции до точки (x,y). Текущая позиция переносит-
ся в точку (x,y);
procedure LineTo(x,y:integer; c:Color); – ри-
сует отрезок от текущей позиции до точки (x,y) цветом c. Теку-
щая позиция переносится в точку (x,y);
procedure Line(x1,y1,x2,y2:integer); – рисует
отрезок от точки (x1,y1) до точки (x2,y2);
procedure Line(x1,y1,x2,y2:integer; c:Color); –
рисует отрезок от точки (x1,y1) до точки (x2,y2) цветом c;
procedure DrawCircle(x,y,r:integer); – рисует
окружность с центром (x,y) и радиусом r;
procedure DrawRectangle(x1,y1,x2,y2:integer); –
рисует границу прямоугольника, заданного координатами про-
тивоположных вершин (x1,y1) и (x2,y2);

82
procedure Circle(x,y,r:integer); – рисует за-
полненную окружность с центром (x,y) и радиусом r;
procedure Rectangle(x1,y1,x2,y2:integer); –
рисует заполненный прямоугольник, заданный координатами
противоположных вершин (x1,y1) и (x2,y2);
procedure TextOut(x,y:integer; s:string); –
выводит строку s в прямоугольник с координатами левого верх-
него угла (x,y);
procedure TextOut(x,y:integer; n:integer); –
выводит целое n в прямоугольник с координатами левого верх-
него угла (x,y);
procedure TextOut(x,y:integer; r:real); – вы-
водит вещественное r в прямоугольник с координатами левого
верхнего угла (x,y).
8. ПАКЕТЫ ПРИКЛАДНЫХ ПРОГРАММ
8.1. Математический пакет Mathcad
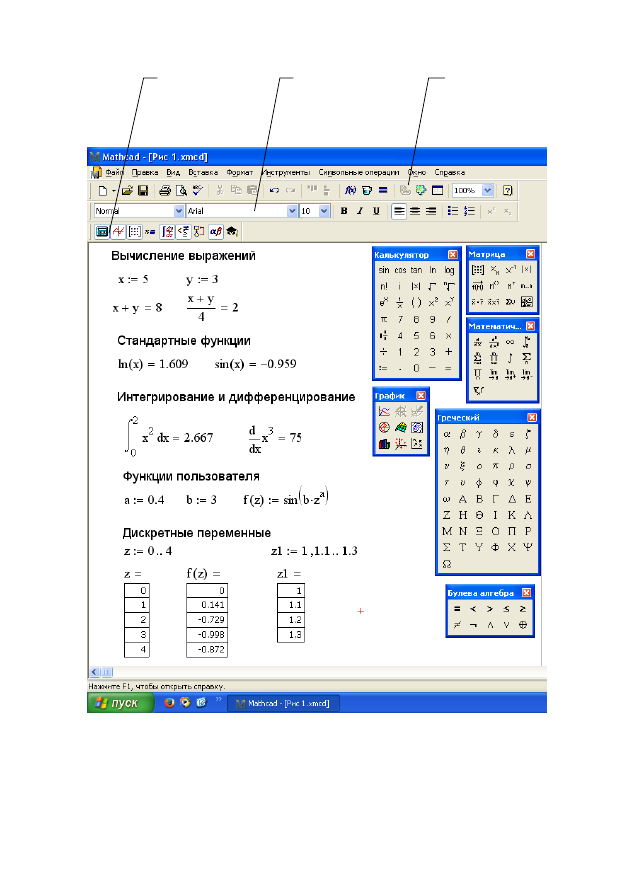
Интерфейс Mathcad аналогичен интерфейсу других Windows-
приложений (рис. 11).
Mathcad предназначен для решения следующих задач [8]:
вычисление результатов математических операций, в ко-
торых участвуют числовые константы, переменные и размерные
физические величины;
операции с векторами и матрицами;
решение уравнений и систем уравнений;
статистические расчеты и анализ данных;
построение графиков;
тождественные преобразования выражений, аналитиче-
ское решение уравнений и систем;
дифференцирование и интегрирование (аналитическое
и численное);
решение дифференциальных уравнений и др.
83
Рис. 11. Вычисления в программе Mathcad
Для ввода элементов формул предназначены дополнитель-
ные панели математической панели инструментов (см. рис. 11):
Математиче-
ская панель
инструментов
Стандартная
панель
инструментов
Панель
инструментов
форматирования

84
График – шаблоны графиков.
Матрица – шаблоны матриц и матричных операций.
Вычисление – операторы присваивания значений и вывода
результатов расчета.
Калькулятор – шаблоны основных математических операций.
Математический анализ – шаблоны дифференцирования,
интегрирования, суммирования.
Булева алгебра – логические (булевы) операторы.
Греческие символы.
Программирование – операторы для создания программных
модулей.
Символьные преобразования – операторы символьных вы-
числений.
Документ программы Mathcad содержит два вида объектов:
формулы и текстовые блоки. В ходе расчетов формулы обраба-
тываются последовательно, слева направо и сверху вниз, а тек-
стовые блоки игнорируются.
Ввод информации осуществляется в месте расположения
курсора. Программа Mathcad использует три вида курсоров. Ес-
ли ни один объект не выбран, используется красный крестооб-
разный курсор, определяющий место создания следующего объ-
екта. При вводе формул используется синий уголковый курсор,
указывающий текущий элемент выражения. Чтобы выделить
элементы формулы, которые в рамках операции должны рас-
сматриваться как единое целое, используют клавишу ПРОБЕЛ.
При каждом ее нажатии уголковый курсор расширяется, охва-
тывая элементы формулы, примыкающие к текущему элементу.
При вводе данных в текстовый блок применяется текстовый
курсор в виде вертикальной черты.
Редактирование введенных выражений производится обыч-
ным для всех Windows-приложений способом.
Mathcad воспринимает прописные и строчные буквы как
разные идентификаторы.
При расчетах по формулам используются следующие опе-
раторы:
оператор присваивания ( := ) (см. рис. 11);

85
оператор вычисления ( = ) (см. рис. 11);
оператор аналитического (символьного) вычисления ()
(рис. 12);
глобальный оператор присваивания ( );
знак логического равенства ( = ).
В Mathcad можно использовать стандартные встроенные
функции (кнопка f(x) на стандартной панели инструментов),
а также функции, определенные пользователем (см. рис. 11).
Функция пользователя определяется следующим образом: слева
указывается название функции, а справа после оператора при-
сваивания (:=) – вычисляемое выражение. Переменные величины,
входящие в правую часть, должны быть записаны в качестве па-
раметров в скобках после имени функции. Все величины из пра-
вой части, не входящие в параметры левой части, должны быть
заданы численно левее и выше функции пользователя.
Для получения таблицы значений функции или ее графика
используются дискретные переменные, определяющие ряд зна-
чений. С помощью дискретной переменной можно задавать как
целые, так и дробные значения переменной, но обязательно рав-
ноотстоящие друг от друга (z и z1 на рис. 11). Дискретная пере-
менная – диапазон – определяется первым, вторым и последним
элементами: :
,
..
b a
x
a a
b
n
, соответственно задает ряд чисел,
где а – первое,
b a
а
n
– второе, b – последнее число, n – число
интервалов, на которые разбит отрезок от a до b. Если интервал
между числами равен 1, то второй элемент отсутствует. Дис-
кретная переменная задается с помощью кнопки m..n – Пере-
менная-диапазон панели инструментов Матрица.
Для построения двухмерного графика функции надо вы-
полнить следующие действия (рис. 12):
1) установить крестообразный курсор в то место, где дол-
жен быть построен график;
2) на панели инструментов График щелкнуть на кнопке
График X-Y;