принадлежащих нормальному распределению, находятся по формуле:

, (4)

где t_p - коэффициент Стьюдента.

Коэффициент t_p в зависимости от доверительной вероятности Р и числа результатов наблюдения n находят по таблица 2.

Таблица 2 Значения коэффициента t_p распределения Стьюдента

Число результа-	Доверительная вероятность Р			Число результа-	Доверительная вероятность Р
тов наб-				тов наб-
людений	0.9	0.95	0.99	людений	0.9	0.95	0.99
n-1				n-1
2	2.92	4.30	9.92	12	1.78	2.18	3.06
3	2.35	3.18	5.84	14	1.76	2.15	2.98
4	2.13	2.78	4.60	16	1.75	2.12	2.92
5	2.02	2.57	4.03	18	1.73	2.10	2.88
6	1.94	2.48	3.71	20	1.72	2.09	2.85
7	1.90	2.37	3.50	22	1.72	2.07	2.82
8	1.86	2.31	3.36	25	1.71	2.06	2.79
9	1.83	2.26	3.25	30	1.70	2.04	2.75
10	1.81	2.32	3.17		1.65	1.96	2.58

Для производственных измерений рекомендуется выбирать Р=0.9,

Р=0.95; для исследовательских целей Р=0.95 и Р=0.99.

В контрольной работе выбирают Р=0.95.

Результат измерения записывают в виде:

(5)

Проверка закона распределения

Правильность выбора нормального распределения, характеризующего рассеяние результатов наблюдений, проверяют при n50 по составному критерию (ГОСТ 8.207-76).

Критерий 1

Вычисляют отношение по формуле:

, (6)

где - смещенная оценка среднего квадратического отклонения, вычисляемая по формуле:

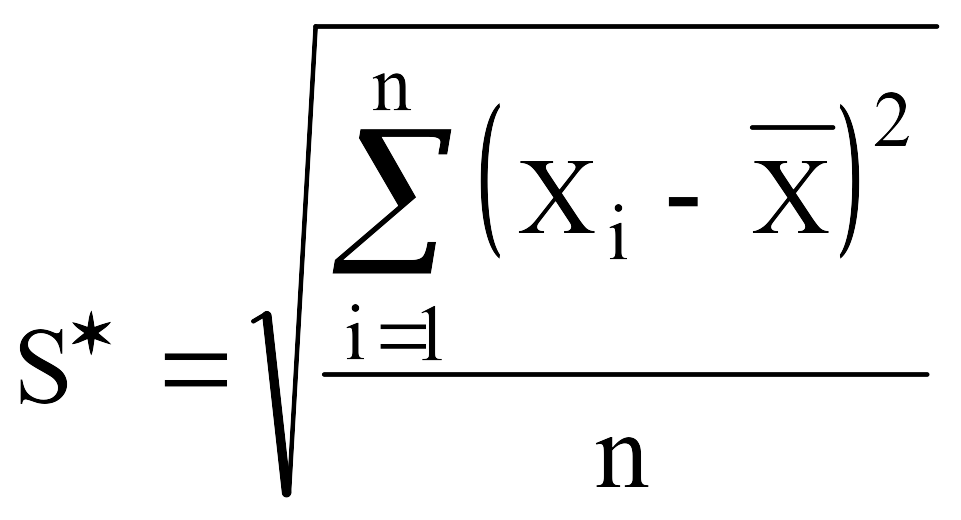(7)

Результаты измерений можно считать распределенными нормаль-но, если d_q1<d_(1-q), где d_q1, d_(1-q1) - квантили распределения, получа-емые из табл. 3 по n, q₁, (1-q₁), причем q₁ - заранее выбранный уровень значимости критерия (для доверительной вероятности Р=0.95 выбираем 5% и 95%, для Р=0.99 выбираем 1% и 99%).

Таблица 3Статистика d

n	(1-q1)100%		q1100%
	1%	5%	95%	99%
16	0.9137	0.8884	0.7236	0.6829
21	0.9001	0.8768	0.7304	0.6950
26	0.8901	0.8686	0.7360	0.7041
31	0.8826	0.8625	0.7404	0.7220
36	0.8769	0.8575	0.7440	0.7167

Критерий 2

Можно считать, что результаты измерений подлежат нормальному распределению. если не более m разностей превзошли значения - верхний квантиль распределения нормированной функции Лапласа, отвечающий значению Р^*/2.

Значение Р^* определяется из таблице 4 по выбранному уровню значимости q₁ и числу наблюдений n.

Z_P^*_/2 определяется по значению интеграла (), приведенной в таблице 5.

---

Таблица 4 Значения Р^* для вычисления

n	m	(1-q1)100%
		1%	5%
1	1	0.98	0.96
11-14	1	0.99	0.97
15-20	1	0.99	0.98
21-22	2	0.98	0.96
23	2	0.98	0.96
24-27	2	0.98	0.97
28-32	2	0.99	0.97
33-35	2	0.99	0.98

Таблица 5 Значения интеграла 


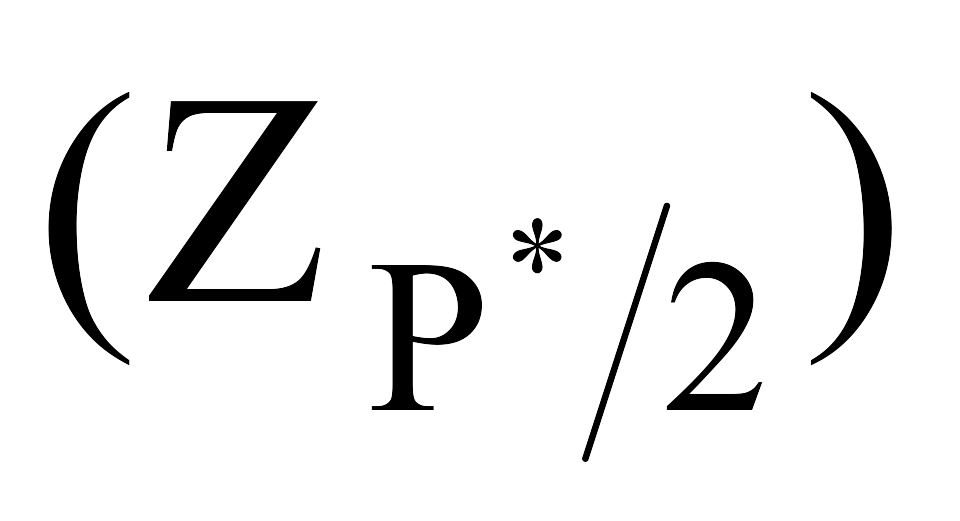
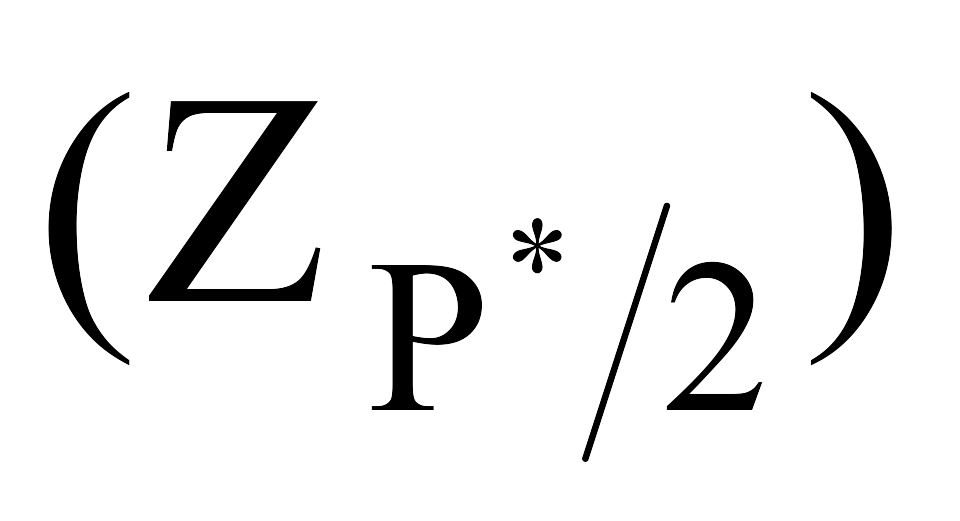
0.485	2.17
0.490	2.34
0.495	2.58

В случае, если хотя бы один из критериев не соблюдается, считают, что распределение результатов измерений не соответствует нормальному.

Отбрасывание грубых замеров

Результаты измерений, содержащие грубые погрешности и промахи, отбрасываются. Наиболее простым, но грубым приемом является отбрасывание результатов наблюдений, содержащих погрешности, превышающие ± 3S.

Более точно проверяют ошибку наблюдений по критерию  (ГОСТ 11.002-73). Находят отношение:

, (8)

Результат сравнивают с величиной , взятой из табл. 6 для числа

наблюдений n и принятого уровня значимости .

Таблица 6 Предельное значение  для исключения грубых погрешностей

Число наблю-	Значение  при  равном			Число наблю-	Значение  при  равном
дений n	0.1	0.05	0.025	дений n	0.1	0.05	0.025
3	1.15	1.15	1.15	10	2.03	2.18	2.29
4	1.42	1.46	1.48	12	2.13	2.29	2.41
5	1.60	1.67	1.72	14	2.21	2.37	2.50
6	1.73	1.82	1.89	16	2.28	2.44	2.58
7	1.83	1.94	2.02	18	2.34	2.50	2.66
8	1.91	2.03	2.13	20 и выше	2.38	2.56	2.71
9	1.98	2.11	2.21

Если U_max> или U_min>, то сомнительный результат измерений следует считать грубым и его надо отбросить. Затем вновь вычисляют

Запись результата измерения

Окончательно полученный результат измерений записывают по формуле (5).

2.2.2. Определение класса точности измерительного прибора

Класс точности присваивается средствам измерений в соответствии с ГОСТ 8.401-80. Класс точности электроизмерительных приборов, манометров и других средств измерений определяется приведенной основной погрешностью:

(10)

где  - приведенная основная погрешность, в процентах,

 - абсолютная основная погрешность, выраженная в единицах измеряемой величины,

X_H - нормирующий показатель, равный конечному значению шкалы прибора при нулевой шкале, в единицах измеряемой величины.

---

При постоянном значении технологического параметра Если наблюдаются значительные отклонения, например при бурении, тогда Класс точности прибора выбирается из ряда чисел (1, 1.5, 2, 2.5, 4, 5, 6)10^j , которые равны пределам погрешностей, выраженным в процентах. При этом j=1,0,-1,-2,-3, -4.

В заданиях по вариантам указан интервал отклонения технологического параметра, равный 2. Значение параметра определяется как результат оценки равноточных измерений , полученный в пер­вой части контрольной работы.

При измерении уровня погрешность измерения выражают в форме абсолютной основной погрешности  .

2.2.3. Выбор промышленного измерительного прибора

Выбор прибора требует учета многих факторов: диапазона и точности измерения, формы выдачи показаний, условий эксплуатации, надежности, стоимости и т.д. Основными из них являются класс точ­ности и диапазон измерений.

Для конкретного технологического процесса согласно задания по данным расчетов контрольной работы № 1 выбирается промышленный измерительный прибор. При этом необходимо дать технико-экономическое обоснование выбранного прибора.

Выбор производится по каталогам, справочникам и учебной лите­ратуре. В контрольной работе обязательна ссылка на литературный источник.

2.2.4. Пример выполнения практической работы № 1

Температура в лабораторной термокамере находится в пределах от 135.1 до 138.5°С.

Результаты равноточных измерений термо-ЭДС термопары типа ХК следующие (в милливольтах):

9.631	9.623	9.620	9.625	9.618	9.619	9.629
9.632	9.625	9.620	9.618	9.616	9.628	9.639
9.606	9.624	9.623	9.625

Требуется: 1. Оценить точность результатов измерений; 2. Определить класс точности термометра;

3. Выбрать измерительный прибор.

Расчет результата измерения

Исходные данные и результаты вычислений представлены в таблице 7.

Таблица 7 Расчет точности результатов измерений

№	Термо ЭДС, мВ		min, max
1	9.631	0.008		6410-6	0.008<0.016	0.008<0.021
2	9.619	-0.004		1610-6
3	9.618	-0.005		2510-6
4	9.624	0.001		110-6
5	9.623	0.000		0
6	9.629	0.006		3610-6
7	9.616	-0.007		4910-6
8	9.623	0.000		0
9	9.620	-0.003		910-6	<0.016	<0.021
10	9.632	0.009		8110-6
11	9.628	0.005		2510-6
12	9.625	0.002		410-6
13	9.625	0.002		410-6
14	9.625	0.002		410-6
15	9.639	0.016	max	25610-6
16	9.618	-0.005		2510-6
17	9.620	-0.003		910-6
18	9.606	-0.017	min	28910-6	0.017>0.016	0.017<0.021
	173.221	/0.095/		89710-6	m=1	нет грубых промахов

---

Среднее арифметическое результата измерений вычисленное по формуле (1):

Среднее квадратическое отклонение S результата наблюдения (2):

Cреднее квадратическое отклонение результата измерения (3):

Смещенная оценка S^* среднего квадратического отклонения (7):

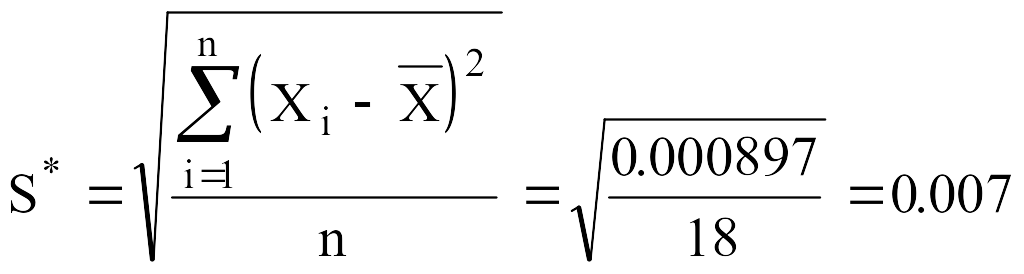
Коэффициент Стьюдента t_p выбирается по таблице 2 для n-1=17 и P=0.95, t_p=2.11.

Доверительные границы  находят по формуле (4):

Результат измерения (5):

мВ (18; 0.95)

Проверка закона распределения

По критерию 1 вычисляют отношение (6):

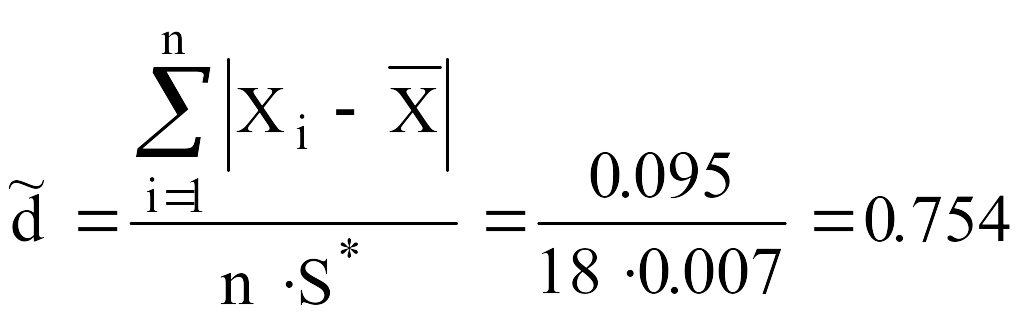
Квантили распределения выбираются по таблице 3.

d_q1=0.726< =0.754<d_(1-q1)=0.883

Неравенство выполняется. Критерий 1 соблюдается.

По критерию 2 определяют число m.

Значение P^* и число m выбирается по таблице 4.

P^*=0.98; m=1. Тогда

По табл. 5 выбирается верхний квантиль распределения

Вычисляют . Из таблице 7 следует, что для замера № 18 неравенство не выполняется, т.е. m=1.

Критерий 2 соблюдается, а распределение результатов соответствует нормальному.

Отбрасывание грубых замеров

Грубых промахов, превышающих 3S, в результатах измерений нет (таблице 7).

Вычисляют отношение (8):

;

Предельное значение  выбирается по таблице 6: =2.5.

U_max=2.286<=2.5; U_min=2.428<=2.5,

т.е. грубых замеров в исходных данных нет.

Запись результата измерения

Результат измерения термо-ЭДС записывается:

X=9.6230.004 мВ (18; 0.95)

Определение класса точности термометра

В примере интервал отклонения температуры в термокамере составляет 138.5-135.1=3.4С, что равно 2. Абсолютная основная погрешность составит =1.7С.

Вычисление мВ для термопары типа ХК соответствует измеряемой температуре 136.8°С (определено по градуировочной характеристике термоэлектрического термометра типа ХК).

Процесс стабильный, выбираем нормирующий показатель

°С

Приведенная основная погрешность вычисляется по формуле (10):

Для измерения температуры в термостате выбирается термометр класса точности 1.

Выбор промышленного измерительного прибора

С учетом того, что измеряется температура в лабораторной термокамере и условия регистрации показаний не оговорены, выбирается лабораторный стеклянный технический ртутный термометр со шкалой 101-200С, ценой деления шкалы 1С (Иванова Г.М. и др. “Тепло­технические измерения и приборы”. М.: Энергоатомиздат, 1984, с.21).

---

Смотрите также файлы

• Задание на лабораторную работу №2.doc

• Задание на лабораторную работу №1.doc

• Задание на итоговую контрольную работу.doc

• Лекция 6. Приборы для управления технологическими процессами производства.doc

• Лекция 5. Приборы для обработки сигналов.doc