Файл: Лекция 2. Математический аппарат, используемый в задачах искусственного интеллекта.doc
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Системы искусственного интеллекта
Добавлен: 29.10.2018
Просмотров: 598
Скачиваний: 9
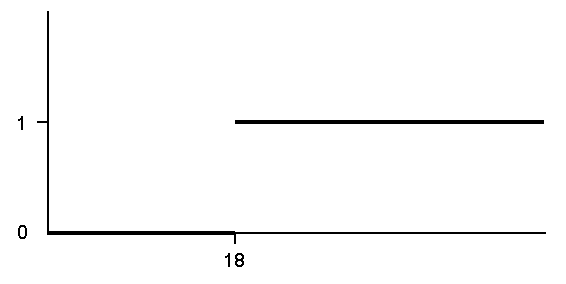
Рис.2.2. Функция принадлежности четкого множества.
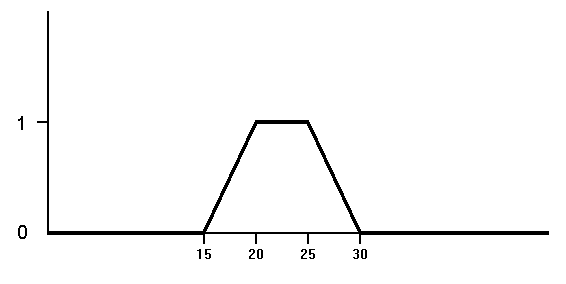
Рис.2.3. Функция принадлежности нечеткого множества
и в таком случае описывается формулами:
при y < 15 P(y) = 0;
при 15 < y < 20 P(y) = (y - 15)/5;
при 20 < y < 25 P(y) = 1;
при 25 < y < 30 P(y) = (30 - y)/5;
при y > 30 P(y) = 0.
Иными словами, при возрасте менее 15 и старше 30 лет человек молодым заведомо не является, а в промежутке от 20 до 25 лет - заведомо является. В промежутке от 15 до 20 лет статус МОЛОДОГО ЧЕЛОВЕКА плавно возрастает, принимая значения от 0 до 1, а в промежутке от 25 до 30 лет - убывает от 1 до 0.
Для того, чтобы описать нечеткое множество МОЛОДОЙ ЧЕЛОВЕК, следует указать все его элементы с указанием степени принадлежности элемента множеству. Это делается с помощью записи
МЧ=0.2/16+0.4/17+0.6/18+0.8/19+1/20+1/21+1/22+1/23+1/24+1/25+0.8/26+0.6/27+0.4/28+0.2/29
В тех случаях, когда это не может привести к путанице, можно использовать обычное обозначение коэффициентов, принятое в алгебре. Например, если множество Z состоит из элементов a, b, c, d, e с функцией принадлежности
Z = 0.1/a+0.5/b+0.9/c+0.7/d+0.5/e
это может быть также записано во форме
Z = 0.1a+0.5b+0.9c+0.7d+0.5e
2.2.1.Операции с нечеткими множествами.
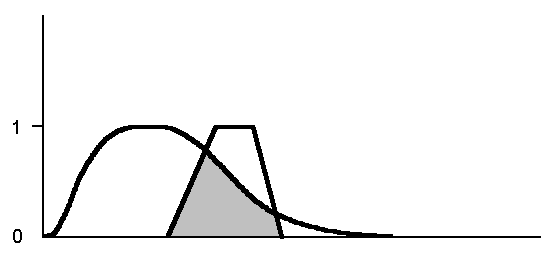
К нечетким множествам, как и к четким, применимы операции объединения, пересечения и дополнения. Если считать, что в универсальном множестве U выделены два нечетких множества A и B с функциями принадлежности f и g, то их объединение имеет функцию принадлежности h
h(u) = max (f(u), g(u))
Например, если
U = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
A = 0.8/0+0.7/1+0.6/2+0.4/3+0.2/4+0.1/5+0.1/6+0.1/7
B = 0.1/3+0.3/5+0.5/7+0.7/8+0.9/9
то A B имеет вид
A B = 0.8/0+0.7/1+0.6/2+0.4/3+0.2/4+0.3/5+0.1/6+0.5/7+0.7/8+0.9/9
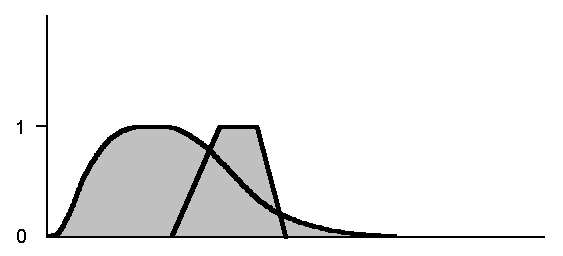
Аналогично, функция принадлежности для пересечения нечетких множеств A и B имеет вид min (f(u), g(u)). В том же примере
A B = 0.1/3+0.1/5+0.1/7
Дополнение множества имеет функцию принадлежности, вычисляемую как дополнение до 1 функции принадлежности исходного множества. Так, дополнение множества A имеет функцию принадлежности
A = 0.2/0+0.3/1+0.4/2+0.6/3+0.8/4+0.9/5+0.9/6+0.9/7+1/8+1/9
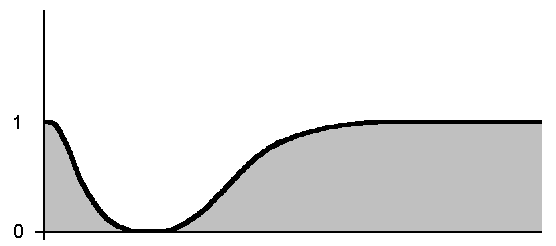
(Легко заметить, что если множества являются четкими, т.е. функция принадлежности принимает только значения 0 и 1, то построенные указанным образом функции принадлежности описывают обычные операции объединения, пересечения и дополнения множеств.)
НЕЧЕТКАЯ ЛОГИКА
В отличие от обычной логики, где существуют только два значения истинности утверждения ИСТИНА и ЛОЖЬ, в нечеткой логике "значение истинности" утверждения может принимать и промежуточные значения. Считается, что ИСТИНА имеет значение 1, ЛОЖЬ - 0, и истинность любого утверждения u, обозначаемая (u), находится в промежутке между этими значениями.
В нечеткой логике существуют те же логические операции конъюнкции, дизъюнкции и отрицания, однако они определяются иначе, чем в обычной логике. Если истинность логических операций конъюнкции, дизъюнкции и отрицания в обычной логике задается таблицами истинности, то в нечеткой логике она задается формулами. Если истинность утверждения u равна (u), а v - (v), то истинность конъюнкции, дизъюнкции и отрицания выражается формулами
(u v) = min ((u), (v)), (u v) = max ((u), (v))
(u) = 1 - (u)
При этом свойства нечетких операций в значительной степени сходны со свойствами операций в обычной логике, в частности:
(u v) = (v u) , (u v) = (v u)
((u v) w) = (u (v w)) , ((u v) w) = (u (v w))
((u)) = (u), ((u v)) = (u v)
((u v)) = (u v), ((u v) w) = ((u w) (v w))
((u v) w) = ((u w) (v w)), (0 u) = (u)
(1 u) = 1, (0 u) = 0, (1 u) = (u)
(Однако аналогия не является полной - например, аналоги формул u u = 0 и u u = 1 в нечеткой логике неверны.)
Используемые в логическом выводе формулы импликации вида A B также могут быть нечеткими, т.е. их уровень истинности может быть меньше 1. В этом случае уровень истинности заключения вычисляется как произведение уровня истинности посылки на уровень истинности импликации. Например, если (A) = 0.9, а (A B) = 0.8, то (B) = 0.72.