Лекция 3. Логические рассуждения.

Рассуждением или умозаключением обычно называют ряд мыслей, изложенных в логически последовательной форме.

Агент должен уметь находить интересующие его состояния среды (целевые состояния), если он что-либо знает о других ее состояниях. Определение целевых состояний осуществляется с помощью поиска или рассуждений в пространстве состояний.

3.1.Рассуждения в пространстве состояний среды.

В коммунальной квартире две старушки занимают по комнате. Комнаты находятся в общем коридоре, который имеет выход на лестничную клетку. Одна из комнат расположена слева (левая комната) от выхода, а другая — справа (правая комната). В коридоре живет кот, которого обе старушки одинаково любят и балуют, оставляя ему кусочки сыра. Каждая старушка кладет кусочек сыра у двери своей комнаты. Кот отдыхает либо у левой комнаты (слева), либо у правой (справа).

Множество всех состояний этой среды (среды кота) можно представить табл. 3.1, в столбцах которой для каждого состояния среды указаны - местонахождение кота (слева или справа), наличие или отсутствие кусочка сыра (да или нет) у соответствующей комнаты.

Таблица 3.1

Состояние	Местонахождение кота	Наличие сыра
		слева	справа
b1	Слева	Да	Да
b2	Справа	Да	Да
b3	Слева	Да	Нет
b4	Справа	Да	Нет
b5	Слева	Нет	Да
b6	Справа	Нет	Да
b7	Слева	Нет	Нет
b8	Справа	Нет	Нет

Состояние b₁ означает, что кот находится около левой комнаты и около обеих комнат лежит по кусочку сыра, состояние b₂ — кот находится около правой комнаты и около обеих комнат снова лежит по кусочку сыра и т.д.

Кот может совершать в один и тот же момент времени только одно из следующих действий: переходить к дверям левой комнаты, переходить к дверям правой комнаты и съедать кусочек сыра около той комнаты, где он находится.

Эти действия обозначим с₁ = Идти налево, с₂ = Идти направо и с₃ = Съесть, соответственно. Если среда находится в одном из состояний, перечисленных в табл. 3.1, и кот совершает какое-либо из действий, то нетрудно определить в какое состояние после выполнения действия перейдет среда.

Будем полагать, что нам известно состояние, называемое начальным, с которого могут начаться изменения среды при действиях кота.

---

Пусть, например это будет состояние b₁. Будем изображать состояния

кружочками с обозначением состояния внутри кружочка.

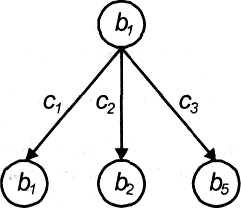
Рис. 3.1. Допустимые переходы из начального состояния b₁

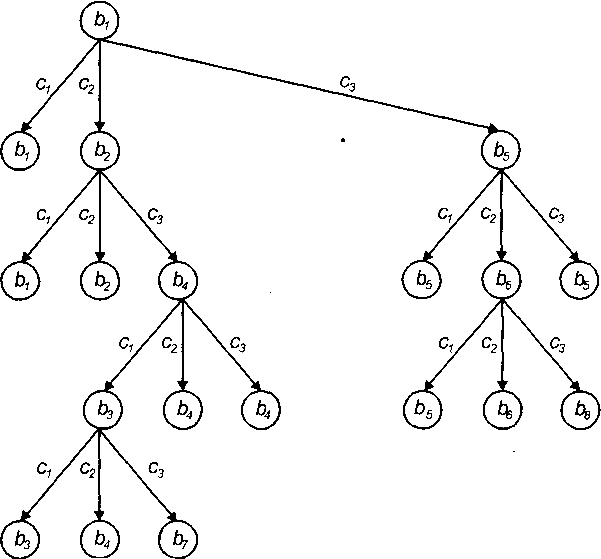
Рис. 3.2. Дерево переходов

Переход из одного состояния в другое, происходящий в результате действия, будем изображать стрелкой, ведущей в это другое состояние и помеченной соответствующим действием. Так, на рис.3.1 изображены все переходы из состояния b₁ в результате действий с₁,с₂ , с₃ .

На рис. 3.2 показано дерево всех дальнейших переходов, являющееся продолжением элементарного дерева на рис. 3.1. Построение каждой ветви дерева прекращено на том состоянии, которое встречается повторно на пути, ведущем в него из начального состояния.

3.1.1. Постановка задачи

Цель кота — не оставить ни одного кусочка сыра, где бы он изначально ни находился. В терминах состояний среды целью кота является перевод ее с помощью своих действий (реакций) в одно из состояний b₇ или b₈ . Состояния, в которые с помощью набора допустимых действий необходимо перевести среду, называются целевыми. Процесс определения этих состояний называют формулировкой цели. Будем полагать в рамках нашего примера, что каждое восприятие совпадает с одним из состояний. Задачей агента является

нахождение последовательности действий или пар восприятие—действие, ведущих на дереве переходов из начального состояния в целевые. Процесс нахождения этих последовательностей называют поиском, выводом или рассуждением. Постановкой задачи называют задание всех состояний и действий, которые можно использовать для решения задачи, начального состояния и целевых состояний, а также всех допустимых переходов между состояниями при выполнении действий. Для среды кота постановка задачи уже осуществлена. Все состояния, которые могут использоваться при решении задачи, перечислены в табл. 3.1. Целевыми состояниями являются состояния b₇, b₈. Все допустимые переходы между состояниями показаны на рис. 3.2. Из рисунка ясно, что решениями задачи является последовательность b₁/c₂, b₂/c₃,b₄/c₁,b₃/c₃, в результате выполнения которой агент (кот) переведет среду в состояние b₇, и последовательность b₁/c₃, b₅/c₂, b₆/c₃, в результате выполнения которой среда окажется в состоянии b₈.

3.1.2. Формализация вывода средствами логики высказываний

Для записи задачи на языке исчисления высказываний введем три логические переменные х_к, х_л, х_п .

Истинное значение первой из них означает, что кот находится у левой комнаты, а ложное, что он находится у правой комнаты;

истинное значение переменной х_л означает, что кусочек сыра лежит около левой комнаты, а ложное, что его там нет;

истинное значение переменной х_п означает, что кусочек сыра лежит около правой комнаты, а ложное, что его там нет.

В результате таких обозначений табл. 3.1 можно заменить на табл. 3.2. Каждое состояние среды можно рассматривать как комбинацию (отношение) простейших свойств объектов, задаваемых значениями отдельных логических переменных. Так, состояние b₁ соответствует комбинации свойств кота и кусочков сыра, состоящей в том, что кот находится в левой комнате, и в это же самое время около левой и правой комнат находится по кусочку сыра. На русском языке эту комбинацию можно выразить предложением: «Кот находится около левой комнаты, кусочек сыра лежит около левой комнаты и кусочек сыра лежит у правой комнаты». В соответствии с уже приведенной выше интерпретацией логических переменных х_к, х_л, х_п это предложение можно представить формулой , которая истинна в единственном случае - все логические переменные, входящие в нее, истинны, т.е. среда находится в состоянии b₁. Формулы такого типа, являющиеся конъюнкцией переменных с отрицанием или без него, называют элементарными конъюнкциями. Если среда находится в состоянии b₂, то истинна формула ^{и т.д.}

---

Элементарную конъюнкцию, в которую входит по одному разу каждая переменная, определяющую состояние среды, с отрицанием или без отрицания, называют полной конъюнкцией, или конституентой.

Аналогично тому, как были введены логические переменные х_к, х_л, х_п, введем логические переменные z ₁, z₂, z₃ для действий кота “Идти налево”, “Идти направо”, “Съесть “,соответственно. Переменная принимает истинное значение, если выполняется соответствующее ей действие. В противном случае она принимает ложное значение.

Таблица 3.2

Состояние	Переменные			Формула, описывающая состояние
	xk	xл	xп
b1	И	И	И
b2	Л	И	И
b3	И	И	Л
b4	Л	И	Л
b5	И	Л	И
b6	Л	Л	И
b7	И	Л	Л
b8	Л	Л	Л

Для простоты будем полагать, что кот не может одновременно выполнять сразу более одного действия.

Таблица 3.3

Переход			Импликация, соответствующая переходу
Исходное состояние	Действие	Результирующее состояние
b1	c1	b1
b1	c2	b2
b1	c3	b5
b2	c1	b1
b2	c2	b2
b2	c3	b4
b3	c1	b3
b3	c2	b4
b3	c3	b7
b4	c1	b3
b4	c2	b4
b4	c3	b4
b5	c1	b5
b5	c2	b6
b5	c3	b5
b6	c1	b5
b6	c2	b6
b6	c3	b8

Рассмотрим теперь, как могут быть выражены в виде формул переходы среды из одного состояния в другое при совершении котом того или иного действия. Так, если кот находился в состоянии b₁, и выполнил действие “Идти направо”, то среда перейдет в состояние b₂ . Факт нахождения кота в состоянии b₁, и выполнение им в это время действия “Идти направо” означает истинность формулы , а факт перехода состояния b₁ при выполнении действия «идти направо» в состояние b₂ будем интерпретировать как истинность формулы , что позволяет при истинности сделать заключение об истинности . Точно так же можно выразить в виде аналогичных формул все остальные переходы, показанные на рис. 3.2. Представим их в виде табл. 3.3. В первых трех столбцах этой таблицы указаны переходы, имеющиеся на рис. 3.2, а в последнем -формулы, соответствующие переходам.

3.1.3. Поиск решения

Решения задачи для среды кота практически очевидны, когда построено дерево переходов состояний среды, по которому легко проследить пути, ведущие в целевые состояния из начального. В реальных задачах это дерево может быть очень большим, вследствие чего нецелесообразно использовать стратегию поиска, согласно которой необходимо сначала получать дерево целиком. Вместо этого используются другие более эффективные стратегии поиска, речь о которых пойдет в главе 4. Однако, какая бы из этих стратегий не применялась, элементарным шагом поиска является переход из одного состояния среды в другое и анализ состояния, в которое переход был осуществлен, на принадлежность к числу целевых. Каждый допустимый переход из состояния b_i. после совершения действия с_j в состояние b_k можно задавать с помощью правила перехода: « Если среда находится в состоянии b_i. и совершается действие с_j, то она должна перейти в состояние b_k».

---

Совокупность правил подобного типа используется в процессе поиска. Одной из очевидных, но чрезвычайно неэкономных стратегий поиска, позволяющей найти все решения для среды кота, может быть следующая.

1.Образовать множество В = {b₁}, состоящее из одного начального состояния b₁.

2. Для каждого состояния множества В и каждого действия с найти, согласно соответствующим правилам перехода, все состояния b_k, в которые переходит среда. Совокупность всех таких состояний, за исключением тех, которые уже встречались в ранее образованных множествах В, принять за новое множество В.

3. Проверить, нет ли среди элементов этого множества целевых состояний. Если целевых состояний нет, то перейти к п. 2. Если целевые состояния есть, то выписать в порядке использования правил все последовательности действий, которые привели к целевым состояниям, удалить эти состояния из множества В и перейти к выполнению следующего пункта.

4. Проверить, все ли целевые состояния найдены. Если найдены все, то прекратить поиск. Если найдены не все, то перейти к п. 2.

Проиллюстрируем на примере среды кота применение этой стратегии. Правила перехода выписывать не будем, поскольку в нашем распоряжении уже есть дерево переходов (см. рис. 2.2).

Итак, вначале В = {b₁}. После выполнения п. 2 имеем совокупность состояний b_{1 ,}b₂, b₅ . В этой совокупности нет ни одного целевого состояния, а состояние b₁ уже встречалось. Поэтому, согласно п. 3, принимаем В = {b₂,b₅} и переходим к выполнению п. 2. В результате получаем совокупность состояний b₁,b₂, b₄, b₅, b₆ , среди которых опять нет целевых, а b₁, b₂ , b₆ уже встречались. Поэтому В = {b₄, b₆ } и снова возвращаемся к п. 2. После очередного выполнения этого пункта имеем совокупность состояний b₃, b₄, b₅, b₆, b₈ . Среди этих состояний b₄, b₅, b₆ уже встречались, а состояние b₈, является целевым. В это состояние ведет единственная последовательность действий с₃, c₂ , c₃. Однако еще не все целевые состояния найдены, а именно не найдено состояние b₇ . Поэтому в соответствии с п. 4 продолжим поиск, вновь переходя к п. 2 с множеством В = {b₃}. В результате получим совокупность состояний b₃, b₄, b₇, среди которых b₃, b₄ уже встречались, а b₇ - целевое. Последовательностью действий, ведущих в состояние b₇, является c₂ c₃ c₁ c₃. И так, все целевые состояния найдены, решение задачи в виде последовательности действий, ведущих в эти состояния, получено. Поиск на этом прекращается.

3.2.Нечеткий логический вывод.

Выше было определено, что правила СИИ формулируются экспертом. Но эксперт не всегда может точно определить, произойдет какое – либо событие , или нет. Например, врач ставит на основании своих наблюдений над пациентом определенный диагноз. Опыт врача во многих случаях с большой точностью позволяет определить заболевание пациента. Но он может и ошибиться, поэтому часто рассматри­ваются и другие диагнозы.

---

Люди не всегда могут отве­тить на вопросы точно. Можно ли узнать, какая у человека температу­ра, если он говорит, что слегка заболел? Скорее всего, нет. Такие слова, как высокий, горячий и легкий, представляют собой лингвистические переменные, которые нельзя определить одним значением.

Лингвистическая переменная состоит из названия переменной, например, ПРОЦЕНТНАЯ СТАВКА и ее значений, например, РАСТЕТ, ПАДАЕТ.

Использо­вание этих понятий при формулировании правил называется нечеткой логикой.

Нечеткий логический вывод может рассматриваться как расширение обычного логического вывода. В обычном логическом выводе производится применение некоторых правил логического вывода (которые считаются истинными) к некоторым посылкам (которые также считаются истинными), что в результате дает выводы, считающиеся достоверными. В нечетком же логическом выводе и исходные посылки, и правила вывода могут иметь произвольный уровень истинности в промежутке от 0 до 1, соответственно и получаемые результаты также могут быть более или менее достоверны.

В качестве примера рассмотрим влияние квартирной платы и цен на продукты питания на уровень жизни семьи. Это влияние описывается следующими утверждениями.

1. ЕСЛИ К_П незначительно растет, ТО У_Ж_1 незначительно падает. ( = 0.9)

2. ЕСЛИ К_П незначительно растет, ТО У_Ж_1 не падает. ( = 0.1)(Если перестают платить)

3. ЕСЛИ К_П значительно растет, ТО У_Ж_1 значительно падает. ( = 0.5)

4. ЕСЛИ К_П значительно растет, ТО У_Ж_1 не падает. ( = 0.5)

5. ЕСЛИ Ц_П незначительно растут, ТО У_Ж_2 незначительно падает. ( = 1)

6. ЕСЛИ Ц_П значительно растут, ТО У_Ж_2 значительно падает. ( = 1)

7. ЕСЛИ У_Ж_1 незначительно падает И У_Ж_2 незначительно падает, ТО У_Ж незначительно падает. ( = 1)

8. ЕСЛИ У_Ж_1 незначительно падает И У_Ж_2 значительно падает ИЛИ У_Ж_1 значительно падает И У_Ж_2 значительно падает, ТО У_Ж значительно падает. ( = 1)

9. ЕСЛИ У_Ж_1 значительно падает И У_Ж_2 значительно падает, ТО У_Ж очень значительно падает. ( = 1)

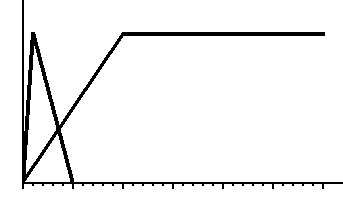
Условия К_П НЕЗНАЧИТЕЛЬНО РАСТЕТ и К_П ЗНАЧИТЕЛЬНО РАСТЕТ являются размытыми и выражаются в зависимости от количества процентов роста p следущими формулами.

При 0 < p < 2  (К_П НЕЗНАЧИТЕЛЬНО РАСТЕТ) = p / 2.

При 2 < p < 4  (К_П НЕЗНАЧИТЕЛЬНО РАСТЕТ) = 1.

При 4 < p < 10  (К_П НЕЗНАЧИТЕЛЬНО РАСТЕТ) = (10 - p) / 6.

При p > 10  (К_П НЕЗНАЧИТЕЛЬНО РАСТЕТ) = 1.

При p < 5  (К_П ЗНАЧИТЕЛЬНО РАСТЕТ) = 0.

При 5 < p < 15  (К_П ЗНАЧИТЕЛЬНО РАСТЕТ) = (p - 5) / 10.

При p > 15  (К_П ЗНАЧИТЕЛЬНО РАСТЕТ) = 1.

Условия Ц_П НЕЗНАЧИТЕЛЬНО РАСТУТ и Ц_П ЗНАЧИТЕЛЬНО РАСТУТ также являются размытыми и выражаются формулами

При 0 < p < 1  (Ц_П НЕЗНАЧИТЕЛЬНО РАСТУТ) = p.

При 1 < p < 5  (Ц_П НЕЗНАЧИТЕЛЬНО РАСТУТ) = (5 - p) / 4.

При 0 < p < 10  (Ц_П ЗНАЧИТЕЛЬНО РАСТУТ) = p / 10.

При p > 10  (Ц_П ЗНАЧИТЕЛЬНО РАСТУТ) = 1.

При использовании нечеткой логики для каждой формулы вводятся целый спектр возможных значений, лежащих между 0 (ЛОЖНО) и 1 (ИСТИННО), и правила вычисления этих значений. Вычисленные таким образом значения определяют степень истинности формул. Рассмотрим основополагающие понятия нечеткого множества и функции принадлежности.

---

Смотрите также файлы

• Лекция 2. Математический аппарат, используемый в задачах искусственного интеллекта.doc

• Лекция 1. Основные понятия систем искусственного интеллекта.doc

• Задание на практическую работу №2.doc

• Задание на практическую работу №1.doc

• Задание на лабораторную работу №2.doc