Файл: СУРОВА.docx

1. Виділяють такі основні ознаки системності:

1) цілісність;

2) структурованість;

3) взаємозв’язок частин;

4) підпорядкованість частин одній меті;

5) алгоритмічність діяльності (у логічному розумінні).

2. Системний підхід – це загальнонауковий методологічний напрямок, в рамках якого методологічний напрямок, в рамках якого розробляються методи та засоби теоретичного дослідження складноорганізованих об’єктів (систем). Системний підхід (на відміну від системного аналізу) спрямований на теоретичне розгортання знання, на формування та розвиток специфічних предметів наукового дослідження.

3. Методологічні процедури, що розробляються системним підходом, відносяться до вивчення законів:

1) утворення цілого;

2) будови цілого;

3) функціонування цілого;

4) росту і розвитку цілого;

5) співвідношення між об’єктом (явищем) та родовою системою (метасистемою);

6) відношення між об’єктом та системою інших мета систем

4. Методологія системного підходу базується на таких основних принципах (принцип – це основне вихідне положення науки, вчення, світогляду).

1. . Принцип багатоплановості 2. Принцип багатовимірності, 3. Принцип багаторівневості4. Принципи різнопорядковості5. Принцип динамічності

5. 1. Принцип багатоплановості полягає в тому, що будь-який об’єкт (явище) розглядається в декількох планах (аспектах):

а) як деяка якісна одиниця, що має свої специфічні особливості;

б) як частина своєї видородової макросистеми, закономірностям якої підпорядковується об’єкт, що вивчається, або явище;

в) у плані мікросистем, закономірностям яких він теж підпорядковується

6. Принцип багатовимірності, полягає в тому що будь-який складний об’єкт характеризується великою сукупністю властивостей, об’єднаних у групи (кластери), кожен з яких описує ті чи інші його особливості. Об’єктивний „портрет” події можна отримати тільки в тому випадку, коли досліджуються всі групи властивостей та зв’язки між ними.

7. 3. Принцип багаторівневості (ієрархічності) полягає в тому, що вивчення складних систем (об’єктів, явищ) повинно базуватися на уявленні про ієрархічність (просту чи складну) їх структури. Ієрархічну структуру мають не тільки моделі складу системи (системи-підсистеми-елементи), але також властивості, якості цих систем та критерії, що застосовуються для їх оцінки.

8. 4. Принципи різнопорядковості властивостей полягає в тому, що ієрархічність будови системи та її властивостей породжує закономірності різного порядку. Одні закономірності притаманні всім рівням ієрархії, тобто всій системі, інші належать тільки деякій групі рівнів, треті характерні тільки для елементів одного рівня, четверті – тільки для окремих елементів одного рівня.

9.Принцип динамічності полягає в тому, що системний підхід потребує розгляду об'єкта, що вивчається, чи явища в їх розвитку, на всіх етапах їх „життєвого циклу”.

10. Теорія систем – це науковий напрямок, пов’язаний з розробкою методології розв’язку проблем прикладного характеру

11. З практичної точки зору теорія систем є системою методів дослідження чи проектування складних систем, пошук, планування та реалізації змін, призначених для ліквідації проблем

12. З методологічної точки зору теорія систем є прикладною діалектикою, оскільки реалізує ідеї діалектики стосовно конкретних практичних задач, особливість яких полягає в необхідності виявлення причин їх складності, та усунення цих причин.

13. Теорія систем спирається на самі загальні системні уявлення, так як:

1) система та підсистема;

2) система та середовище;

3) входи та виходи системи;

4) цілі системи;

5) функції та властивості системи;

6) умови та засоби досягнення цілей;

7) якість системи, чи адекватність її функціонування (діяльності).

14. складність – це властивість об'єкта (системи, процесу, явища, ситуації), що виражається в раптовості, непередбачуваності; або не пояснювальному характері, випадковості; „анти інтуїтивності” його поведінки.

15. Будь-яка система характеризується:

1) цілісністю;

2) відносною відособленістю від навколишнього середовища (межами);

3) зв’язками із зовнішнім середовищем;

4) наявністю частин та зв’язків між ними (структурованістю);

5) підпорядкованістю усієї організації системи деякій цілі (чи сукупності цілей).

16. трьох форм опису):

1) предметної;

2) функціональної;

3) історичної.

17. Предметний аспект системного дослідження передбачає двох взаємопов’язаних задач:

1) виявлення елементарного складу системи (компонентний аналіз);

2) виявлення відношень (зв’язків) між елементами системи (структурний аналіз).

18. Структурний аналіз є діалектично пов’язаним з аналізом складу системи і включає дві основні задачі:

1) виявлення закономірностей взаємозв’язку елементів системи;

2) виявлення ступеня складності системи.

19. Функціональний аспект теорії систем включає розкриття внутрішнього та зовнішнього функціонування системи.

20. Внутрішнє функціонування системи досліджується у плані здатності виконання нею своєї зовнішньої функції.

21. Зовнішнє функціонування системи досліджується для виявлення адаптивності (пристосування середовища до системи) активності системи.

22. Історичний опис системи включає два види дослідження (опису): генетичний та прогностичний

23. Генетичне дослідження присвячене вивченню походження даної системи, процесам його формування та етапам його життєвого циклу до того моменту, коли дослідник робить систему предметом своєї уваги.

24. Прогностичне дослідження пов’язане з розглядом перспектив подальшого розвитку системи, її можливого стану та очікуваної поведінки на прогнозований відрізок часу

25. У теорії систем розрізняють ціленаправлені та цілеспрямовані системи

26. Перша група систем (холодильники, телевізори, літаки та ін.) поводять себе як запрограмовані роботи

27. До другої групи можна віднести тваринний світ та людину, університет, політичну партію та ін.

28. Основна відмінність цих систем полягає в багатоманітності способів реакції на дію зовнішнього середовища. У цілеспрямованих системах ці способи обмежені, а у цілеспрямованих систем вибір достатньо великий

29.На шляху здійснення цілей системи, тобто реалізації призначень системи (особливо соціотехнічних систем), часто виникають бар’єри, пов’язані з внутрішніми обмеженнями системи та обмеженнями середовища

30. До внутрішніх обмежень можна віднести:

1) неадекватність сприйняття системи;

2) слабка структурованість проблем;

3) конфлікт у системі

31. До обмежень середовища відносять:

1) недоліки планування, пов’язані з неясністю цілей;

2) турбулентність середовища (складність системи відношень елементів середовища і системи);

3) запізнювання зворотного зв’язку із середовищем.

32. Під функцією розуміють зовнішній прояв властивостей об'єкта у даний системі відношень

33. У системному аналізі функцію об'єкта ототожнюють з:

1) призначенням об'єкта;

2) станом об'єкта;

3) здатністю до дії;

4) впливом (застосуванням);

5) задоволенням потреб;

6) роллю;

7) обов’язком.

34. Зв’язок – це взаємообумовленість існування явищ, розділених у просторі і часі. Функціональний зв’язок встановлює взаємну обумовленість функцій одного об'єкта від реалізації функції іншого об'єкта.

35. Розрізняють системи:

1) механічні та робото-технічні;

2) біологічні – рослинний та тваринний світ;

3) соціологічні – спільнота людей.

36. У робототехнічних системах потрібні функції програмуються людиною, їх призначення – утримувати систему у стійкому стані для досягнення необхідних цілей.

37. У біологічних системах функції (функціональні перетворення) визначені генетичним кодом, проте зміни в навколишньому середовищі можуть ці функції модифікувати.

38. У соціологічних системах людина, що є елементом цілеспрямованої системи, може здійснювати одну і ту ж функцію різними способами. Число способів здійснення функції обмежено тими цілями, яким слугують функції.

39. Форма є зовнішньо загальним виглядом об'єкта безвідносно до його сутності (без урахування устрою його частин).

40. . Структура є множина частин чи форм, які знаходяться у взаємодії у специфічному порядку для здійснення функції

41. Сукупність – це з'єднання чи набір частковостей у єдину множину чи у суму безвідносно до форми чи порядку.

42. Розрізняють такі типи потоків: енергетичні; матеріальні; інформаційні; фінансові; людські (кадрові).

43. Можливі чотири типи взаємодій структури і потоків:

1. структура змінюється природно чи штучно, а потоки залишаються на тому ж рівні;

2. потоки змінюються (природним чи штучним чином), а структура не змінюється;

3. зміна структури тягне за собою зміну потоків (якісні та/або кількісні);

4. зміна потоків тягне за собою зміну структури.

44. Входом системи називають усе, що „добувається” системою з навколишнього середовища для досягнення цілей системи. Це певні ресурси, що перетворюються в деякі кінцеві продукти в результаті процесів, що відбуваються в системі.

45. Виходом системи називають результат функціонування системи чи кінцевий стан процесів, що відбуваються в системі. Виходи системи визначають таким же чином, як дію системи на навколишнє середовище.

46. Процес (лат. пересунення), це:

1) послідовна система явищ, станів у розвитку чогось;

2) сукупність послідовних дій для досягнення якихось результатів

47. У будь-якій штучній системі існують три різні за своїм призначенням (роллю) підпроцеси: основний процес, зворотній зв’язок та обмеження

48. Основний процес перетворює вхід у вихід.

49. . Зворотній зв’язок виконує такі процедури:

1) порівнює вибірку виходу з моделлю виходу і виділяє відмінність;

2) оцінює зміст та сенс відмінності;

3) виробляє рішення, що відповідає відмінності;

4) формує процес введення рішення (втручання в основний процес системи) та діє на процес з метою зближення виходу та моделі виходу.

50. Обмеження визначаються (виробляються) споживачем результатів функціонування системи, що аналізує ці виходи. Обмеження системи складається з цілі (функції) системи та примусових зв’язків (якостей функції). Примусові зв'язки повинні бути сумісними з ціллю

51. За походженням – штучні, природні, змішані.

За характером зв’язку із зовнішнім середовищем – відкриті, закриті.

За складністю:

а) неживі

б) живі

52. Модель (лат. – міра, зразок) – це деякий об’єкт, який за певних умов замінює об’єкт, який є оригіналом, відтворюючи потрібні користувачеві властивості та характеристики оригінала, має за цих умов істотні переваги користуванн

53. Моделювання – це дослідження певних процесів, явищ чи систем (об'єктів) шляхом побудови та вивчення їх моделей; використання моделей для визначення чи уточнення характеристик та раціоналізації способів побудови знову створюваних об’єктів

54. За типами цілей розрізняють моделі:

• пізнавальні; прагматичні.

55.За тривалістю у часі розрізняють моделі:

• статичні; динамічні.

56.За засобами відтворення розрізняють моделі:

• ідеальні (абстрактні); матеріальні (реальні, речові).

57. Пізнавальні моделі є формою організації та подання знань, засобом з'єднання нових знань з наявними. Якщо у процесі створення пізнавальної моделі деякого реального об'єкта спостерігаються розходження, то здійснюється корекція моделі з метою наблизити її до реальності Прагматичні моделі є засобом управління практичними діями шляхом подання (представлення) потрібних дій, чи їх результату, тобто є робочим поданням цілі. Тому у випадку виявлення розбіжності між прагматичною моделлю та реальним об’єктом основні зусилля повинні бути спрямовані на корекцію (зміну) реальності. Прагматичні моделі носять нормативний характер, виконують роль стандарту, зразка, під який підганяються реальні об’єкти.

58.. Ідеальними називають моделі, побудовані засобами мислення, свідомості.

59. Інтуїтивні моделі будуються на вербальному (описовому) рівні. Ці моделі не встановлюють суворі кількісні співвідношення між явищами, що моделюються, обмежуючись лише аналізом якісних узагальнених понять, що відтворюють лише загальні тенденції розвитку явищ, напрямки змін властивостей об’єктів, що вивчаються, та ін. За способом подання семантичних моделей розрізняють: математичні, логічні, графічні моделі. Математичні моделі відіграють певну роль серед інших форм знакових моделей, проте їх важко чітко відокремити від логічних та графічних, внаслідок їх тісного переплетення

60. Аналітичні моделі передбачають реалізацію моделі у вигляді алгебраїчних, диференціальних та інших рівнянь, що пов’язують вихідні змінні з вхідними, доповненими системою обмежень. При цьому передбачається наявність однозначної обчислювальної процедури отримання точного розв'язку рівнянь

61. При алгоритмічному підході математична модель, що використовується, не припускає точного розв'язку і змушує звертатися до різних наближених, рекурентних методів, ітеративних процедур пошуку наближеного розв'язку. Це типовий підхід до створення моделей складних систем.

62. . Імітаційна модель являє собою певну обчислювальну процедуру, що описує об'єкт аналізу, його ознаки та дії (процеси), що викликають зміну ознак об'єктів, або появу та зникнення самих об'єктів. Імітаційна модель дає змогу з будь-якою заданою точністю параметрично відтворити систему довільної складності. Основними обмеженнями при створенні цих моделей є ресурси пам'яті і часу. Головним засобом реалізації імітаційних моделей є ЕОМ.

63. . Щоб матеріальна модель могла замінити оригінал у процесі цілеспрямованої діяльності, необхідно встановити відношення подібності між моделлю та оригіналом

64. Розрізняють три типи подібності: пряма (фізична); непряма; умовна. Цінність моделювання визначається в процесі виявлення відношень між оригіналом і моделлю

65. Основною властивістю будь-якої моделі є скінченність. Скінченність моделей визначається перш за все скінченністю наших ресурсних можливостей (енергетичних, матеріальних, часових). Крім того, модель є скінченою, оскільки вона відображає оригінал через скінчену сукупність його властивостей. Спрощеність моделей призводить до відмінності між моделлю та оригіналом, міру припустимої відмінності можна оцінити, якщо співвіднести її з метою моделювання. Тому для оцінки відповідності моделі та оригінала вводиться поняття “адекватність

66. Виділяють чотири рівні відношень (основних) між моделлю та оригіналом.

Перший рівень. До нього відносяться функціональні моделі, що відображають як зовнішні прояви діяльності, так і механізми регуляції.

Другий рівень утворюють поведінкові моделі, що відображають відношення “вхід – вихід” системи.

До третього рівня відносяться моделі, що виокремлюють з різноманітності “вхід – вихід” окремі взаємопов'язані характеристики.

На четвертому рівні розташовуються моделі, що виражають відношення деяких параметрів оригінала у формі функціональних (аналітичних, статичних) залежностей (наприклад, закон Ома, та ін.).

67. Функціональна модель типу “чорний ящик”, рис. 2.2.

Рис. 2.2. Формальна модель системи типу “чорний ящик”.

Вона містить такі компоненти: межі системи; входи системи; виходи системи; оточуюче (зовнішнє) середовище.

Ця модель є вихідною при побудові моделей складної системи і акцентує увагу дослідника на взаємодії системи із зовнішнім середовищем. Ця взаємодія здійснюється впливом цілей системи (цільового продукту) на зовнішнє середовище (іншу систему). Цільові продукти системи – це виходи системи. Зовнішнє середовище виявляє дію на систему через ресурсне забезпечення, яке дає змогу системі реалізувати свої цільові функції. Такі зв’язки зовнішнього середовища із системою називають входами системи. Сама система зображується у вигляді прямокутника („непрозорого ящика”), причому вміст („начинка”) цього ящика не розкривається, тому модель називається „чорним ящиком”. Увага звертається тільки на межі системи, які підкреслюють цілісність системи і відокремленість її від зовнішнього середовища. При побудові моделі дослідник відбирає з множини факторів системи тільки деяку їх кількість, яка включається до списку входів та виходів. Критерієм відбору слугує цільове призначення моделі, значущість того чи іншого зв’язку по відношенню до цілі. Ця модель є першим етапом моделювання, але й має важливе самостійне значення. Ще одна перспективна галузь її застосування пов’язана з дослідженням систем у їх природному стані, коли втручання у її функціонування неприпустимо, чи небажано. Цією моделлю доводиться обмежуватися з причини відсутності інформації про внутрішній устрій та стан системи, що аналізується

6 8. Розглядаючи систему як щось цілісне та уособлене від зовнішнього середовища, дослідник описує зовнішні властивості системи (по відношенню до зовнішнього середовища). Сама система, її внутрішній „устрій” є, як правило, неоднорідною, що робить необхідним розрізняти внутрішні частини, тобто структурувати систему. Рівень та глибина структуризації залежить як від самої системи, так і від цілей, що стоять перед дослідником. У системі розрізняють елементи (ЕЛ) і підсистеми різних рівнів. Підсистеми складаються з різного набору елементів (рис.)

Рис. 2.3. Формальна модель типу „склад системи”.

Побудова змістовної моделі системи на практиці є непростою задачею, її конкретний вигляд залежатиме від цілей моделювання, ступеня компетентності суб’єкта моделювання; рівня інформованості суб’єкта моделювання та спеціаліста-консультанта; необхідної глибини структуризації системи, що моделюється. Модель „склад системи“ повинна відповісти на питання про границі системи більш чітко, ніж модель „чорного ящика”, хоч це буває непросто.

69. Модель типу „структура схеми”

Реальне число зв’язків між будь-якими системами чи їх елементами є дуже великим, може вважатися нескінченним. Однак, при побудові пізнавальних і прагматичних моделей систем для досягнення потрібної мети використовуються ті зв’язки, вплив яких або можна оцінити, або наявність яких забезпечує потрібний рівень адекватності моделей. Тому розглядати модель “структура системи” безвідносно до сукупності елементів системи (модель „склад системи”) неправомірно. Тому ця модель будується після або разом з моделлю „склад системи”. Самостійну роль може відігравати етап вивчення різних структур, їх переваг і недоліків у контексті з елементарним складом системи.

Одна і та ж система може бути поданою різними структурами в залежності від стадії пізнання об’єкта чи процесу їх розгляду, цілей створення. У процесі дослідження чи проектування структура системи може змінюватися. Структурні моделі системи можуть бути засобом їх дослідження.

Рис. 2.4. Різноманітні типи структур: а) лінійна; б) дерево видна; в) матрична; г) мережна; д) кільцева.

70. Завершальною і найбільш повною моделлю системи є модель, що називається „структурною схемою системи”, яка представляє собою сукупність (з’єднання) трьох розглянутих раніше моделей: чорного ящика; складу та структури. У цій моделі описуються: всі елементи системи (склад); всі зв’язки системи: внутрішні (структура), зовнішні (входи, виходи); границі системи; параметри зовнішнього середовища; параметри внутрішнього середовища.

Основною проблемою побудови моделей складних систем є знаходження компромісу між простотою опису об’єкта та ступенем його деталізації. Один з шляхів розв’язку цієї проблеми – задавання системи сімейством моделей, кожна з яких описує поведінку системи з точки зору відповідного рівня абстрагування. Для кожного рівня існують характерні особливості, закони та принципи, за допомогою яких описується поведінка системи на цьому рівні. Таке уявлення називають стратифікованим, а рівні страгірування – стратами.

71. Поняття „динаміка системи” інтерпретується неоднозначно. Розрізняють три типи динаміки системи: функціонування, ріст, розвиток. Під функціонуванням розуміють процеси, які відбуваються в системі для того, щоб система реалізовувала свою ціль. Під ростом системи розуміють таке її функціонування, коли відбуваються якісні зміни деяких характеристик системи, що реалізують ті ж функції для досягнення тієї ж цілі (або цілей).

72. У самому загальному вигляді динамічну модель можна описати так: вводять поняття „стан системи” як деякої „внутрішньої” характеристики системи. Зазвичай стан системи характеризується набором величин z₁(t),…, z_n(t), які утворюють вектор , який є функцією часу. Вектор входу системи та вектор виходу системи також є функціями часу. У простому випадку вектори входу , виходу та стану пов’язані між собою співвідношенням , де f – деяка функція. Тобто динамічна модель системи – це сукупність співвідношень, що визначають вихід системи в залежності від входу та стану системи

73. Моделі складних систем базуються на: математичному аналізі; теорії імовірності; математичній статистиці; теорії надійності та ефективності, теорії ігор, ТМО, теорії корисності та розпізнавання образів, теорії інформації, теорії управління, теорії оптимізації, та ін.

74. Задача ідентифікації формулюється наступним чином: за результатами спостережень за входами та виходами системи, побудувати оптимальну (у смислі певного критерію) модель; вважається, що система знаходиться у формальному режимі функціонування, тобто за обставин випадкових збурень та завад.

75. Адекватністю називають властивість моделі, яка полягає у можливості відтворення нею з необхідною повнотою тих властивостей якості об’єкта, які є істотними для цілей даного дослідження. Вимога адекватності моделі та об’єкта – це необхідна умова для переходу від дослідження об’єкта до дослідження моделі та подальшого перенесення результатів з моделі на об’єкт досліджень

76. Система називається детермінованою, якщо результат спостереження над нею, за умови багаторазового повторення експерименту за незмінних умов, є одним і тим же (однозначним). Будь-якому реальному процесу притаманні випадкові флуктуації, проте вибір детермінованої чи імовірнісної математичної моделі є справою вибору дослідника, що визначається наявністю чи відсутністю намірів враховувати випадкові фактори

77. Аналітичні моделі характеризуються тим, що процеси функціонування елементів складної системи можна подати у вигляді певних функціональних співвідношень ( алгебраїчних, диференціальних, інтегральних, інтегрально-диференціальних, скінченно-різницевих, логіко-алгебраїчних, та ін. Аналітична модель досліджується: аналітично (шляхом отримання явних залежностей для величин, які слід визначити); чисельно (шляхом отримання числових результатів за умови конкретних початкових даних); якісно (шляхом знаходження певних властивостей розв’язку, зокрема оцінки стійкості розв’язку).

78. Останнім часом набуло поширення комп’ютерне моделювання процесів. В цьому випадку замість аналітичної моделі досліджуваного процесу використовується алгоритмічний опис процесу її функціонування з використанням алгоритму, призначеного для реалізації на комп’ютері. Проте найбільш повний і вичерпний опис можна отримати тоді, коли отримані явні залежності, які пов’язують невідомі величини, які слід визначити, з параметрами системи та початковими умовами. Як правило, їх можна отримати лише для простих систем. Якщо ж система є достатньо складною, то аналітичний розв’язок наштовхується на значні, під час непереборні, складнощі. В цьому випадку, намагаючись отримати аналітичний розв’язок, йдуть на зумисне спрощення початкової моделі, задля того, щоб мати можливість вивчити деякі загальні властивості системи

79. Для отримання аналітичних розв’язків використовують потужні математичні методи. Якщо ж досліджувана система є достатньо складною, то задля отримання аналітичного розв’язку на модель накладаються жорсткі обмеження, вдаються до спрощень. Часто доводиться нехтувати деякими особливостями системи, від чого створена модель перестає відповідати своєму основному призначенню – бути засобом вивчення складної системи, яка вивчається. Проте все ж намагаються розробляти таку математичну модель, яка забезпечує хоч і грубий, але простий, доступний для огляду, розв’язок задачі, що розглядається. Цей розв’язок використовується для отримання точніших розв’язків іншими методами.

Чисельні методи, у порівнянні х аналітичними, можна застосувати до більш широкого кола функціональних рівнянь, проте отримані розв’язки мають частковий характер, вони не дають змоги отримати висновки загального типу. Ефективність використання цих методів останнім часом зростає в зв’язку з впровадженням сучасної комп’ютерної техніки як в задачах розрахункового типу, так і в задачах управління та моделювання структури складних систем

80. Диференціальні рівняння використовується для моделювання систем та явищ різної природи: механічні, електричні, економічні, та ін. Так, наприклад, малі коливання маятника, рис. 3.1, описуються диференціальним рівнянням

81. При моделюванні процесів автоматичного управління дотримуються схеми, рис.3, за якою реальний об’єкт складається з двох підсистем, які взаємодіють: керованої та керуючої.

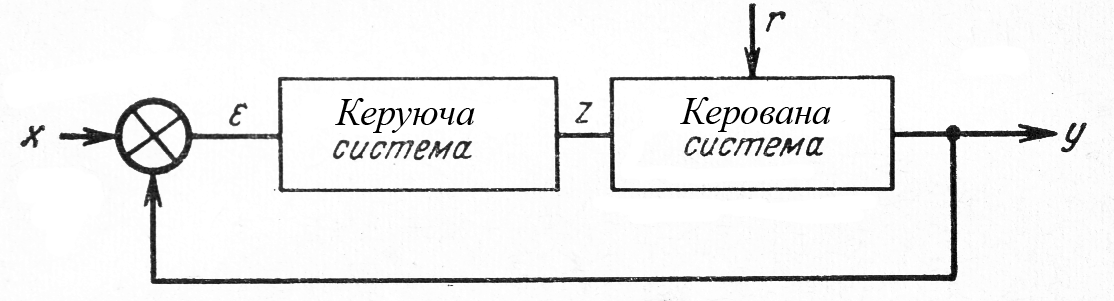
Рис. 3.3. Схема автоматичного управління за однією координатою стану системи

На рис.3.3 y(t) – координата стану системи, x(t) – дія завдання,(t) – сигнал похибки, z(t) – керуюча уюча дія z(t), яка виробляється системою керування, є функцією похибки Функція формується таким чином, щоб виконувалася наближена рівність За реальних умов до системи, окрім збурення , яке задається і несе в собі інформацію, необхідну для управління, надходить збурення , яке не містить корисної інформації. Збурюючі дії порушують потрібний функціональний зв’язок між дією, яка задається, та законом зміни вихідної координати. Вони можуть сильно спотворювати корисну інформацію і зробити систему непрацездатною.

82. На рис. 3.3 наведено схему автоматичного управління за однією координатою стану системи, в загальному ж випадку управління може здійснюватися за кількома координатами, рис. 3.4:

Рис.3.4. Схема автоматичного управління за кількома координатами стану системи

Дослідження багатовимірних систем є складнішою обчислювальною задачею, проте відповідна методика не залежить від числа координат стану системи. Керованою системою (об’єктом) може бути окремий двигун, ядерний реактор, цех заводу, завод у цілому, тощо, тобто це – сукупність технічних засобів, які забезпечують виконання керованою системою певної цілі. Точність виконання керованою системою заданої цілі визначається тим, наскільки точно відтворюється координата стану системи у(t), різниця між заданим у_з(t) та дійсним у(t) значеннями величин, які визначають управління, є похибкою управлінн

84. Системи, для яких похибки управління дорівнюють нулю в будь-який момент часу, називаються ідеальними. Практичне здійснення ідеальних систем управління неможливе внаслідок того, що похибка є важливим елементом управління, що базується на принципі від’ємного зворотного зв’язку (для приведення у відповідність вихідної величини до її заданого або бажаного значення використовується інформація про відхилення між ними). Задачею системи автоматичного управління є зміна величини у(t) у відповідності до заданого закону з певною точністю. В процесі проектування систем автоматичного управління необхідно вибирати такі параметри системи, які б забезпечували необхідну точність управління. Окрім цього, параметри системи повинні забезпечувати вимоги стійкості та регулярності поведінки системи в перехідному процесі

88. . Стаціонарні системи описуються диференціальними рівняннями із сталими коефіцієнтами. Якщо система є нестаціонарною, то коефіцієнти відповідних рівнянь є функціями часу. Така класифікація систем автоматичного управління за способом їх математичного опису є умовною

89. Нехай система автоматичного управління описується системою диференціальних рівнянь:

90. Теорія стійкості вивчає вплив збурюючи факторів на поведінку (рух) досліджуваної системи. Збурюючими факторами є сили, які не враховуються при опису руху внаслідок їх малої величини, порівняно з основними силами. Вони можуть діяти миттєво, що призводить до малої зміни початкового стану системи, або неперервно. Це означає, що складені диференціальні рівняння руху відрізнятимуться від істинних, що в них не враховані певні малі поправочні коефіцієнти. Вплив малих збурюючи факторів на рух системи буде різним, на одні рухи цей вплив незначний, коли збурений рух мало відрізнятиметься від незбуреного; на інші – значний, коли збурений рух значно відрізняється від незбуреного і матиме місце нестійкий рух.

91. За Ляпуновим, розв’язок y^*_i(t), i = 1, 2, …, n системи типу (3.21) називаються стійкими, якщо, за умови будь-якої заданої області припустимих відхилень від стану рівноваги, можна підібрати область припустимих початкових умов , яка має ту властивість, що жодний рух, який починається всередині , ніколи не досягне границь області .

92. Близькі за початковими умовами розв’язки залишаються близькими для всіх t ≥ t₀. Розв’язок системи (3.21) називається стійким, якщо існує область припустимих відхилень від стану рівноваги, для якої не існує область , яка є околом стану рівноваги і має ту властивість, що жодний рух, який розпочинається всередині , ніколи не досягне границі області , або якщо цей розв’язок не продовжуваний при t →∞.

93. Якщо стійкий розв’язок при задовольняє умову

(3.24)

для всякого розв’язку то в цьому випадку має місце асимптотична стійкість.

94. Стійкість за Ляпуновим – це стійкість для достатньо малих початкових відхилень, вона, як поняття, є важливою тоді, коли досліджується чисто фізична здійснюваність певного стану рівноваги. Якщо стан рівноваги є стійким за Ляпуновим, то він фізично здійсненний, якщо ж ні, - то нездійсненним, оскільки за будь-яких, як завгодно малих початкових відхиленнях зображуючи точка системи розпочне відхід з околу точки рівноваги.

95. Теорема 1. (без доведення)

Стан рівноваги x₀ = 0 диференціального рівняння

є асимптотично стійким, якщо стан рівноваги 0, який відповідає вільній лінійній стаціонарній системі

де А =є асимптотично стійким.

Аналогічно стійкості рівноваги визначається стійкості руху за Ляпунову.

Теорема 2. (без доведення)

Стан рівноваги 0 диференціального рівняння

є нестійким, якщо стан рівноваги 0 відповідної лінійної стаціонарної системи

,

де А = є асимптотично стійким.

96. Цей метод дає змогу дослідити стійкість системи, не розв’язуючи диференціальні рівняння стану. Стійкість досліджується з використанням властивостей відповідних функцій, які називаються функціями Ляпунова.

Якщо існує диференційована функція , яка називається функцією Ляпунова, яка задовольняє в околі початку координат такі умови:

1. причому при

2. при внаслідок (1.21), то точка спокою системи є стійкою.

Існування функції Ляпунова гарантує стійкість, це можна пояснити наступним чином. Слід відмітити, що рух у фазовій площині здійснюється проти часової стрілки. Система стійка, якщо для будь-якого існує таке, що за умови виконується нерівність для всіх .

97. Дискретні пристрої в сучасній техніці займають значне місце, це – обчислювальні та керуючі машини дискретної дії, керуючі системи автоматичної телефонії, тощо. Найпростішим елементом дискретної системи є реле – елемент, вхідна та вихідна величини якого можуть приймати лише скінченне (два, три) число значень. Реле може бути виконано на діодах, тріодах, електронних лампах.

Всі релейні пристрої поділяються на два класи: однотактні та багатоактні. Однотактні пристрої – це пристрої без пам’яті, в яких сукупність вихідних сигналів в будь-який момент часу представляють собою однозначну функцію вхідних сигналів в той же момент часу. Багатотактні пристрої – це релейні пристрої з пам’яттю, в яких сукупність вихідних сигналів в будь-який момент часу залежить не тільки від сукупності вхідних сигналів, але й від внутрішнього стану пристрою.

98. Функції f(x₁, x₂,…,x_n) від будь-якого скінченного числа булевих змінних, які приймають значення 0 чи 1, називаються мулевими функціями. Існує різних булевих функцій від n змінних, включно з функціями меншого числа

99. У випадку однієї змінної існує всього чотири мулевих функції: функції-константи функції повторення функції заперечення (інверсія) (не «х»), рівна одиниці, коли х =0, і рівна нулеві, коли х=1. Число мулевих функцій від двох змінних становить 16, включно з функціями-константами функції повторення

100. Багатоконтактні пристрої доцільно досліджувати на їх спільній моделі, зображеній на рис. 3.9. За термінологією Хафмена-Мура – це є послідовнісна перемикаюча схема.

Спільна модель багатоконтактного пристрою характеризується трьома множинами: вхідним алфавітом , вихідним Y = { та множиною внутрішніх станів В даному такті вихідні сигнали моделі є функцією всіх вихідних сигналів та всіх внутрішніх станів в цьому такті:

101. Скінчений автомат характеризується трьома множинами: вхідним алфавітом Х, вихідним Y та множиною внутрішніх станів Z. Ці множини є скінченними, якщо на вхід автомата надходить слово р з вхідного алфавіту Х, то на виході з’являється слово g з алфавіту Y, причому вихід автомата залежить не тільки від входу, але й від внутрішнього стану.

102. Введем о поняття автоматного часу, який дорівнює нулеві на початку роботи скінченого автомата і збільшується на одиницю за умови надходження на вхід автомата кожного наступного сигналу. Послідовні моменти часу надходження чергового сигналу ототожнюють з послідовним рядом натуральних чисел t = 0, 1, 2, … Ці числа називають тактами

103. Функціонування скінченного автомата описується двома функціями: функцією переходів δ (до нового стану) та функцією виходів λ:

(3.43)

(3.44)

В цих виразах - поточний такт; - вхідний сигнал;- стан, до якого переходить автомат в поточному такті; - стан, в якому автомат знаходився до надходження вхідного сигналу ; - вихідний сигнал, який виробляється автоматом в такті.