ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Методичка
Дисциплина: Системы искусственного интеллекта
Добавлен: 29.10.2018
Просмотров: 394
Скачиваний: 7
ЛАБОРАТОРНАЯ РАБОТА № 2.
ТЕМА:РАССУЖДЕНИЯ В ПРОСТРАНСТВЕ СОСТОЯНИЯ СРЕДЫ.
Искусственный интеллект занимается созданием интеллектуальных сущностей, объектов, которые принято называть агентами или носителями.
Агент воспринимает внешнюю среду с помощью датчиков x 1,x2 ,….,x m и воздействует на нее посредством исполнительных органов z1,z2,….,zn, подобно тому, как человек воспринимает внешнюю среду или просто среду с помощью органов чувств и воздействует на нее с помощью таких частей тела, как руки, ноги и т.п.
Предполагается, что создание агента любого типа осуществляется человеком, и он всегда способен решать задачи суперагента любого уровня. Процесс создания агента сам по себе неформален и качество описания, выражающееся в степени адекватности поведения получаемого агента задуманному, зависит от учета создателем всех необходимых аспектов его будущего поведения. Иначе говоря, создатель агента должен включить в его описание все правила, необходимые для задуманного поведения. Совокупность всех таких правил называют иногда базой знаний агента.
Эту базу знаний можно представить в некотором формальном языке, в частности, языке логики.
В ответ на свое восприятие агент с помощью логических рассуждений на основе знаний, хранящихся в базе знаний, способен вырабатывать реакции. Механизм рассуждений зависит от типа агента и от языка представления базы знаний.
Логические рассуждения.
Рассуждением или умозаключением обычно называют ряд мыслей, изложенных в логически последовательной форме.
Агент должен уметь находить интересующие его состояния среды (целевые состояния), если он что-либо знает о других ее состояниях. Определение целевых состояний осуществляется с помощью поиска или рассуждений в пространстве состояний.
В коммунальной квартире две старушки занимают по комнате. Комнаты находятся в общем коридоре, который имеет выход на лестничную клетку. Одна из комнат расположена слева (левая комната) от выхода, а другая — справа (правая комната). В коридоре живет кот, которого обе старушки одинаково любят и балуют, оставляя ему кусочки сыра. Каждая старушка кладет кусочек сыра у двери своей комнаты. Кот отдыхает либо у левой комнаты (слева), либо у правой (справа).
Множество всех состояний этой среды (среды кота) можно представить табл.1, в столбцах которой для каждого состояния среды указаны - местонахождение кота (слева или справа), наличие или отсутствие кусочка сыра (да или нет) у соответствующей комнаты.
Состояние b1 означает, что кот находится около левой комнаты и около обеих комнат лежит по кусочку сыра, состояние b2 - кот находится около правой комнаты и около обеих комнат снова лежит по кусочку сыра и т.д
Таблица 1
-
Состояние
Местонахождение кота
Наличие сыра
слева
справа
b1
Слева
Да
Да
b2
Справа
Да
Да
b3
Слева
Да
Нет
b4
Справа
Да
Нет
b5
Слева
Нет
Да
b6
Справа
Нет
Да
b7
Слева
Нет
Нет
b8
Справа
Нет
Нет
Кот может совершать в один и тот же момент времени только одно из следующих действий: переходить к дверям левой комнаты, переходить к дверям правой комнаты и съедать кусочек сыра около той комнаты, где он находится. Эти действия обозначим с1 = Идти налево, с2 = Идти направо и с3 = Съесть, соответственно. Если среда находится в одном из состояний, перечисленных в табл. 1, и кот совершает какое-либо из действий, то нетрудно определить в какое состояние после выполнения действия перейдет среда.
Будем полагать, что нам известно состояние, называемое начальным, с которого могут начаться изменения среды при действиях кота.
Пусть, например это будет состояние b1. Будем изображать состояния кружочками с обозначением состояния внутри кружочка. Переход из одного состояния в другое,
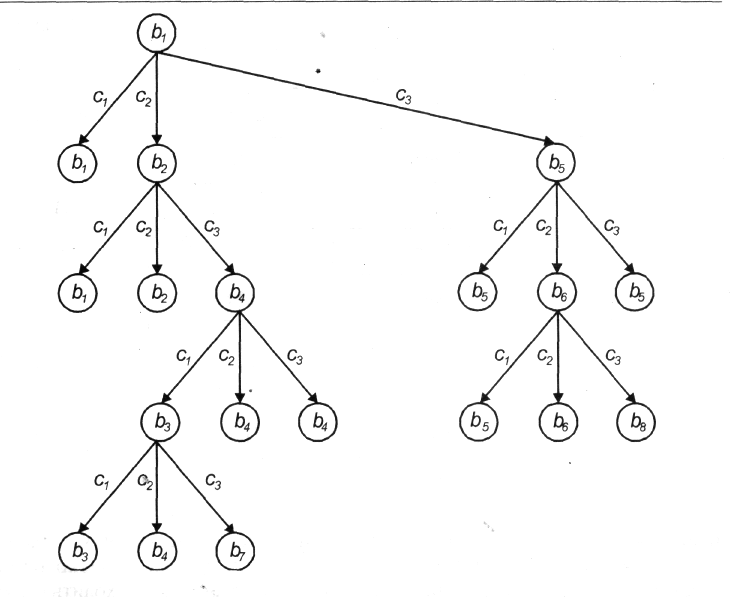
Рис.1 Дерево переходов.
происходящий в результате действия, будем изображать стрелкой, ведущей в это другое состояние и помеченной соответствующим действием. На рис. 1 показано дерево всех дальнейших переходов. Построение каждой ветви дерева прекращено на том состоянии, которое встречается повторно на пути, ведущем в него из начального состояния.
Цель кота - не оставить ни одного кусочка сыра, где бы он изначально ни находился. В терминах состояний среды целью кота является перевод ее с помощью своих действий (реакций) в одно из состояний b7 или b8 . Состояния, в которые с помощью набора допустимых действий необходимо перевести среду, называются целевыми. Процесс определения этих состояний называют формулировкой цели. Будем полагать в рамках нашего примера, что каждое восприятие совпадает с одним из состояний. Задачей агента является нахождение последовательности действий или пар восприятие-действие, ведущих на дереве переходов из начального состояния в целевые. Процесс нахождения этих последовательностей называют поиском, выводом или рассуждением. Постановкой задачи называют задание всех состояний и действий, которые можно использовать для решения задачи, начального состояния и целевых состояний, а также всех допустимых переходов между состояниями при выполнении действий. Для среды кота постановка задачи уже осуществлена. Все состояния, которые могут использоваться при решении задачи, перечислены в табл. 1. Целевыми состояниями являются состояния b7, b8. Все допустимые переходы между состояниями показаны на рис.1 Из рисунка ясно, что решениями задачи является последовательность b1/c2, b2/c3,b4/c1,b3/c3, в результате выполнения которой агент (кот) переведет среду в состояние b7, и последовательность b1/c3, b5/c2, b6/c3, в результате выполнения которой среда окажется в состоянии b8. В таблице 2 приведены все последовательности исходных состояний, действий и соответствующие им переходы в новое состояние.
Таблица 2
|
Переход |
||
|
Исходное состояние |
Действие |
Результирующее состояние |
|
b1 |
c1 |
b1 |
|
b1 |
c 2 |
b2 |
|
b1 |
c3 |
b5 |
|
b2 |
c1 |
b1 |
|
b2 |
c2 |
b2 |
|
b2 |
c3 |
b4 |
|
b3 |
c1 |
b3 |
|
b3 |
c2 |
b4 |
|
b3 |
c3 |
b7 |
|
b4 |
c1 |
b3 |
|
b4 |
c2 |
b4 |
|
b4 |
c3 |
b4 |
|
b5 |
c1 |
b5 |
|
b5 |
c2 |
b6 |
|
b5 |
c3 |
b5 |
|
b6 |
c1 |
b5 |
|
b6 |
c2 |
b6 |
|
b6 |
c3 |
b8 |
Решения задачи для среды кота практически очевидны, когда построено дерево переходов состояний среды, по которому легко проследить пути, ведущие в целевые состояния из начального. В реальных задачах это дерево может быть очень большим, вследствие чего нецелесообразно использовать стратегию поиска, согласно которой необходимо сначала получать дерево целиком. Вместо этого используются другие более эффективные стратегии поиска.
Однако, какая бы из этих стратегий не применялась, элементарным шагом поиска является переход из одного состояния среды в другое и анализ состояния, в которое переход был осуществлен, на принадлежность к числу целевых. Каждый допустимый переход из состояния bi. после совершения действия сj в состояние bk можно задавать с помощью правила перехода: «Если среда находится в состоянии bi. и совершается действие сj, то она должна перейти в состояние bk».
Совокупность правил подобного типа используется в процессе поиска. Одной из очевидных, но чрезвычайно неэкономных стратегий поиска, позволяющей найти все решения для среды кота, может быть следующая.
1. Образовать множество В = {b1}, состоящее из одного начального состояния b1.
2. Для каждого состояния множества В и каждого действия с найти, согласно соответствующим правилам перехода, все состояния bk, в которые переходит среда. Совокупность всех таких состояний, за исключением тех, которые уже встречались в ранее образованных множествах В, принять за новое множество В.
3. Проверить, нет ли среди элементов этого множества целевых состояний. Если целевых состояний нет, то перейти к п. 2. Если целевые состояния есть, то выписать в порядке использования правил все последовательности действий, которые привели к целевым состояниям, удалить эти состояния из множества В и перейти к выполнению следующего пункта.
4. Проверить, все ли целевые состояния найдены. Если найдены все, то прекратить поиск. Если найдены не все, то перейти к п. 2.
В соответствии с этими правилами и таблицей 2 была составлена МАТКАД – ПРОГРАММА решения задачи. Программа начинается словом ORIGIN=1. Это означает, что нумерация всех элементов будет начинаться с единицы, а не с нуля.
В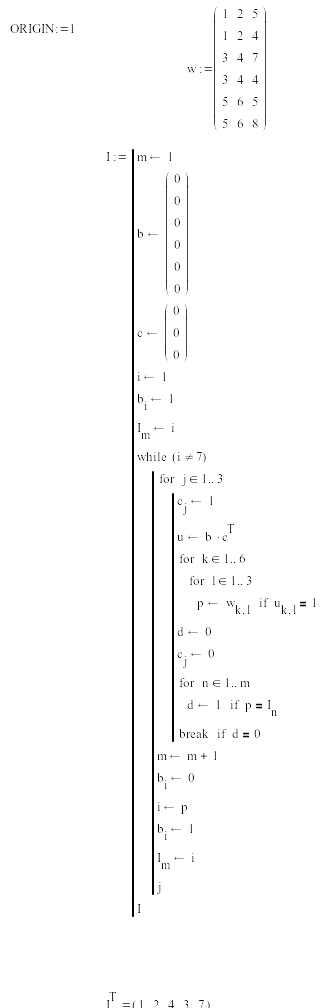
допрограммной части размещена матрица
w , в которой номера
переходов при том или ином действии.
Например, при исходном состоянии b1
и действии c1
агент переходит в состояние b1.
Элемент матрицы w11
равен 1. При исходном состоянии b4
и действии c1 агент
переходит в состояние b3.
Элемент матрицы w41
равен 3 и т.д.
В доцикловой части самой программы дается размерность векторов b и c , задается начальное значение i=1 и значение bi=1.
Формируется первый элемент вектора I, в котором будут помещены все индексы переходных состояний.
После этого формируется цикл while до одного из конечных состояний i=7. Внутри этого цикла формируется цикл for j=1..3 для просмотра всех трех возможных действий и матрица u=b*ct
В развернутой форме эта матрица имеет вид:
.
Далее в двух вложенных циклах происходит сравнение всех элементов матрицы u с единицей, и в случае этого равенства
Вспомогательной величине p присваивается значение соответствующего элемента матрицы w. На первом цикле u11=1, поэтому p=w11 =1. Следующий цикл for n=1 to m проверяет, не встречалось ли раньше вновь наступившее состояние. Если оно не встречалось, то цикл по действию с прекращается, компьютер начинает исследовать возможные действия из вновь наступившего состояния.
Рассмотрим несколько шагов выполнения программы. В начале происходит присвоение m=1. Это значит, что в векторе последовательности состояний I первое состояние – b 1 . До циклов присваивается i=1 ( начальное состояние – b1 ).
Компьютер входит в цикл while и затем в цикл for j. Выбирается действие с1 и вычисляется матрица u. Т.к. b1 и с1 равны 1, то первый элемент этой матрицы u11 =1 а все остальные ее элементы равны нулю, так как равен нулю хотя бы один из сомножителей.
Во вложенных циклах for k и for l происходит присвоение 1 новому состоянию , которое заносится в вспомогательную величину р. Далее в цикле for n новое состояние р=1 сравнивается с предыдущим, которое также равно 1. Программно это обозначается значением переменной d. На этом шаге d=1, поэтому компьютер возвращается в начало цикла for j, присваивает j=2, отсюда сj=2 также. В матрице u u12=1, а все остальные элементы равны нулю, поэтому p=w12, т.е. p=2. Компьютер переходит на цикл for n. Так как p=2, а I1=1, то d=0 и по команде break компьютер выходит из цикла for j.
После этого цикла новое состояние ( 2) передается в i и в вектор I заносится элемент I2. Так как i не равно 7, машина приступает к новому циклу по while. Снова выбирается действие с1, переменной р присваивается значение w21 =1, так как только u21=1. Так как I1=1 и р=1, компьютер переходит к действию с2, теперь u22=1, w22=2. Так как состояние 2 уже было происходит переход к действию с3 , после которого агент переходит в состояние 4. Из этого состояния после попытки действий с1 и с2 он переходит путем действия с3 в конечное состояние 7. Задача решена.
Ответ приведен в виде транспонированного вектора I.
ЗАДАНИЕ: Набрать программу, получить решение.