Файл: Лекция 1. Графический способ обработки опытных данных.doc

Скачать файл (0,39Мб)

Заказать решение

ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса

Категория: Лекция

Дисциплина: Методы обработки экспериментальных данных

Добавлен: 29.10.2018

Просмотров: 387

Скачиваний: 13

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ВВЕДЕНИЕ

Для решения задач, связанных с обработкой экспериментальных данных при наличии случайных и непредсказуемых воздействий за последние двести лет был выработан мощный и гибкий арсенал методов, называемых в совокупности математической статистикой (а также прикладной статистикой или анализом данных). Эти методы позволяют выявлять закономерности на фоне случайностей, делать обоснованные выводы и прогнозы, давать оценки вероятностей их выполнения или невыполнения. Статистика – это инструментарий, помогающий эффективно разбираться в сложном экспериментальном материале.

Целью данного пособия является формирование у студентов представления об основных статистических процедурах и способах их применения; умение самостоятельно проводить первоначальную статистическую обработку данных экспериментальных исследований; умение делать правильные выводы на основе результатов статистического анализа.

Данное пособие содержит теоретические сведения о теории корреляции, методе наименьших квадратов, графическом методе представления информации, дисперсионном анализе, об ошибках измерений.

Современные приложения дисперсионного анализа охватывают широкий круг задач экономики, социологии, биологии и техники и трактуются обычно в терминах статистической теории выявления систематических различий между результатами непосредственных измерений, выполненных при тех или иных меняющихся условиях.

1. Графический способ обработки опытных данных

Пусть опытные данные представлены таблицей. Через точки, определяемые этой таблицей или близкие к ним, проводят график и по виду графика подбирают вид эмпирической формулы. Простейшим случаем считается тот, для которого данные опыта приводят к точкам, располагающимся приблизительно на прямой или на кривых, уравнения которых и преобразуют заменой переменных к линейной функции. Решив эту задачу графическим способом, наносят точки на координатную сетку (с равномерной или логарифмической шкалой) и проводят прямую приблизительно через эти точки так, чтобы она проходила возможно ближе к каждой из нанесенных точек, а затем берут две произвольные точки на этой прямой (возможно дальше одна от другой) и подставляют их координаты в соотношение . Из полученных таким образом двух уравнений находят значения и .

Пример: Стационарное распределение температуры в теплоизолированном тонком стержне описывается линейной функцией . Определить постоянные и , если дана таблица измеренных температур в соответствующих точках стержня:

x	0	2	6	8	10	14	16	20
u	32	29,2	23,3	19,9	17,2	11,3	7,8	2

Построив точки, отвечающие данной таблице, видим, что прямая проходит через точки (0;32) и (20;2). Подставляя их координаты в уравнение , приходим к системе

Отсюда получаем искомое соотношение .

Насколько хорошо полученная формула отвечает табличным данным, можно судить по величине суммы уклонений и суммы квадратов уклонений значений функции, вычисленных с помощью этой формулы, от табличных значений. В данном примере имеем . Следовательно,

; ;

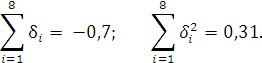
Пример: Табличные данные

t	1	2	3	4	5	6	7
S	2,31	2,58	2,77	2,93	3,06	3,16	3,26

отвечают формуле . Найти значения А и

Логарифмируя равенство , получим полагая , имеем +. Графиком полученного линейного уравнения служит прямая, параметры уравнения которой найдем, взяв две точки на этой прямой, например (и (.