Добавлен: 29.10.2018
Просмотров: 5504
Скачиваний: 25
Среди простых суждений по качественной характеристике связки-отношения можно выделить суждения действительности (ассерторические), необходимости (аподиктические) и возможности (проблематические). В целом всю эту группу суждений называют суждениями модальности. Модальность — это, можно сказать, степень достоверности содержания того или иного простого суждения, что в логической форме выражается связкой и другими логическими операторами.
Суждения действительности — те, которые адекватно или неадекватно, но все равно категорично (что и выражается связками «есть», «не есть», «суть», «не суть» и др.) отражают настоящее.
Суждения необходимости могут отражать прошлое, настоящее и будущее. Они выражаются оператором «необходимо», включенным в структуру суждения: «Необходимо, что S есть Р», «Необходимо, что кислород способствует горению», или «Кислород необходимо способствует горению», «Необходимо, что сумма внутренних углов треугольника на плоскости равна двум прямым» и т.п.
Суждения возможности тоже отражают то, что могло быть в прошлом, может быть в настоящем или в будущем. Они выражаются с помощью оператора «возможно», «вероятно» и пр.: «Возможно, что S есть Р», «Вероятно, что завтра будет дождь», «Возможно, что он был обманут». Истинностные зависимости между модальными суждениями будут рассмотрены позже.
Особую группу составляют суждения существования (экзистенциальные суждения), утверждающие существование того или иного предмета (явления, процесса): "Жизнь существует", "Солнце есть" и т.п. Связка и предикат этих суждениях как бы сливаются (отождествляются или подразумеваются). Чисто внешне кажется, что они представляют собой неполное простое категорическое суждение, только его часть: «S есть», «S—». Наличие суждений существования позволяет выдвинуть положение о сокращенной записи простых суждений, например, «Солнце существует», восстановление которых дает полное суждение «Солнце есть существующее».
Поскольку в любом суждении логические связи устанавливают отношения между крайними, составляющими эту структуру, элементами, постольку всякое суждение может считаться суждением отношения. В более строгом, узком значении слова в логике суждениями отношения называют те, в которых устанавливаются отношения причины и следствия, части и целого, пространственные, временные и другие, выразимые в языке словами (операторами): больше, меньше, старше, правее, выше, южнее и т.п., например, "5 больше 3", "Нева полноводнее Дона", "Отец старше сына". Символически суждения отношения выражаются формулой "в R с", где символы в (предшествующий член отношения) и с (последующий) соответствуют отдельным понятиям, а символ R - отношению между ними. Читается формула: "в и с находятся в отношении R", или "в находится в отношении R к с".
Свойства, зависимости и особенности этих отношений — предмет современной формальной (математической) логики, вооруженной специальными средствами исследования (математическими методами, исчислениями), помогающими рассмотреть многообразие зависимостей и связей, следствий этих отношений. Традиционная логика, не обладая такими средствами, необходимо сужает, по сравнению с современной, предмет своего исследования, ей не под силу детальное рассмотрение многообразных модальных отношений, тоже требующих для своего исследования сложного научного аппарата. Наиболее же общие закономерные свойства, исследуемые логикой в отношениях, есть симметричность (коммутативность), когда в=с и, соответственно, с=в; когда в+с=с+в, или когда в х с равно с х в; асимметричность, когда в>c, но, соответственно, с<в; переходность (транзитивность), когда в>с, а с>d, то и в>d; рефлексивность, когда при в=с, в=в, а с=с и т.п.
Есть еще так называемые выделяющие простые категорические суждения, отражающие принадлежность (или нет) чего-то только данному предмету (группе их): "Только равноугольные треугольники равносторонни", "Только человек мыслит", "Дорогу осилит только идущий" и т.п.
В традиционной формальной логике основное внимание уделяется, как правило, рассмотрению простых категорических суждений, и лишь некоторых сложных, в большей степени, условных и разделительных, в меньшей - соединительных и эквивалентности.
§ 2. ОПРЕДЕЛЕНИЕ ПРОСТОГО КАТЕГОРИЧЕСКОГО СУЖДЕНИЯ,
ЕГО СТРУКТУРА И ВИДЫ
Опираясь на уже известное определение простого суждения, категорическое суждение (суждение действительности) можно определить как такое, в котором что-то утверждается или отрицается относительно предмета мысли. Другими словами — это такое простое суждение, в котором между субъектом и предикатом устанавливается категорическая (утвердительная или отрицательная) связь, т.е. отношение тождества, подчинения, частичного совпадения, противоречия, противоположности и соподчинения: "Жучка есть собака», «Студент не есть профессор» и т.п.
Как и любое суждение, простое категорическое суждение может быть истинным («и») или ложным («л»). В языке это суждение выражается повествовательным предложением, при этом тесная связь и взаимозависимость суждения и предложения не является основанием для их отождествления.
Структура простого категорического суждения обычно представляется трехэлементной, т.е. такое суждение состоит из субъекта, предиката и связки, что удобно представить в виде формулы: S--P. Но здесь непроизвольно опускается тот элемент, который связан с количественной характеристикой субъекта суждения, т.е. квантор. C учетом его приходится говорить о четырех элементах простого категорического суждения. Символическое изображение такого суждения уже приводилось. Логическая связь (утверждение или отрицание), т.е. связка между субъектом и предикатом простого категорического суждения выступает основным структурным законом, необходимой связью элементов, формирующих целостность данной форму мысли.
Простые категорические суждения по количественному и качественному признакам подразделяются на виды. По количественному (объемному) показателю, выражаемому квантором, простые категорические суждения делятся на единичные, частные и общие.
Единичное суждение отражает единственный предмет мысли, т.е. субъект этого суждения — единичное понятие: «Крупнейший город Северо-Запада нашей страны расположен в устье Невы».
Частное суждение отражает некоторую совокупность предметов, но не всю, что и подчеркивается квантором: «Некоторые S есть Р», «Многие студенты — отличники», «Встречаются такие S, которые есть Р». При более обстоятельном рассмотрении квантора существования выявляется, что в количественном отношении частные суждения все-таки весьма неопределенны. Так, выражение «Некоторые S...» допускает несколько значений: «Некоторые, а может быть, большинство, а может быть все...», «Некоторые, а может быть, один...», «Некоторые и только некоторые...». Преодоление количественной неопределенности частных суждений требует хорошего знания той предметной области, которую они отражают. Одного логического знания в таких случаях недостаточно, особенно когда решается вопрос об истинности суждений, об отношениях между суждениями, где точность количественной характеристики частного суждения весьма существенна. В курсе традиционной логики анализ структуры частных суждений дан обобщенно. Детально особенности частных суждений рассмотрены шотландским логиком У. Гамильтоном (1788—1856) в первой половине XIX века в его «Лекциях по метафизике и логике», им же предложены уточняющие формулировки кванторов как для субъекта суждения, так и для предиката (квантификация предиката).
Общее суждение — суждение о всей без исключения предметной области, на которую направлено внимание, которая является предметом мысли. Это суждение с квантором "все" (ни один, каждый, всякий, без исключения и пр.) перед субъектом: «Все S есть Р», «Ни одно насекомое не есть млекопитающее», «Каждый школьник имеет дневник».
Интерпретация языковых выражений, уточнение объема суждений зачастую представляют собой известную трудность. Так, для человека не знакомого с предметной областью, даже такое простое суждение как "Студенты нашей группы хорошие спортсмены" будет неопределенным в количественном отношении: все или только некоторые студенты группы являются спортсменами. Логика не может сама разрешать такие проблемные ситуации, поэтому столь важно знания специалистов в конкретных предметных областях, потому что только они могут адекватно действительности уточнить некоторые объемные и, тем более, содержательные характеристики суждений.
По качественному признаку, т.е. по характеру связки, простые категорические суждения делятся на утвердительные и отрицательные. Утвердительная связка в русском языке нередко пропускается.
По объединенному качественно-количественному признаку все простые категорические суждения делятся на шесть видов: общеутвердительные, общеотрицательные, частноутвердительные, частноотрицательные, единичноутвердительные и единичноотрицательные. Обычно, в логике все свойства общих суждений переносятся на единичные, ведь субъект единичных суждений, как и субъект общих, полностью исчерпывает свою предметную область, поэтому единичные суждения в особый вид не выделяются.
Оставшиеся четыре вида простых категорических суждений имеют в логике специальные, удобные для формульной записи, буквенные обозначения: А — общеутвердительное, Е — общеотрицательное, I — частноутвердительное, О — частноотрнцательное.
Формальнологический анализ этих суждений позволяет выявить некоторые структурные закономерности их, не зависящие от содержания суждений. Исходя из структуры общих (как утвердительного, так и отрицательного) суждений («Все S есть Р», «Все S не есть Р», или, что одно и то же, «Ни одно S не есть Р»), можно, не зная содержания, сказать, что их субъекты взяты в полном своем объеме (для отрицательного случая - в полном объеме исключаются из рассмотрения). В логике, понятие, взятое в полном своем объеме или в полном объеме исключающееся из рассмотрения, называется распределенным. Таким образом, общее закономерного характера положение для этих суждений формулируется так: субъекты общих суждений всегда распределены. Ясно, что субъекты частных суждений будут всегда нераспределены, ибо речь в них идет лишь о «некоторых S».
Что касается предикатов отрицательных суждений, то, раз они в полном объеме исключаются из рассмотрения - «не есть Р», «не суть Р», значит они всегда распределены. Предикаты же утвердительных суждений свою объемную характеристику проявляют нечетко. Учитывая своеобразие утвердительной связки, могущей выражать как тождество (когда S равно Р), так и подчинение, частичное совпадение (когда S есть только часть Р и когда Р есть только часть S), — приходится заключить: предикаты утвердительных суждений, как правило, нераспределены (взяты только в части своего объема). В тех же особых случаях, когда предикат подчиняется субъекту, т.е. объем его полностью входит в объем субъекта, или когда они тождественны по объему, тогда предикат утвердительных суждений может быть распределенным. Например. «Все квадраты — это ромбы с прямыми углами» или «Некоторые учащиеся — студенты».
Общую картину распределенностн субъекта и предиката в простых категорических суждениях можно представить в следующей таблице, где символ «+» обозначает распределеенность, а символ «—» — нераспределенность (исключительные случаи заключены в скобки):
|
|
|
|
|
|
S |
Р |
|
А |
+ |
--(+) |
|
Е |
+ |
+ |
|
I |
-- |
--(+) |
|
0 |
— |
+ |
§ 3. ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ КАТЕГОРИЧЕСКИМИ СУЖДЕНИЯМИ
Между известными видами простых категорических суждений устанавливаются следующие отношения: противоречия (контрадикторности), противоположности (контрарности, противности), подпротивоположности (субконтрарности, подпротивности, или частичного совпадения) и подчинения.
Отношение противоречия (контрадикторности) устанавливается между суждениями, разными как по качеству, так и по количеству, т.е. между общеутвердительным (А) и частноотрицательным (О) и между общеотрицательным (Е) и частноутвердительным (I).
Отношение противоположности (контрарности, противности) устанавливается между общими суждениями, но разными по качеству: между общеутвердителным (А) и общеотрицательным (Е).
Отношение подпротивоположности (подпротивности, субконтрарности, или частичного совпадения) устанавливается между разными по качеству частными суждениями, (между I и О).
Наконец, в отношении подчинения находятся суждения одинакового качества, но разного количества, т.е. суждения общеутвердительное (А) и частноутвердительное (I), а также общеотрицательное (Е) и частноотрицательное (О). В этом отношении общее есть подчиняющее суждение, частное - подчиненное.
Для наглядности и лучшего запоминания отношений между простыми категорическими суждениями в качестве мнемонической фигуры используют предложенный еще в средневековье так называемый логический квадрат. Углы этого квадрата соответствуют видам суждений, а стороны и диагонали - отношениям между ними:
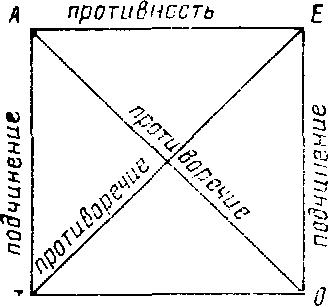
подпротивность
Рассмотрим теперь самое главное - истинностные зависимости суждений, находящихся в этих отношениях. Отношение противоречия (контрадикторности) - самое четкое и определенное, можно сказать, жесткое отношение между суждениями. Противоречащие суждения не могут быть одновременно ни истинными, ни ложными. Это отношение соответствует принципу логики, выраженному законом исключенного третьего, согласно которому, если суждение А (общеутвердительное) истинно, то противоречащее ему суждение О (частноотрицательное) будет обязательно ложным, и наоборот. Таково же отношение и между частноутвердительным (I) суждением и общеотрицательным (Е).
Отношение противоположности (противности, контрарности) неоднозначно. При истинности суждения А (или Е} ему противное суждение Е (или А) будет обязательно ложным. Но при исходной ложности суждения А (или Е), ему противное суждение Е (или А) может быть как истинным, так и ложным, что зависит только от конкретного содержания этих суждений. И снова, в конкретной ситуации лишь специалист в этой предметной области может окончательно решить, каким именно по истинностному своему значению будет противоположное исходному суждение.
Например, исходное общеутвердительное (А) суждение «Все люди есть студенты» — ложно. По логике, противное ему суждение может быть как истинным, так и ложным. Зная предметную область, мы эту неопределенность снимаем и заключаем, что противное исходному общеотрицательное суждение (Е) «Ни один человек не является студентом» тоже ложно. Но вот другое по конкретному содержанию исходное суждение «Все люди имеют крылья». Оно тоже ложно, однако противное ему суждение «Ни один человек не имеет крыльев» — истинно. Особенность противоположных суждений кратко формулируется следующим образом: противоположные суждения не могут быть одновременно истинными, по крайней мере одно из них ложно, по большей мере - оба могут быть ложными.