ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2019
Просмотров: 12627
Скачиваний: 26
101
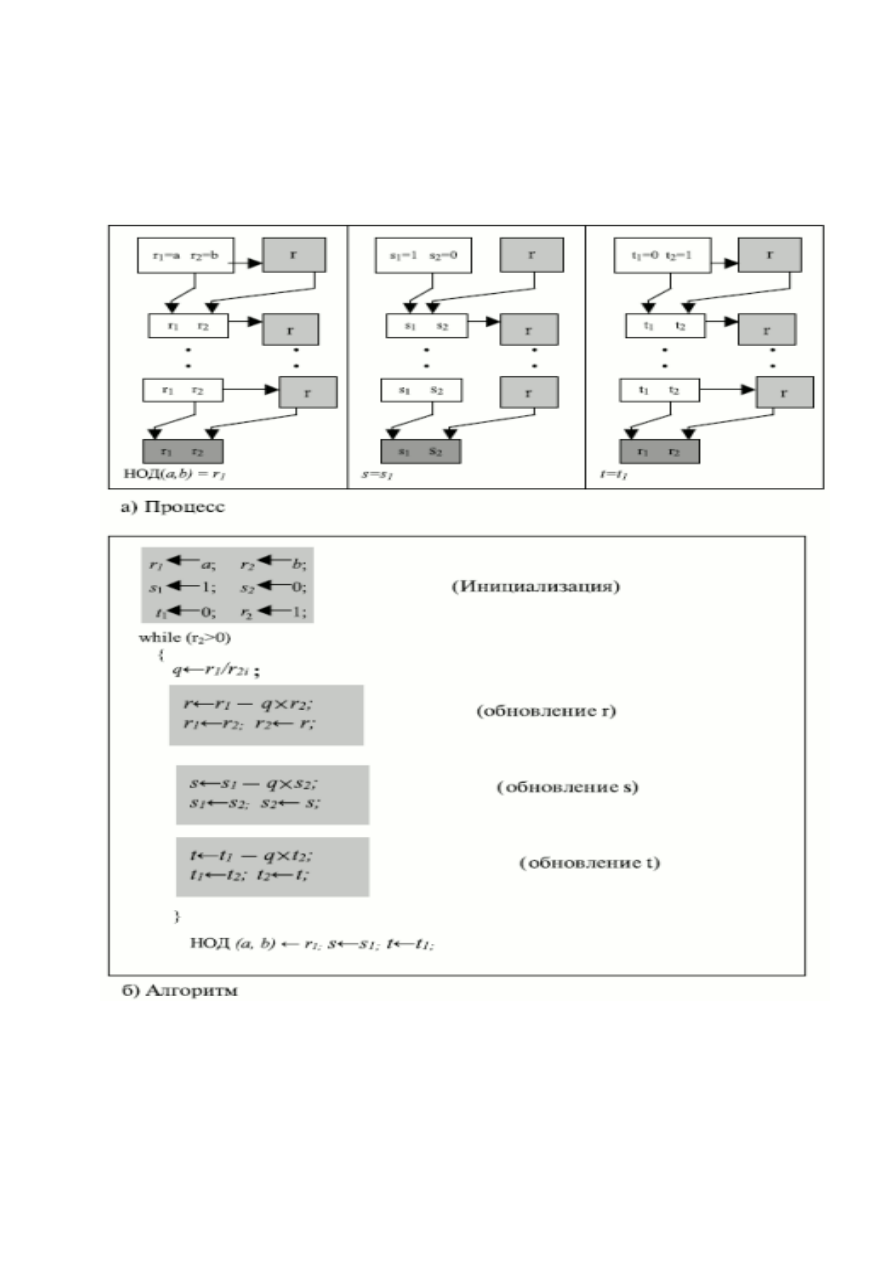
Здесь расширенный алгоритм Евклида использует те же самые шаги,
что и простой алгоритм Евклида. Однако в каждом шаге мы применяем три
группы вычислений вместо одной. Алгоритм использует три набора
переменных:
r
,
s
и
t
.
Рис. 2.8.
Расширенный алгоритм Евклида
На каждом шаге переменные
r
1
,
r
2
и
r
используются так же, как в
алгоритме
Евклида.
Переменным
r
1
и
r
2
присваиваются
начальные
значения
a
и
b
соответственно. Переменным
s
1
и
s
2
присваиваются начальные
102
значения
1
и
0
соответственно. Переменным
t
1
и
t
2
присваиваются начальные
значения
0
и
1
, соответственно. Вычисления
r
,
s
и
t
одинаковы, но с одним
отличием. Хотя
r
— остаток от деления
r
1
на
r
2
, такого соответствия в других
двух группах вычислений нет. Есть только одно частное,
q
, которое
вычисляется как
r
1
/r
2
и используется для других двух вычислений.
Пример 2.9
Дано
a = 161
и
b = 28
, надо найти
НОД (a, b)
и значения
s
и
t
.
Решение
r = r
1
– q x r
2
s = s
1
– qs
2
t = t
1
– q x t
2
Для отображения алгоритма мы используем следующую таблицу:
q r
1
r
2
R s
1
s
2
s t
1
t
2
t
5 161 28 21 1 0 1 0 1
-5
1 28
21 7
0 1 -1 1 -5
6
3 21
7
0
1 -1 4 -5 6
-23
7
0
-1 4
6 -23
Мы получаем
НОД (161, 28) = 7
,
s = –1
и
t = 6
. Ответы могут быть
проверены, как это показано ниже.
(–1) x 161 + 6 x 28 = 7
Пример 2.10
Дано
a = 17
и
b = 0
, найти
НОД (a, b)
и значения
s
и
t
.
Решение
Для отображения алгоритма мы используем таблицу.
q r
1
r
2
R s
1
s
2
s t
1
t
2
t
17 0 1 0 0 1
Обратите внимание, что нам не надо вычислять
q
,
r
и
s
. Первое
значение
r
2
соответствует
условию
завершения
алгоритма.
Мы
получаем
НОД (17, 0) = 17
,
s = 1
и
t = 0
. Это показывает, почему мы должны
придавать начальные значения
s
1
— 1
и
t
1
—
0
. Ответы могут быть проверены
так, как это показано ниже:
(1 x 17) + (0 x 0) = 17
Пример 2.11
Даны
a = 0
и
b = 45
, найти
НОД (a, b)
и значения
s
и
t
.
Решение
Для отображения алгоритма мы используем следующую таблицу:
103
q r
1
r
2
R s
1
s
2
s t
1
t
2
t
0 0 45 0 1 0 1 0 1 0
45 0 0 1 0 1
Мы получаем
НОД (0,45) = 45
,
s = 0
и
t = 1
. Отсюда ясно, что мы
должны инициализировать
s
2
равным
0
, а
t
2
— равным
1
. Ответ может быть
проверен, как это показано ниже:
(0 x 0) + (1 x 45) = 45
4.2. Модульная арифметика
Уравнение деления (
), рассмотренное в предыдущей секции,
имеет два входа (
a
и
n
) и два выхода (
q
и
r
). В модульной арифметике мы
интересуемся только одним из выходов — остатком
r
. Мы не заботимся о
частном
q
. Другими словами, когда мы делим
a
на
n
, мы интересуемся только
тем, что
значение остатка равно
r
. Это подразумевает, что мы можем
представить изображение вышеупомянутого уравнения как бинарный
оператор с двумя входами
a
и
n
и одним выходом
r
.
Операции по модулю
Вышеупомянутый бинарный оператор назван
оператором по модулю
и
обозначается как
mod
. Второй вход (
n
) назван
модулем
.
Выход (остаток)
r
назван
вычетом
деления по сравнению с оператором по модулю.
Рис. 2.9.
Соотношение уравнения деления и оператора по модулю
, оператор по модулю (
mod
) выбирает целое число
(
a
) из множества
Z
и положительный модуль (
n
). Оператор определяет
неотрицательный остаток (
r
).
Мы можем сказать, что
a mod n = r
Пример 2.14
Найти результат следующих операций:
a.
27 mod 5
b.
36 mod 12
104
c.
–18 mod 14
d.
–7 mod 10
Решение
Мы ищем вычет
r
. Мы можем разделить
a
на
n
и найти
q
и
r
. Далее можно
игнорировать
q
и сохранить
r
.
а. Разделим
27
на
5
- результат:
r = 2
. Это означает, что
27 mod 5 = 2
.
б. Разделим
36
на
12
— результат:
r = 0
. Это означает, что
36 mod 12 = 0
.
в. Разделим
(–18)
на
14
— результат:
r = –4
. Однако мы должны прибавить
модуль
(14)
, чтобы сделать остаток неотрицательным. Мы имеем
r = –4 + 14
= 10
. Это означает, что
–18 mod 14 = 10
.
г. Разделим
(–7)
на
10
— результат:
r = –7
. После добавления модуля
–7
мы
имеем
r = 3
. Это означает, что
–7 mod 10 = 3
.
Система вычетов: Zn
Результат операции по модулю
n
— всегда целое число между
0
и
n - 1
.
Другими словами, результат
a mod n
— всегда неотрицательное целое число,
меньшее, чем
n
. Мы можем сказать, что операция по модулю создает набор,
который в модульной арифметике можно понимать как
систему
наименьших вычетов по модулю n
, или
Z
n
. Однако мы должны помнить,
что хотя существует только одно множество целых чисел (
Z
), мы имеем
бесконечное число множеств вычетов (
Z
n
), но лишь одно для каждого
значения
n
множество
Z
n
и
три
множества
Z
2
,
Z
6
и
Z
11
.
Рис. 2.10.
Некоторые наборы Zn
Сравнения
В криптографии мы часто используем понятие
сравнения
вместо
равенства. Отображение
Z
в
Z
n
не отображаются "один в один". Бесконечные
элементы множества
Z
могут быть отображены одним элементом
Z
n
.
Например, результат
2 mod 10 = 2
,
12 mod 10 = 2
,
22 mod 10 = 2
, и так далее.
В модульной арифметике целые числа, подобные
2
,
12
, и
22
, называются
сравнимыми по модулю
10 (mod 10)
. Для того чтобы указать, что два целых
числа
сравнимы, мы
используем
оператор
сравнения
(
).
Мы
добавляем
mod n
к правой стороне сравнения, чтобы определить значение
модуля и сделать равенство правильным. Например, мы пишем:
105
показывает принцип сравнения. Мы должны объяснить
несколько положений.
a. Оператор сравнения напоминает оператор равенства, но между ними
есть различия. Первое: оператор
равенства
отображает элемент
Z
самого на
себя; оператор
сравнения
отображает элемент
Z
на элемент
Z
n
. Второе:
оператор равенства показывает, что наборы слева и справа соответствуют
друг другу "один в один", оператор сравнения — "многие — одному".
Рис. 2.11.
Принцип сравнения
б. Обозначение (
mod n
), которое мы вставляем с правой стороны
оператора сравнения, обозначает признак множества (
Z
n
). Мы должны
добавить это обозначение, чтобы показать, какой модуль используется в
отображении. Символ, используемый здесь, не имеет того же самого
значения, как бинарный оператор в уравнении деления. Другими словами,
символ
mod
в выражении
12 mod 10
— оператор; а сочетание (
mod 10
) в
сравнении
означает, что набор —
Z
10
.
Система вычетов
Система вычетов
[a]
, или
[a]
n
, — множество целых чисел, сравнимых
по модулю
n
. Другими словами, это набор всех целых чисел, таких, что
x = a
(mod n)
. Например, если
n = 5
, мы имеем множество из пяти
элементов
[0]
,
[1]
,
[2]
,
[3]
и
[4]
, таких как это показано ниже:
[0] = {…., –15, -10, –5, 0, 5, 10, 15, …}
[1] = {…., –14, –9, –4, 1, 6 , 11, 16,…}
[2] = {…., –13, –8, –3, 2, 7, 12, 17,…}
[3] = {...., –12, –7, –2, 3, 8, 13, 18,…}
[4] = {…., –11, –6, –1, 4, 9, 14, 19,…}