Добавлен: 29.10.2018
Просмотров: 48188
Скачиваний: 190

496
Глава 6. Взаимоблокировка
показана на рис. 6.2, л, а не ту, которая показана на рис. 6.2, г. Эта последовательность
отображается ресурсным графом, показанным на рис. 6.2, м–с, и не приводит к взаи-
моблокировке.
По окончании этапа, показанного на рис. 6.2, с, процессу B может быть выделен ресурс
S, поскольку процесс A завершил свою работу, а процесс C имеет все необходимое.
Даже если B заблокируется при запросе ресурса T, взаимоблокировки не возникнет.
Процесс B просто будет ждать, пока процесс C не завершит свою работу.
Далее в этой главе будет подробно рассмотрен алгоритм принятия решений по распре-
делению ресурсов, которые не приводят к взаимоблокировкам. А сейчас нужно понять,
что ресурсные графы являются инструментом, позволяющим понять, приводит ли
данная последовательность запросов/возвратов ресурсов к взаимоблокировке. Мы
всего лишь шаг за шагом осуществляем запросы и возвраты ресурсов и после каждого
шага проверяем граф на наличие каких-либо циклов. Если образуется цикл, значит,
возникла взаимоблокировка, а если нет, значит, нет и взаимоблокировки. Хотя здесь
рассматривался граф ресурсов, составленный для случая использования по одному
ресурсу каждого типа, ресурсные графы могут быть применены также для обработки
нескольких ресурсов одного и того же типа (Holt, 1972).
Чаще всего для борьбы с взаимными блокировками используются четыре стратегии:
1. Игнорирование проблемы. Может быть, если вы проигнорируете ее, она проиг-
норирует вас.
2. Обнаружение и восстановление. Дайте взаимоблокировкам проявить себя, обна-
ружьте их и выполните необходимые действия.
3. Динамическое уклонение от них за счет тщательного распределения ресурсов.
4. Предотвращение за счет структурного подавления одного из четырех условий,
необходимых для их возникновения.
В следующих четырех разделах будут рассмотрены по порядку каждый из этих методов.
6.3. Страусиный алгоритм
Самым простым подходом к решению проблемы является «страусиный алгоритм»:
спрячьте голову в песок и сделайте вид, что проблема отсутствует
1
. Люди реагируют
на эту стратегию по-разному. Математики считают ее неприемлемой и говорят, что
взаимоблокировки следует предотвращать любой ценой. Инженеры спрашивают, как
часто ожидается возникновение проблемы, как часто система дает сбой по другим при-
чинам и насколько серьезны последствия взаимоблокировки. Если взаимоблокировка
возникает в среднем один раз в пять лет, а система раз в неделю сбоит из-за технических
отказов и дефектов операционной системы, большинство инженеров не захотят платить
за избавление от взаимоблокировок существенным снижением производительности
или удобства использования.
1
Вообще-то эта байка не соответствует действительности. Страус может развивать скорость
60 км/ч, а силы его удара ногой достаточно, чтобы убить любого льва, решившего устроить
себе шикарный обед из страуса, и львы об этом знают. — Примеч. ред.

6.4. Обнаружение взаимоблокировок и восстановление работоспособности
497
Чтобы усилить контраст между этими двумя позициями, рассмотрим операционную
систему, которая блокирует вызывающий процесс, когда системный вызов open, отно-
сящийся к такому физическому устройству, как привод Blu-ray-диска или принтер, не
может быть выполнен из-за занятости устройства. Обычно именно драйвер устройства
решает, какое действие и при каких обстоятельствах предпринять. Две вполне оче-
видные возможности — это блокировка или возвращение кода ошибки. Если одному
процессу удастся «открыть» привод Blu-ray-дисков, а другому посчастливится «от-
крыть» принтер, а затем каждый процесс попытается «открыть» еще и другой ресурс
и его попытка будет заблокирована, возникнет взаимоблокировка. Лишь немногие
современные системы в состоянии обнаружить подобную ситуацию.
6.4. Обнаружение взаимоблокировок
и восстановление работоспособности
Вторая по счету — технология обнаружения и восстановления. При ее использовании
система не пытается предотвращать взаимоблокировки. Она позволяет им произойти,
пытается обнаружить момент их возникновения, а затем предпринимает некоторые
действия по восстановлению работоспособности. В этом разделе будут рассмотрены
некоторые способы обнаружения взаимоблокировок и некоторые методы восстанов-
ления работоспособности, которые можно реализовать.
6.4.1. Обнаружение взаимоблокировки при использовании
одного ресурса каждого типа
Начнем с самого простого случая, когда используется только один ресурс каждого
типа. У системы может быть один сканер, один пишущий привод Blu-ray-дисков, один
плоттер и один накопитель на магнитной ленте, но только по одному экземпляру каж-
дого класса ресурсов. Иными словами, мы временно исключаем системы, имеющие два
принтера. Они будут рассмотрены позже с использованием другого метода.
Для такой системы можно построить ресурсный граф (рис. 6.1). Если этот граф содер-
жит один и более циклов, значит, мы имеем дело с взаимоблокировкой. Любой процесс,
являющийся частью цикла, заблокирован намертво. Если циклов нет, значит, система
не находится в состоянии взаимоблокировки.
В качестве примера более сложной системы по сравнению с ранее рассмотренными,
возьмем систему с семью процессами от A до G и шестью ресурсами от R до W. Каж-
дый ресурс находится в состоянии текущей занятости, и на каждый ресурс в данный
момент поступил запрос:
1. Процесс A удерживает R и хочет получить S.
2. Процесс B не удерживает никаких ресурсов, но хочет получить T.
3. Процесс C не удерживает никаких ресурсов, но хочет получить S.
4. Процесс D удерживает U и хочет получить S и T.
5. Процесс E удерживает T и хочет получить V.
6. Процесс F удерживает W и хочет получить S.
7. Процесс G удерживает V и хочет получить U.
498
Глава 6. Взаимоблокировка
Возникает следующий вопрос: «Находится ли эта система в состоянии взаимоблоки-
ровки, и если находится, то какие процессы вовлечены в это состояние?»
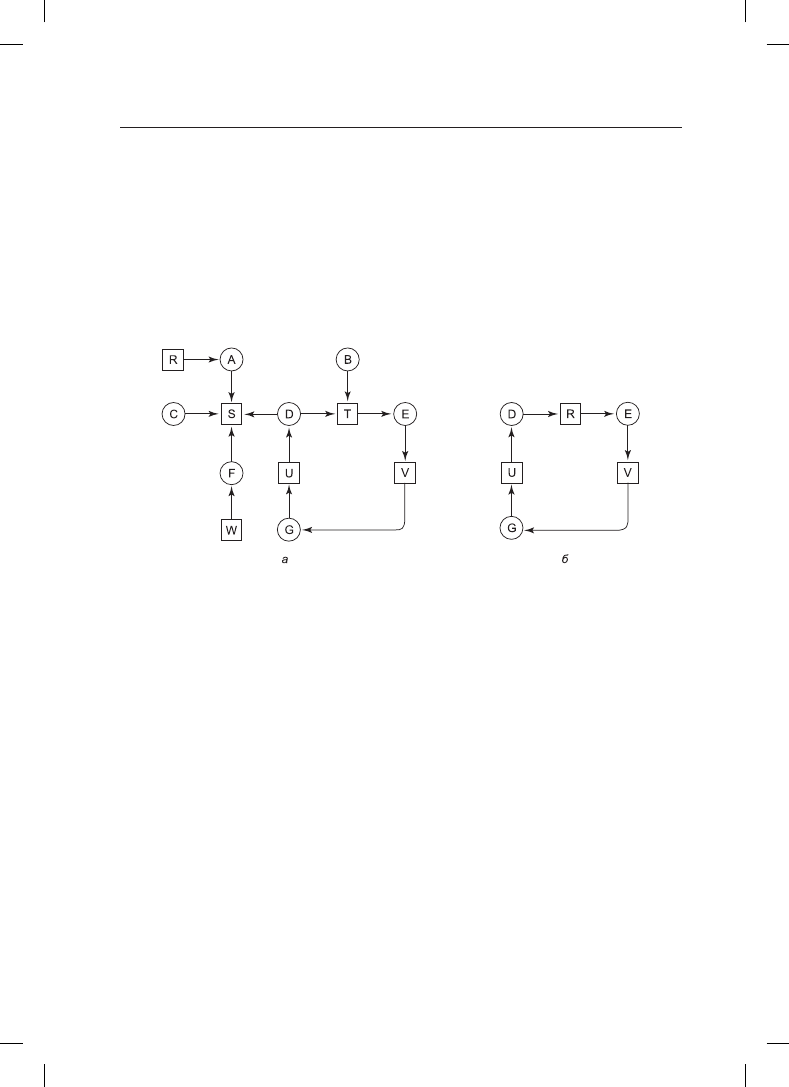
Чтобы ответить на этот вопрос, можно построить граф ресурсов (рис. 6.3, а). Этот
граф содержит один цикл, который можно обнаружить визуально. Этот цикл показан
на рис. 6.3, б. Из цикла видно, что процессы D, E и G вовлечены во взаимоблокировку.
Процессы A, C и F не находятся в состоянии взаимоблокировки, поскольку ресурс S
может быть выделен любому из них, который затем закончит свою работу и вернет
ресурс. Затем оставшиеся два процесса смогут взять его по очереди и также завершить
свою работу. (Заметьте, чтобы сделать этот пример немного интереснее, мы позволили
процессам, а именно процессу D, запрашивать одновременно два ресурса.)
Рис. 6.3. а — граф ресурсов; б — извлеченный из него цикл
Хотя визуально выделить взаимоблокировку из простого графа относительно нетруд-
но, для использования в настоящих системах нужен формальный алгоритм обнару-
жения взаимоблокировок. Известно множество алгоритмов для обнаружения циклов
в направленных графах. Далее будет приведен простой алгоритм, проверяющий граф
и прекращающий свою работу либо при обнаружении цикла, либо при обнаружении
отсутствия циклов. В нем используется одна динамическая структура данных, L, пред-
ставляющая собой список узлов, а также список ребер. В процессе работы алгоритма
ребра будут помечаться для обозначения того, что они уже были проверены, чтобы
предотвратить повторные проверки.
Действие алгоритма основано на выполнении следующих шагов:
1. Для каждого узла N, имеющегося в графе, выполняются следующие пять шагов,
использующих узел N в качестве начального.
2. Инициализируется (очищается) список L, а со всех ребер снимаются пометки.
3. Текущий узел добавляется к концу списка L, и проводится проверка, не появит-
ся ли этот узел в списке L дважды. Если это произойдет, значит, граф содержит
цикл (отображенный в списке L), и алгоритм прекращает работу.
4. Для заданного узла определяется, нет ли каких-нибудь отходящих от него непо-
меченных ребер. Если такие ребра есть, осуществляется переход к шагу 5, если их
нет, осуществляется переход к шагу 6.

6.4. Обнаружение взаимоблокировок и восстановление работоспособности
499
5. Произвольно выбирается и помечается непомеченное отходящее от узла ребро.
Затем по нему осуществляется переход к новому текущему узлу, и алгоритм воз-
вращается к шагу 3.
6. Если этот узел является первоначальным узлом, значит, граф не содержит никаких
циклов, и алгоритм завершает свою работу. В противном случае алгоритм зашел
в тупик. Этот узел удаляется, и алгоритм возвращается к предыдущему узлу, то
есть к тому узлу, который был текущим перед только что удаленным узлом. Дан-
ный узел делается текущим, и осуществляется переход к шагу 3.
Этот алгоритм берет поочередно каждый узел в качестве корневого в надежде, что
из этого получится дерево, и выполняет в дереве поиск в глубину. Если в процессе
обхода алгоритм возвращается к уже встречавшемуся узлу, значит, он нашел цикл.
Если алгоритм обходит все ребра из какого-нибудь заданного узла, то он возвращается
к предыдущему узлу. Если он возвращается к корневому узлу и не может идти дальше,
то подграф, доступный из текущего узла, не содержит циклов. Если данное свойство
сохраняется для всех узлов, значит, полный граф не содержит циклов, а система не
находится в состоянии взаимоблокировки.
Чтобы увидеть на практике работу этого алгоритма, воспользуемся графом, изо-
браженным на рис. 6.3, а. Порядок обработки узлов произвольный, поэтому будем
исследовать их слева направо и сверху вниз, выбрав при первом запуске алгоритма
начальный узел R, затем последовательно выбирая узлы A, B, C, S, D, T, E, F и т. д. Если
мы обнаружим цикл, алгоритм прекратит свою работу.
Начинаем с узла R и инициализируем L как пустой список. Затем добавляем узел R
в список, переходим к единственно возможному узлу A и также добавляем его к спи-
ску L, получая L = [R, A]. Из узла A следуем к узлу S, получая L = [R, A, S]. Узел S не
имеет отходящих от него ребер, следовательно, это тупик, который заставляет нас
вернуться к узлу A. Так как у узла A также нет немаркированных отходящих от него
ребер, мы возвращаемся к узлу R, завершая таким образом его исследование.
Теперь перезапускаем алгоритм, начиная его работу с узла A и предварительно вернув
список L в исходное состояние. Этот поиск также быстро остановится, поэтому начнем
снова с узла B. Из узла B проследуем по отходящим ребрам до тех пор, пока не доберем-
ся до узла D; к этому моменту список будет иметь следующий вид: L = [B, T, E, V, G, U,
D]. Теперь нужно сделать произвольный выбор. Если выбрать узел S, мы попадаем в ту-
пик и возвращаемся к узлу D. Во второй раз выбираем узел T и обновляем список L до
вида [B, T, E, V, G, U, D, T], где обнаруживаем цикл и останавливаем работу алгоритма.
Этот алгоритм еще далек от оптимального. Более удачный алгоритм показан в работе
Эвена (Even, 1979). Тем не менее приведенный пример доказывает само существование
алгоритма для обнаружения взаимоблокировки.
6.4.2. Обнаружение взаимоблокировки при использовании
нескольких ресурсов каждого типа
Когда в системе существует несколько экземпляров каких-нибудь ресурсов, для об-
наружения взаимоблокировки необходим другой подход. Сейчас будет представлен
алгоритм, основанный на использовании матриц и предназначенный для обнаружения
взаимоблокировки при работе n процессов, от P
1
до P
n
. Пусть m — это число классов ре-
сурсов, Е
1
— количество ресурсов класса 1, Е
2
— количество ресурсов класса 2, а в общем

500
Глава 6. Взаимоблокировка
E
i
— количество ресурсов класса i (где 1 ≤ i ≤ m). E — это вектор существующих ресурсов.
Он передает общее количество имеющихся в наличии экземпляров каждого ресурса.
Например, если класс 1 представляет собой накопители на магнитных лентах, то E
1
= 2
означает, что в системе есть два таких накопителя.
В любой момент времени какие-то ресурсы могут быть выделены и недоступны. Пусть
A будет вектором доступных ресурсов, где A
i
дает количество экземпляров ресурса i,
доступных на данный момент (то есть не выделенных). Если оба накопителя на маг-
нитной ленте уже выделены, A
1
будет равно 0.
Теперь нам нужны два массива: C — матрица текущего распределения и R — матрица
запросов
. i-я строка в матрице C говорит о том, сколько экземпляров каждого класса
ресурсов в данный момент удерживает процесс P
i
. Таким образом, C
ij
— это количество
экземпляров ресурса j, которое удерживается процессом i. По аналогии с этим R
ij
—
это количество экземпляров ресурса j, которое хочет получить процесс P
i
. Все четыре
структуры данных показаны на рис. 6.4.
Рис. 6.4. Четыре структуры данных, необходимые для работы алгоритма
обнаружения взаимоблокировок
Для этих четырех структур данных сохраняется одно важное соотношение. А имен-
но — каждый ресурс является либо выделенным, либо доступным. Это наблюдение
означает, что
Иными словами, если сложить все уже выделенные экземпляры ресурса j и к ним
прибавить все еще доступные экземпляры, в результате получится количество суще-
ствующих экземпляров ресурса этого класса.
Алгоритм обнаружения взаимоблокировок основан на сравнении векторов. Определим,
что для двух векторов A и B сооотношение A ≤ B означает, что каждый элемент вектора
A меньше или равен соответствующему элементу вектора B. Математически это можно
записать так: A ≤ B тогда и только тогда, когда A
i
≤ B
i
для 1 ≤ i ≤ m.
Каждый процесс изначально объявляется немаркированным. По мере работы процессы
будут помечаться, показывая, что они способны завершить свою работу и не участвуют
во взаимоблокировке. Когда алгоритм завершает свою работу, любой непомеченный