Добавлен: 29.10.2018
Просмотров: 48143
Скачиваний: 190

686
Глава 9. Безопасность
бражение и стеганографический инструментарий, необходимый для извлечения пьес.
В это трудно поверить, но попробуйте, и перед вами раскроется невероятное зрелище.
Еще одним применением стеганографии может стать добавление в изображения, ис-
пользуемые на веб-страницах, скрытых водяных знаков, чтобы обнаружить их кражу
и использование на других веб-страницах. Если ваша веб-страница содержит изо-
бражение с секретным сообщением «Copyright 2014, General Images Corporation», то
трудно будет доказать судье, что вы сами изготовили это изображение. Данный метод
может использоваться также для защиты водяными знаками музыки, фильмов и т. д.
Разумеется, существование подобных водяных знаков наталкивает некоторых специ-
алистов на поиск способов их удаления. Схема, при которой информация хранится
в битах младших разрядов, может быть нарушена путем вращения изображения на 1°
по часовой стрелке, затем конвертирования его в систему с потерей качества, напри-
мер JPEG, а затем вращения его обратно на 1°. И наконец, изображение может быть
обратно конвертировано в исходную систему кодировки (например, GIF, BMP, TIF).
JPEG-конвертирование с потерей качества перемещает биты младших разрядов, а вра-
щение потребует объемных вычислений с плавающей запятой, при которых возникают
ошибки округления, также добавляющие шум в биты младших разрядов. Специалисты,
вставляющие водяные знаки, знают об этом (или должны знать об этом), поэтому они
помещают свою информацию об авторских правах с избытком и применяют схемы,
в которых используются не только биты младших разрядов из пикселов. Такое по-
ложение вещей подстегивает атакующих выискивать более изощренные технологии
удаления. И эта борьба не прекращается.
Стеганография может использоваться для организации скрытой утечки информации, но
чаще всего возникает желание сделать наоборот: скрыть информацию от любопытных
глаз взломщика, при этом не обязательно скрывая тот факт, что мы ее прячем. Подобно
Юлию Цезарю мы хотим убедиться, что даже если наши сообщения или файлы попадут
в чужие руки, злоумышленник не сможет обнаружить в них секретную информацию.
Эта область относится к криптографии, которая и станет темой следующего раздела.
9.5. Основы криптографии
Криптография играет весьма существенную роль в обеспечении безопасности. Многие
люди знакомы с газетными криптограммами — небольшими головоломками, в которых
каждая буква по определенной системе заменяется другой буквой. К современной
криптографии они имеют такое же отношение, как хот-доги к изысканной кулинарии.
В этом разделе будет дан весьма краткий обзор криптографии компьютерной эпохи.
Как уже упоминалось, криптография используется в операционных системах во мно-
гих местах. Например, некоторые файловые системы могут зашифровать все данные
на диске, такие протоколы, как IPSec, позволяют зашифровать и/или подписать все
сетевые пакеты, а большинство операционных систем шифруют пароли, чтобы не дать
взломщикам возможности их восстановления. Более того, в разделе 9.6 будет рассмо-
трена роль шифрования в другом важном аспекте безопасности — аутентификации.
Нами будут рассмотрены основные элементы, используемые этими системами. Но
серьезное рассмотрение вопросов криптографии не входит в задачи данной книги.
Подробному рассмотрению данной темы посвящено множество замечательных книг по
компьютерной безопасности. Заинтересовавшимся можно предложить, к примеру, кни-
ги Kaufman et al. (2002), Gollman (2011). Далее будет дано весьма краткое рассмотрение
вопросов криптографии для тех читателей, которые с ними никогда не сталкивались.
9.5. Основы криптографии
687
Замысел криптографии заключается в том, чтобы закодировать открытый текст (plain-
text) — сообщение или файл, превратив его в зашифрованный текст (ciphertext), чтобы
о том, как его снова превратить в открытый текст, знали только те, кто имеет на это право.
Для всех остальных зашифрованный текст будет лишь непонятным набором битов. Как
бы странно это ни прозвучало для новичков, но алгоритмы (функции), используемые
для шифрования и дешифрования, всегда должны быть открытыми. Попытка хранить их
в секрете практически никогда не срабатывает и создает у людей, пытающихся сохранить
секреты, ложное чувство безопасности. В коммерции такая тактика называется безопас-
ностью за счет неизвестности
(security by obscurity) и используется только дилетантами.
Как ни странно, но в эту категорию попадает множество транснациональных корпораций,
сотрудникам которых следовало бы получше изучить данный вопрос.
При реальном подходе к делу безопасность зависит от параметров алгоритмов, на-
зываемых ключами. Если P — это файл с обычным текстом, KE — ключ шифрования,
C — зашифрованный текст и E — алгоритм шифрования (то есть функция), то C = E(P,
KE). Это и есть определение шифрования. Из него следует, что зашифрованный текст
получается за счет использования известного алгоритма шифрования E с параметрами,
в качестве которых выступает открытый текст P и секретный ключ шифрования, KE.
Идея, предполагающая использование открытого алгоритма и содержание секретности
исключительно в ключах, называется принципом Керкгоффса (Kerckhoffs’ Principle).
Он был сформулирован голландским криптографом XIX века Огюстом Керкгоффсом.
Сегодня этой идеи придерживаются все серьезные криптографы.
Аналогично прежней формуле, P = D(C, KD), где D — это алгоритм дешифрования,
а KD — ключ дешифрования. Согласно этой формуле, чтобы получить обычный текст P
из зашифрованного текста C при наличии ключа дешифрования KD, нужно запустить
алгоритм D, используя C и KD в качестве параметров. Взаимоотношения между раз-
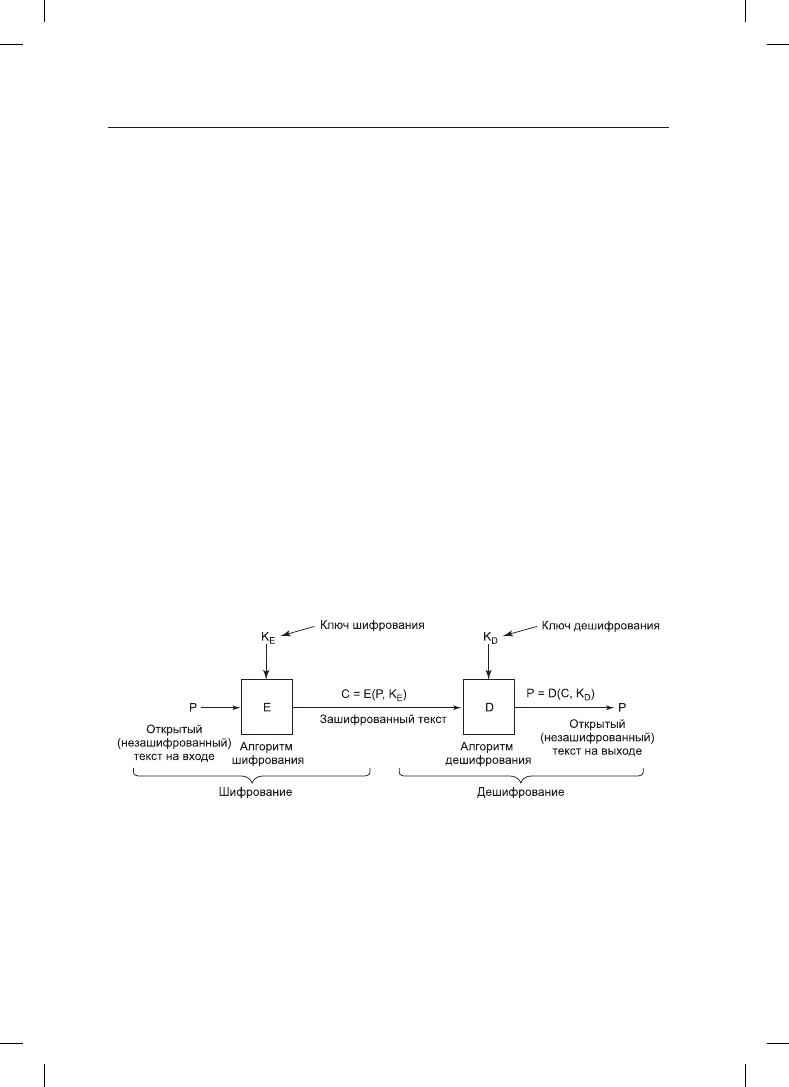
личными компонентами показаны на рис. 9.13.
Рис. 9.13. Взаимоотношения между открытым и зашифрованным текстом
9.5.1.Шифрование с секретным ключом
Чтобы прояснить вышеизложенное, рассмотрим алгоритм шифрования, в котором
каждая буква заменяется другой буквой, например все буквы A заменяются буквами Q,
все буквы B — буквами W, все буквы C — буквами E и т. д., как показано в этом примере:
открытый текст: ABCDEFGHIJKLMNOPQRSTUVWXYZ
зашифрованный текст: QWERTYUIOPASDFGHJKLZXCVBNM

688
Глава 9. Безопасность
Такая общая схема называется моноалфавитной подстановкой (monoalphabetic
substitution), где ключом служит строка из 26 букв, соответствующая полно-
му алфавитному набору. В данном примере ключ шифрования QWERTYUIOPAS-
DFGHJKLZXCVBNM. С этим ключом открытый текст ATTACK будет превращен
в зашифрованный текст QZZQEA. Ключ дешифрования сообщает о том, как из за-
шифрованного получить открытый текст. В данном примере ключ дешифрования
KXVMCNOPHQRSZYIJADLEGWBUFT, поскольку A в зашифрованном тексте соответ-
ствует K в открытом тексте, B — X и т. д.
На первый взгляд может показаться, что это вполне безопасная система, поскольку,
несмотря на то что криптографам известна общая схема (побуквенная подстановка),
они не знают, какой из 26! ≈ 4 · 10
26
возможных ключей используется. Тем не менее,
получив на удивление небольшое количество зашифрованного текста, они запросто
могут взломать шифр. Обычно вскрытие удается за счет учета статических свойств
национальных языков. Например, в английском языке наиболее часто встречается
буква e, за которой следуют буквы t, o, a, n, i и т. д. Наиболее частыми двухбуквенными
комбинациями, называемыми биграммами, являются th, in, er, re и т. д. При использо-
вании этой информации взлом шифра не представляет особого труда.
Многие криптографические системы наподобие этой имеют свойство, позволяющее
при наличии ключа шифрования легко определять ключ дешифрования. Подобные
системы называются шифрованием с секретным ключом (secret-key cryptography),
или шифрованием с симметричным ключом (symmetric-key cryptography). При всей
абсолютной непригодности шифрования с моноалфавитной подстановкой известны
другие алгоритмы с симметричным ключом, которые при достаточной длине ключа
обладают относительной высокой стойкостью. Для обеспечения реальной безопасности
должен использоваться ключ длиной минимум 256 бит, обеспечивающий пространство
перебора ключей, равное 2
256
≈ 1,2 · 10
77
. Менее длинные ключи могут противостоять
любителям, но не усилиям специалистов правительственных структур.
9.5.2. Шифрование с открытым ключом
Эффективность систем с секретным ключом обусловлена вполне приемлемым объемом
вычислений, необходимых для шифрования или дешифрования сообщения, но у них
имеется серьезный недостаток: и отправитель и получатель должны владеть общим
секретным ключом. Для передачи ключа им, возможно, даже потребуется физический
контакт. Чтобы обойти эту проблему, применяется шифрование с открытым ключом
(public-key cryptography) (Diffie and Hellman, 1976). Эти системы обладают свойством,
при котором для шифрования и дешифрования используются различные ключи и при
наличии удачно подобранного ключа шифрования практически невозможно вскрыть
соответствующий ключ дешифрования. При таких обстоятельствах ключ шифрования
можно сделать открытым, а в секрете держать только ключ дешифрования.
Чтобы получить начальное представление о шифровании с открытым ключом, рас-
смотрим следующие два вопроса:
1. Сколько будет 314159265358979 · 314159265358979?
2. Чему равен квадратный корень из числа 3912571506419387090594828508241?
Большинство шестиклассников, если дать им бумагу и карандаш и пообещать за
правильный ответ большой пломбир с сиропом, смогут ответить на первый вопрос за

9.5. Основы криптографии
689
один-два часа. Большинство взрослых людей, получив карандаш, бумагу и обещание
пожизненной 50 %-ной налоговой скидки, вообще не смогут решить вторую задачу без
калькулятора, компьютера или другой посторонней помощи. Хотя возведение в квадрат
и извлечение квадратного корня являются по отношению друг к другу обратными опе-
рациями, они существенно различаются в сложности вычислений. Подобные формы
асимметрии служат основой для шифрования с открытым ключом. При шифровании
используется простая операция, но дешифрование без ключа потребует от вас выпол-
нения весьма трудоемкой операции.
В системе шифрования с открытым ключом RSA используется то обстоятельство, что
перемножить большие числа намного проще, чем разложить их на множители, особенно
когда применяется модульная арифметика, а все используемые большие числа состоят
из сотен цифр (Rivest et al., 1978). В криптографическом мире эта система нашла до-
вольно широкое применение. Также применяются системы, основанные на дискретных
логарифмах (El Gamal, 1985). Основная проблема систем шифрования с открытым
ключом состоит в том, что они работают в тысячи раз медленнее, чем системы симме-
тричного шифрования.
Способ работы шифрования с открытым ключом заключается в том, что все получают
пару (открытый ключ, закрытый ключ), а открытый ключ публикуется. Открытый
ключ является ключом шифрования, а закрытый — ключом дешифрования. Обычно
генерация ключей происходит в автоматическом режиме, возможно, с использованием
выбранного пользователем пароля в качестве передаваемого алгоритму начального чис-
ла. Для отправки пользователю секретного сообщения корреспондент зашифровывает
текст этого сообщения открытым ключом получателя. Поскольку закрытый ключ есть
только у получателя, только он в состоянии расшифровать сообщение.
9.5.3. Односторонние функции
Существует множество различных ситуаций, рассматриваемых далее, в которых требу-
ется наличие некой функции f, обладающей свойством, позволяющим при заданной f
и ее параметре x без труда вычислить y = f(x), но не позволяющим путем вычислений
найти значение x, когда задана лишь f(x). Такая функция, как правило, неким сложным
образом искажает последовательность битов. Вначале она может присвоить y значе-
ние x. Затем в ней может использоваться цикл, выполняющийся столько раз, сколько
единичных битов содержится в x, когда при каждом проходе биты y переставляются
неким способом, зависящим от номера прохода. При этом при каждом проходе добав-
ляются разные константы, и в целом биты перемешиваются практически полностью.
Такие функции называются криптографическими хэш-функциями (cryptographic
hash function).
9.5.4. Цифровые подписи
Потребность в цифровой подписи документа возникает довольно часто. Представим,
например, банковского клиента, дающего банку по электронной почте поручение
купить для него акции. Через час после отправки и выполнения поручения акции
рухнули. Теперь клиент отрицает тот факт, что он когда-либо отправлял поручение по
электронной почте. Разумеется, банк может предъявить электронное поручение, но
клиент может заявить, что банк его подделал с целью получения комиссионных. Как
судья узнает, кто из них говорит правду?
690
Глава 9. Безопасность
Цифровые подписи позволяют подписывать электронные сообщения и другие цифровые
документы таким образом, чтобы позже отправитель не смог от них отказаться. Один из
распространенных способов заключается в первоначальном пропуске документа через
односторонний криптографический алгоритм хэширования, который очень трудно
инвертировать. Хэш-функция обычно выдает результат фиксированной длины, не за-
висящий от размера исходного документа. Самой популярной хэш-функцией является
SHA-1
(Secure Hash Algorithm), производящая 20-байтный результат (NIST, 1995). Но-
вейшие версии SHA-1 — SHA-256 и SHA-512 — производят 32- и 64-байтный результат
соответственно, но пока они не получили такого же широкого распространения.
Следующий шаг предполагает использование описанного ранее шифрования с откры-
тым ключом. Владелец документа применяет свой закрытый ключ к хэшу, чтобы полу-
чить D(hash). Это значение, получившее название сигнатурного блока (signature block),
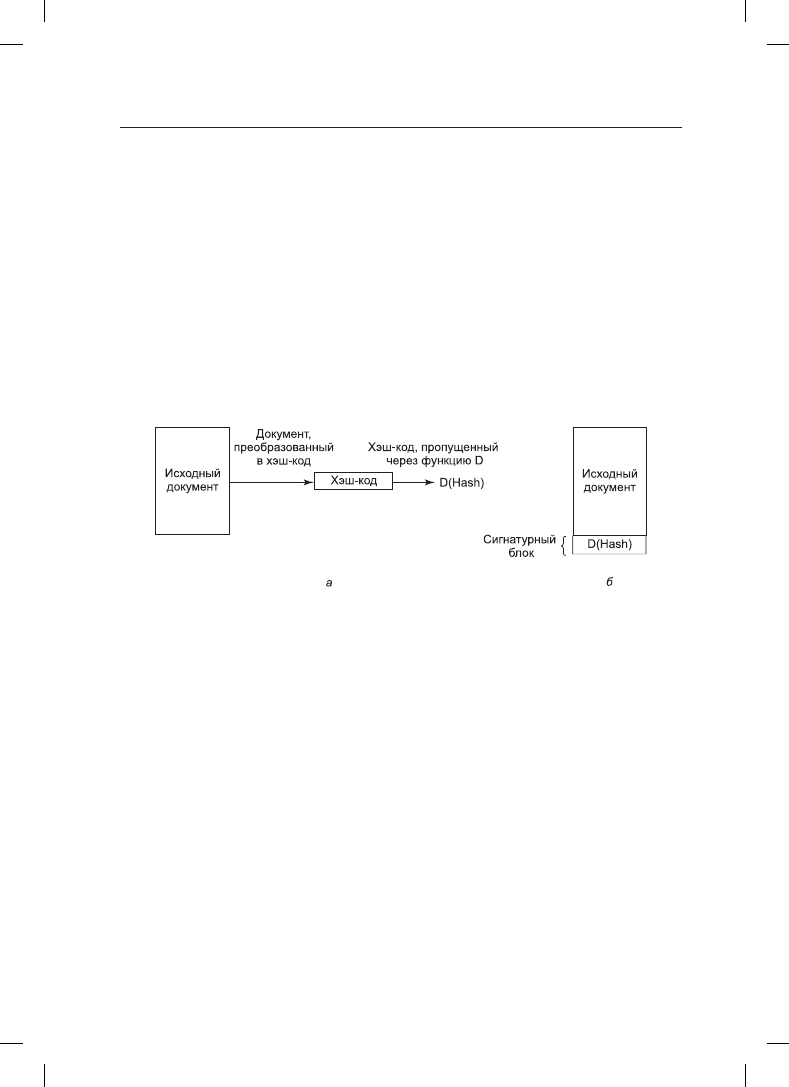
прикрепляется к документу и отправляется получателю (рис. 9.14). Иногда применение
функции D к хэшу называют дешифровкой хэша, но на самом деле это не дешифровка,
поскольку хэш не был зашифрован. Это просто математическое преобразование хэша.
Рис. 9.14. а — вычисление сигнатурного блока; б — то, что приходит получателю
При получении документа и хэша получатель сначала вычисляет хэш документа, ис-
пользуя заранее согласованный алгоритм SHA-1 или оговоренную криптографическую
хэш-функцию. Затем получатель применяет к сигнатурному блоку открытый ключ
отправителя, чтобы получить E(D(hash)). В результате этого он путем взаимоуничто-
жения «зашифровывает» расшифрованный хэш и получает его в прежнем виде. Если
вычисленный хэш не соответствует хэшу из сигнатурного блока, значит, документ,
сигнатурный блок или и то и другое были подделаны (или случайно изменены). Цен-
ность такой схемы заключается в том, что довольно медленное шифрование с откры-
тым ключом применяется в ней только в отношении хэша, представляющего собой
сравнительно небольшую часть данных. Следует учесть, что данный метод работает
только в том случае, если для всех x
E(D(x)) = x.
Наличие этого свойства у всех функций шифрования заранее не гарантируется, по-
скольку все, что от них изначально требовалось, — это соблюдение условия
D(E(x)) = x,
где E — функция шифрования, а D — функция дешифрования. Чтобы получить еще
и свойство подписи, порядок их применения не должен играть никакой роли, то есть