Добавлен: 30.10.2018
Просмотров: 364
Скачиваний: 10
Лабораторная работа № 4
Тема: Решение алгебраических уравнений и систем
с помощью надстройки Поиск решения
Краткие теоретические сведения:
Надстройка Поиск решения является инструментом оптимизации, с ее помощью можно найти оптимальное или заданное значение некоторой ячейки (она называется целевой) путем подбора значений нескольких ячеек (они называются изменяемыми), удовлетворив нескольким граничным условиям.
Целевая ячейка – та, для которой нужно найти максимальное, минимальное или заданное значения. Она должна содержать формулу, зависящую от изменяемых ячеек (прямо или косвенно). Пока не будет найдено решение, программа подбирает значения изменяемых ячеек.
Изменяемые ячейки – те, от которых зависит значение целевой ячейки.
Процедуру поиска решений можно использовать, например, для решения алгебраических уравнений и систем алгебраических уравнений.
-
Решение алгебраических уравнений.
Для нахождения корней уравнения алгоритм действий следующий:
-
Уравнение приводится к форме, в которой все его члены перенесены в одну часть, а в другой части находится ноль, или в одну часть уравнения переносится свободный член.
-
В изменяемой ячейке задается первоначальное значение переменной (начальное приближение корня уравнения).
-
В другую, целевую ячейку, вводится формула для расчета части уравнения, содержащей искомое значение переменной (искомое значение записывается через адрес изменяемой ячейки).
-
Вызывается средство Поиск решения - Сервис \ Поиск решения…, и в диалоговом окне Поиск решения задаются нужные критерии поиска.
-
После нажатия кнопки Выполнить будет найдено решение, ближайшее к выбранному начальному приближению корня уравнения.
Пример:
Используя надстройку Поиск решения
решить уравнение
![]() .
.
Решение:
-
Приведем уравнение к форме, когда все его члены перенесены в одну часть:
![]() или
или
![]()
Подходят обе версии. Рассмотрим первую из них.
-
На рабочем листе Excel введем исходные данные в изменяемую и целевую ячейки (рис.1).
-
Вызовем надстройку Поиск решения и в одноименном диалоговом окне зададим критерии поиска (рис. 2).
После нажатия кнопки Выполнить найдено решение, ближайшее к выбранному начальному приближению одного из корней. Результат помещен в изменяемую ячейку (рис. 3).
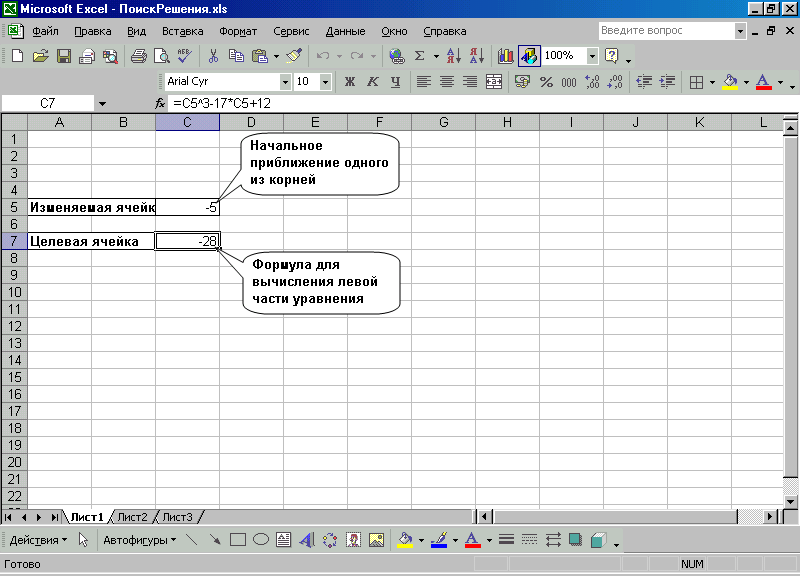
Рис. 1. Исходные данные для решения уравнения
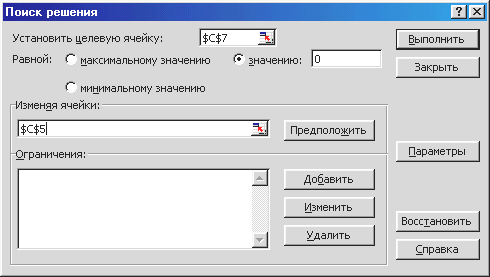
Рис. 2. Критерии поиска для решения уравнения
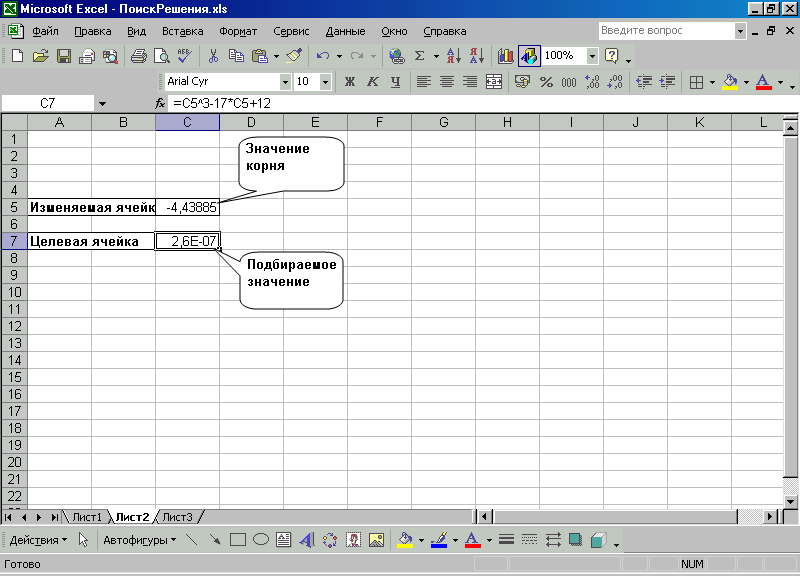
Рис. 3. . Результат выполнения процедуры поиска решения уравнения
Для нахождения двух других корней уравнения необходимо задать начальные приближения для них, например: 0 и 3,5.
-
Решение системы алгебраических уравнений.
При решении системы алгебраических уравнений находятся корни одного из уравнений (как описано выше), а остальные уравнения выступают в качестве ограничений при поиске решения выбранного уравнения.
Для нахождения корней системы уравнения алгоритм действий следующий:
-
Уравнения приводятся к форме, когда все его свободный члены переносятся в одну часть, например в правую.
-
В ячейки рабочего листа вводятся следующие группы данных:
-
начальные значения переменных (изменяемые ячейки);
-
коэффициенты системы уравнений;
-
свободные члены уравнений;
-
формулы для вычисления, например левых частей уравнений, содержащих искомые значения переменных (искомые значения записываются через абсолютные адреса изменяемых ячеек, а коэффициенты через относительные адреса ячеек, содержащих значения коэффициентов).
-
Вызывается средство Поиск решения и в одноименном диалоговом окне задаются нужные критерии поиска:
-
Установить целевую ячейку – указывается абсолютный адрес любой из ячеек, содержащих формулу для вычисления левой части уравнения (назовем это уравнение «основным»);
-
Равной: значению: - вводится значение свободного члена «основного» уравнения (это значение должно быть достигнуто в результате поиска решения);
-
Изменяя ячейки: - указывается абсолютный диапазон ячеек с начальными значениями переменных (диапазон изменяемых ячеек).
-
Ограничения: - для каждого уравнения, кроме «основного», вводится равенство абсолютного адреса ячейки, содержащей формулу для вычисления левой части, и абсолютного адреса ячейки, содержащего свободный член этого уравнения.
-
После нажатия кнопки Выполнить будет найдено решение, ближайшее к выбранным начальным приближениям корней уравнений.
Пример: Используя надстройку Поиск решения решить следующую систему уравнений
![]()
Решение:
-
Все уравнения уже приведены к форме, когда их свободные члены находятся в одной части.
-
Подготовим исходные данные на рабочем листе Excel (рис. 4).
-
Вызовем надстройку Поиск решения и в одноименном диалоговом окне зададим критерии поиска (рис. 5).
После нажатия кнопки Выполнить найдены корни системы уравнений. Результат помещен в изменяемые ячейки (рис. 6).
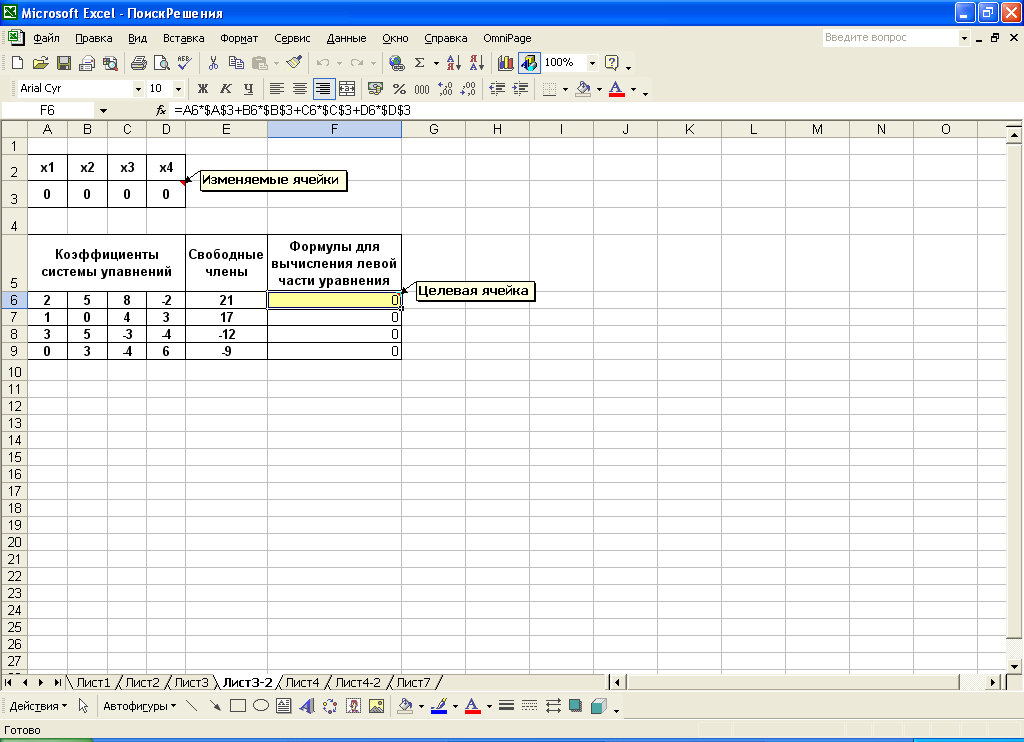
Рис. 4. Исходные данные для решения системы уравнений
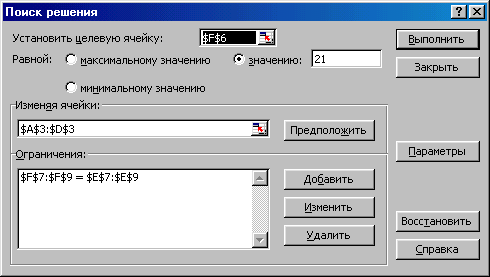
Рис. 5. Критерии поиска для решения системы уравнений
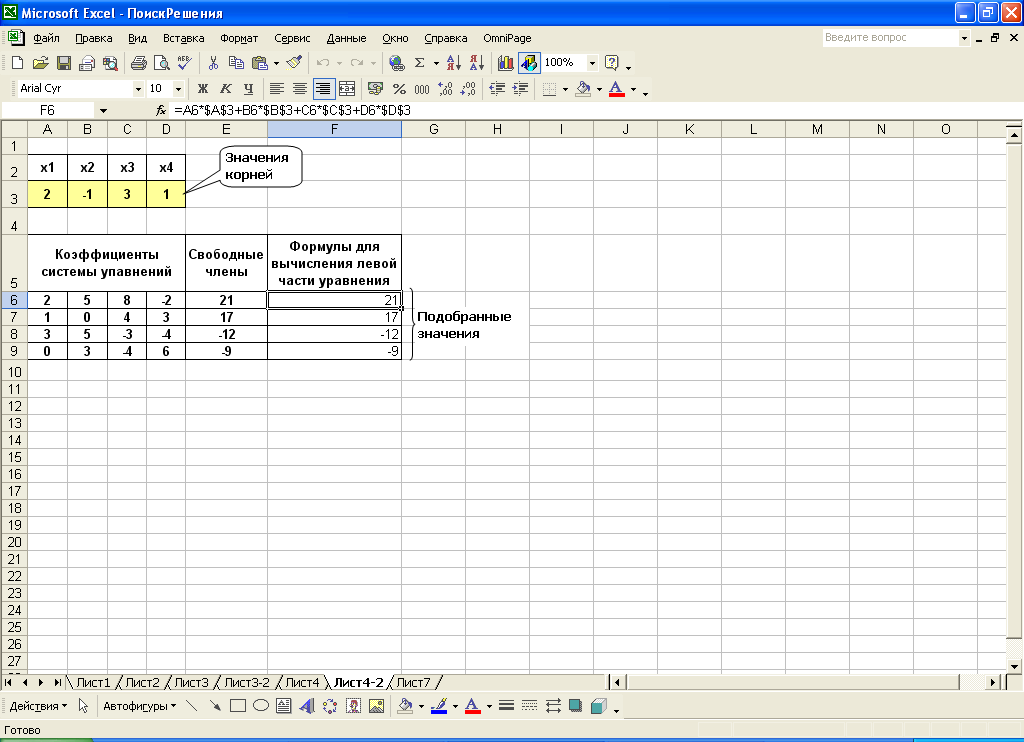
Рис. 6. Результат выполнения процедуры поиска решения системы уравнений
Задание:
Используя надстройку Поиск решения найдите корни:
-
Линейных уравнений:
а)
![]() ;
б)
;
б)
![]() .
.
-
Нелинейных уравнений:
а)
![]()
Рассмотрите следующие начальные приближения корней: 0,5; 2,5; 6,5.
б)
![]()
Рассмотрите следующие начальные приближения корней: 0; 0,5; 2.
-
Систем линейных уравнений:
![]()
а)
![]()
б)