Лабораторная работа Excel-1

Численное решение уравнений с помощью электронных таблиц Excel

Примером одного из самых удачных использований электронных таблиц при решении математических задач является определение нулей функции (или корней уравнений), что имеет фундаментальное значение в прикладной математике.

Использование возможностей Exсel позволяет обучаемым ценой минимальных усилий познакомится с численными методами решения уравнений и пронаблюдать непосредственно процесс их решений.

В основе метода, который используется в предлагаемом примере, лежит теорема Больцано, которая гласит:

Если функция F, определенная в интервале [a, b], имеет значения F[a] и F[b] с противоположными знаками, то в интервале [a, b] существует такое значение x, для которого F(x)=0.

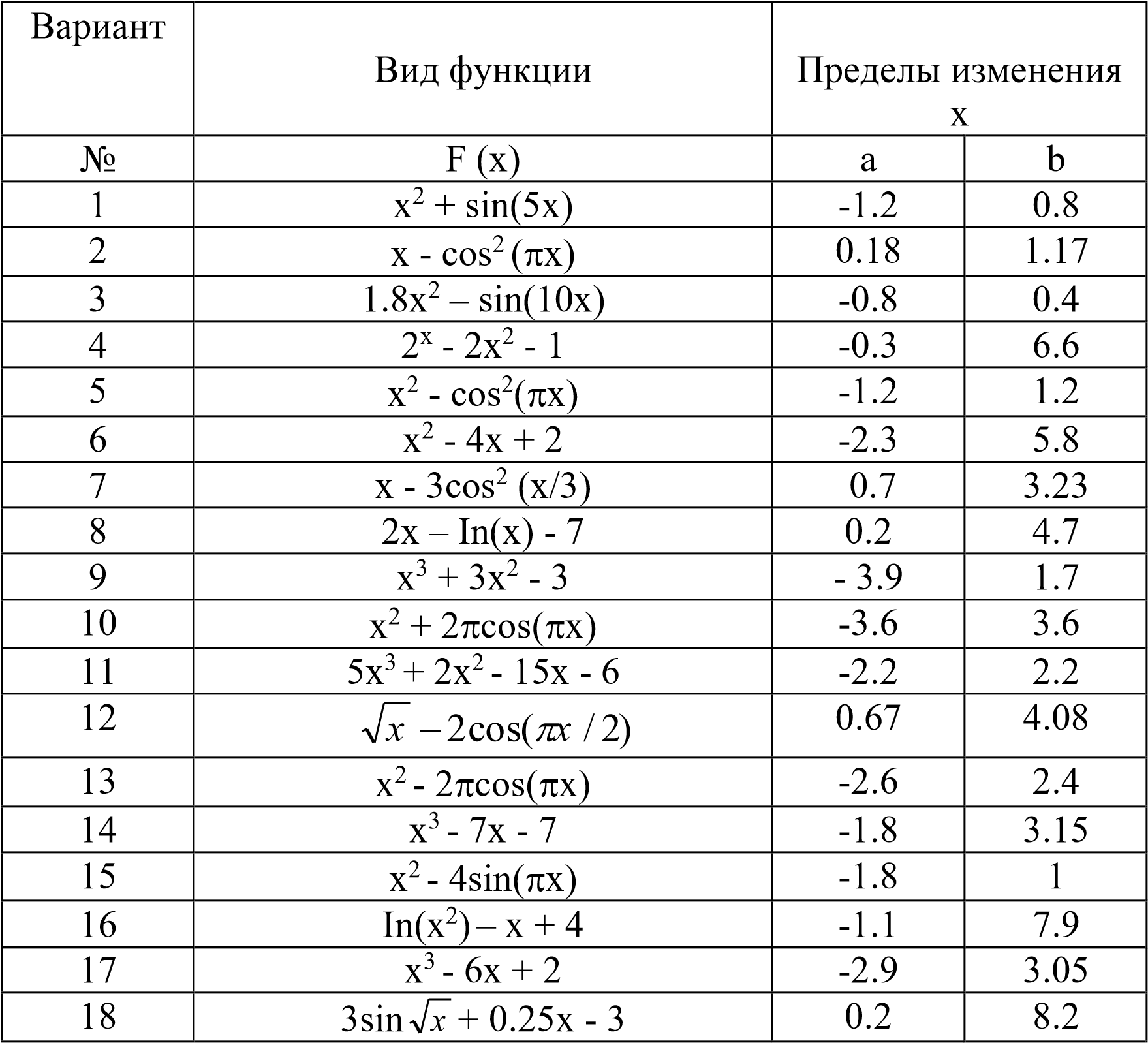
Данная теорема лежит в основе приближенного вычисления корней уравнений с заданной точностью. Рассмотрим пример. Пусть необходимо решить следующее уравнение: x³ + 5 = 3х².

Оно может быть записано в виде:

x³ - 3х² + 5 = 0.

Мы будем аппроксимировать функцию

F = x³ - 3х² + 5

до решения F(х)=0 с заданной точностью (возьмем для примера EPS = 10^-5 ).

Сначала необходимо определить интервал [a, b], на котором функция меняет свой знак, т.е. F(a)*F(b)=0. Это нетрудно сделать при помощи табулирования функции. Для данного примера в качестве начального интервала выбирается [-3, 3].

Полученный интервал [a, b] делится на 10, и определяется новый подинтервал, в котором функция меняет свой знак. Процесс деления повторяется, пока не будет получено решение F(х) = 0 с заданной точностью. Этот подход является методом последовательного приближения путем деления интервала на 10.

Алгоритм решения поставленной задачи может быть представлен следующими шагами:

1. Создайте заголовок и опишите функцию F(x).

2. Заполните шапку таблицы названиями столбцов Х и F.

3. Занесите в первую строку столбца для Х начальное значение аргумента, т.е. -3.

4. Запишите в первую строку столбца для F формулу вычисления функции:

=B6^3-3*B6^2+5 5. Занесите в последнюю строку столбца для Х конечное значение аргумента, т.е. 3.

6. Запишите в ячейку E6 заданную точность EPS, равную 0,0001.

7. Выберите ячейку для шага изменения Х, например F6, и запишите в нее формулу: =(B6-B16)/10 8. Запишите в ячейку B7 следующую формулу, вычисляющую изменение аргумента с шагом STEP:

=B6-F$6 9. Используя функцию автозаполнения, занесите в столбец для Х значения аргументов до ячейки B15с шагом изменения STEP .

10. Заполните столбец, предназначенный для функции F, скопировав формулу из первой строки столбца C6.

В результате выполненых действий вы получите таблицу, представленную на рис.1

10. Найдите подинтервал, в котором функция F меняет свой знак (на рис.1 соответствующие ячейки таблицы выделены желтым цветом).

Для наглядности надо построить график функции по данным полученной таблицы, на котором сразу видно, где функция меняет знак, переходя через ноль (рис.2).

---

10. Скопируйте значение Х с ближайшем к нулю отрицательным значением F в первую строку столбца для Х, а с ближайшим положительным — в последнюю строку столбца для Х. Обратите внимание на то, как изменится содержимое ячейки F6 — шаг уменьшится в 10 раз (рис.3).

Если заданная точность вычисления Х не достигнута, необходимо вернуться к пункту 8 и повторить всю процедуру.

В таблице также предусмотрена ячейка для конечного результата — G10 и вспомогательная ячейка G13 с формулой подсказки, необходима ли следующая итерация, т.е. достигнута ли заданная точность вычисления функции F(x):

=ЕСЛИ(ABS(C6)<=$E$6;“НЕТ”;“ДА”)

	A	B	C	D	E	F	G	H
1
2		Численное решение уравнения
3			F(x)=x3-3*x2+5
4
5		X	F		EPS	STEP
6		-3	-49		1E-05	-0,6
7		-2,4	-26,104
8		-1,8	-10,552
9		-1,2	-1,048
10		-0,6	3,704		Результат:		-3,00
11		0	5
12		0,6	4,136
13		1,2	2,408		Продолжаем:		ДА
14		1,8	1,112
15		2,4	1,544
16		3	5

Рис. 1. Первая итерация.

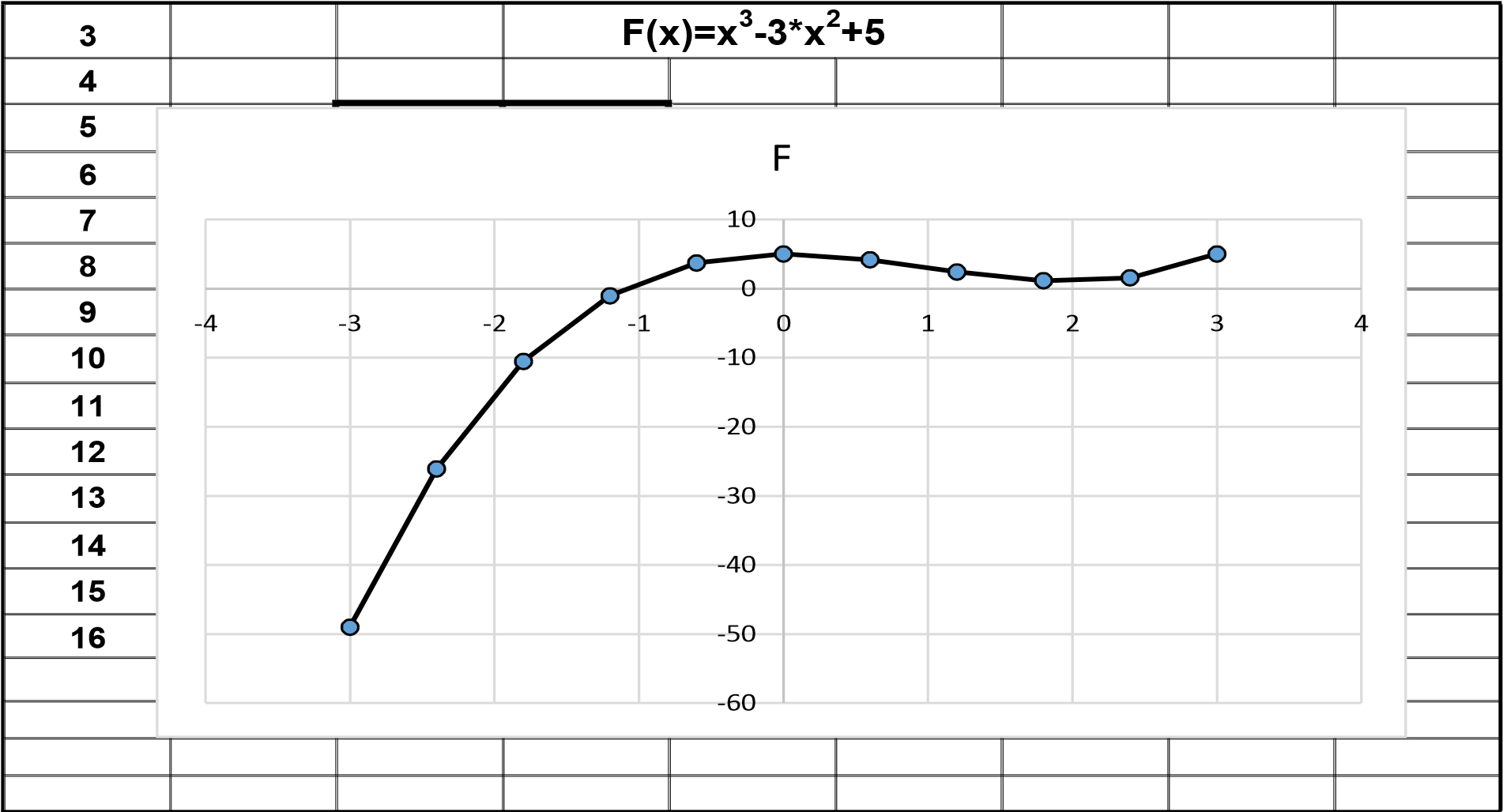
Рис.2. График функции

3			F(x)=x3-3*x2+5
4
5		X	F		EPS	STEP
6		-1,2	-1,048		0,0001	-0,06
7		-1,14	-0,3803
8		-1,08	0,2411
9		-1,02	0,8176
10		-0,96	1,3505		Результат:			-1,2
11		-0,9	1,841
12		-0,84	2,2905
13		-0,78	2,7002		Продолжаем:		ДА
14		-0,72	3,0716
15		-0,66	3,4057
16		-0,6	3,704
		6

---

Рис. 3. Вторая итерация.

	A	B	C	D	E	F	G
1
2			Численное решение уравнения
3			F(x)=x3-3*x2+5
4
5		X	F		EPS	STEP
6		-1,10381	-6,7807E-05		0,0001	-1E-06
7		-1,10381	-5,7529E-05
8		-1,10381	-4,7251E-05
9		-1,10381	-3,6973E-05
10		-1,10381	-2,6695E-05		Результат:			-1,10381
11		-1,10381	-1,6417E-05
12		-1,1038	-6,1387E-06
13		-1,1038	4,1393E-06		Продолжаем:			НЕТ
14		-1,1038	1,4417E-05
15		-1,1038	2,4695E-05
16		-1,1038	3,4973E-05

Рис. 4. Последняя итерация.

Данный пример решается за 6 итераций. Последнее значение Х, обеспечивающее приближение функции F(x) к нулю с заданной точностью EPS = 10^-4, записано в первую строку столбца для Х и в ячейку для результата G10 таблицы (рис.4).

Задание

• Построить график функции в соответствии со своим вариантом, пользуясь мастером диаграмм (выбрать точечную).

• Найти корни уравнения в соответствии с вариантом.

Номер варианта выбирается по сумме двух последних цифр зачетной книжки.

---

Смотрите также файлы

• Контрольная работа ИТ в управлении.DOC

• Приложение V.pdf

• Приложение B.pdf

• Kурсовая работа по ТИП.doc

• Программа и задания Ит в ПД.doc