Файл: ЛР Специальные главы математики.pdf

16 

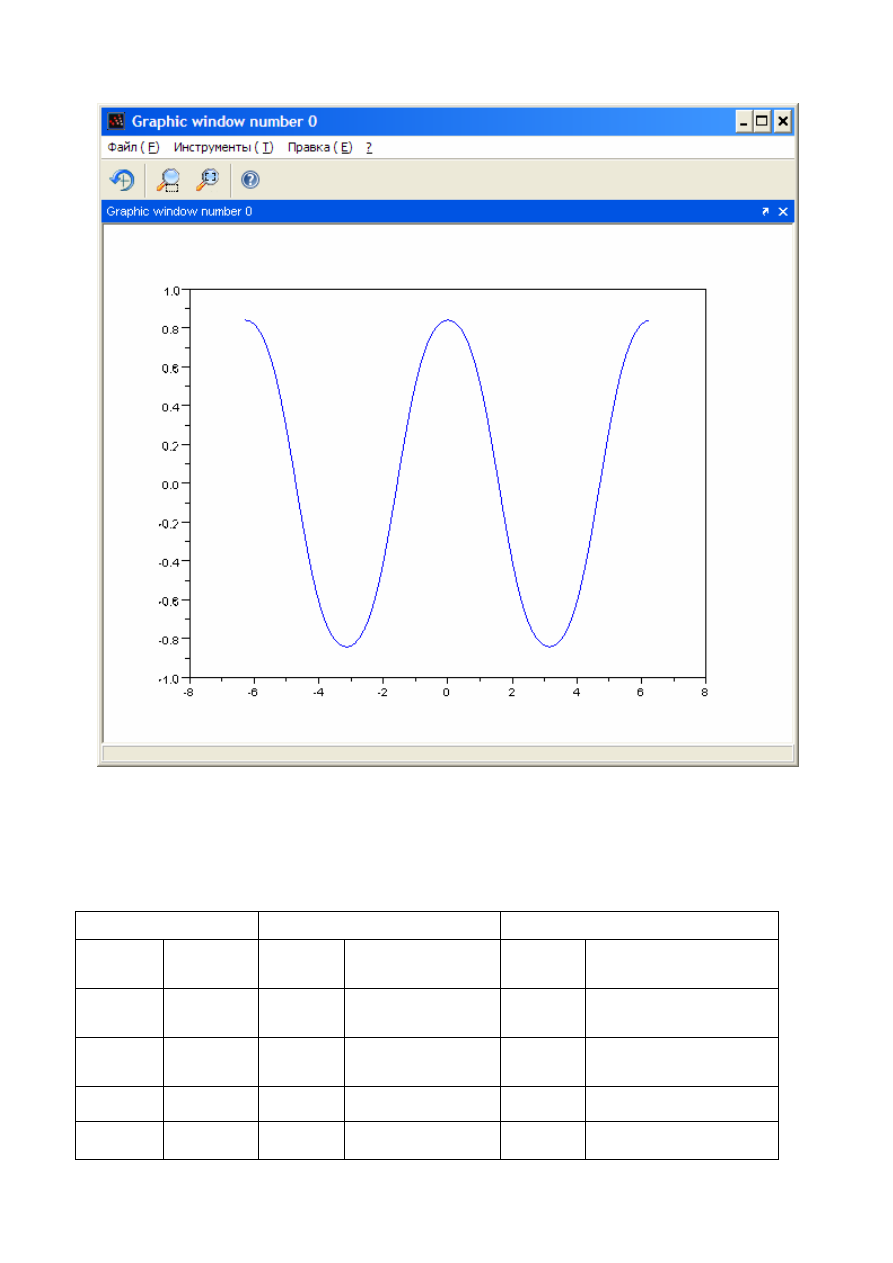
Рис. 7 

Рис. 8. Построенный график функции 

Форматирования графика. В Scilab внешний вид графика можно изменять, 

используя дополнительный параметр функции plot: строку из трех символов, 

заключенных в апострофы. Эти символы задают цвет линии, тип маркера и тип 

линии соответственно (табл. 2). 

Табл. 2. Некоторые символы для задания внешнего вида функции 

Цвет 

Маркер 

Линия 

Симво

л 

Цвет 

Симво

л 

Тип маркера 

Симво

л 

Тип линии 

r 

красны

й 

* 

звездочка 

- 

сплошная 

g 

зелены

й 

s 

квадрат 

-.. 

пунктир две точки 

b 

синий 

d 

ромб 

-. 

пунктир точка 

k 

черный 

о 

кружок 

- - 

пунктирная 

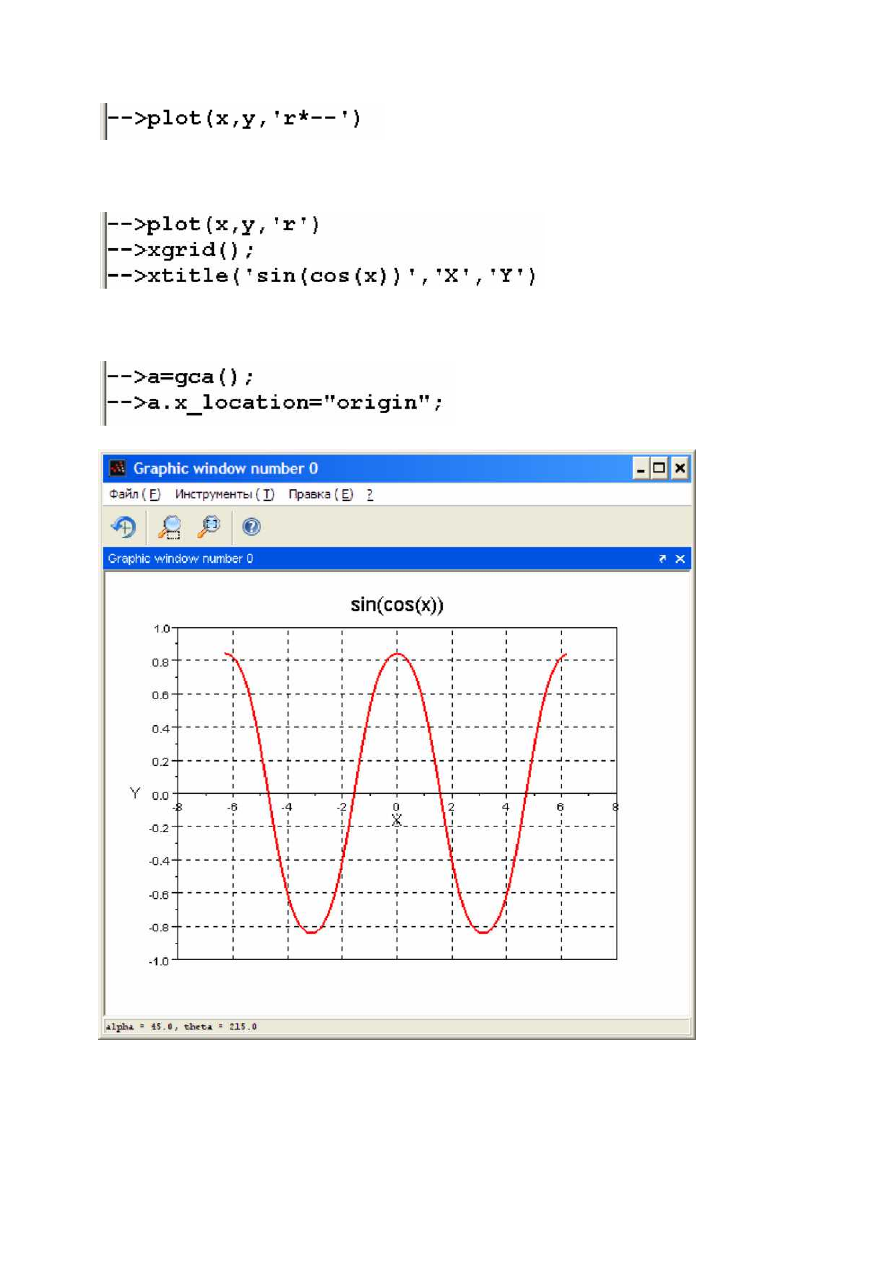
Построение пунктирного графика красного цвета с маркерами в виде *: 

17 

Внешний вид графика можно также изменять, используя функцию xgrid(), 

чтобы задать линии сетки и функцию xtitle(), чтобы задать название графика и его 

осей: 

Расположение осей графика можно изменить, получив доступ к параметрам 

осей с помощью команды gca() и используя соответствующие команды. 

Например, для перемещения оси X в начало координат следует использовать: 

На рис. 9 приведен отформатированный график. 

Рис. 9. Отформатированный график 

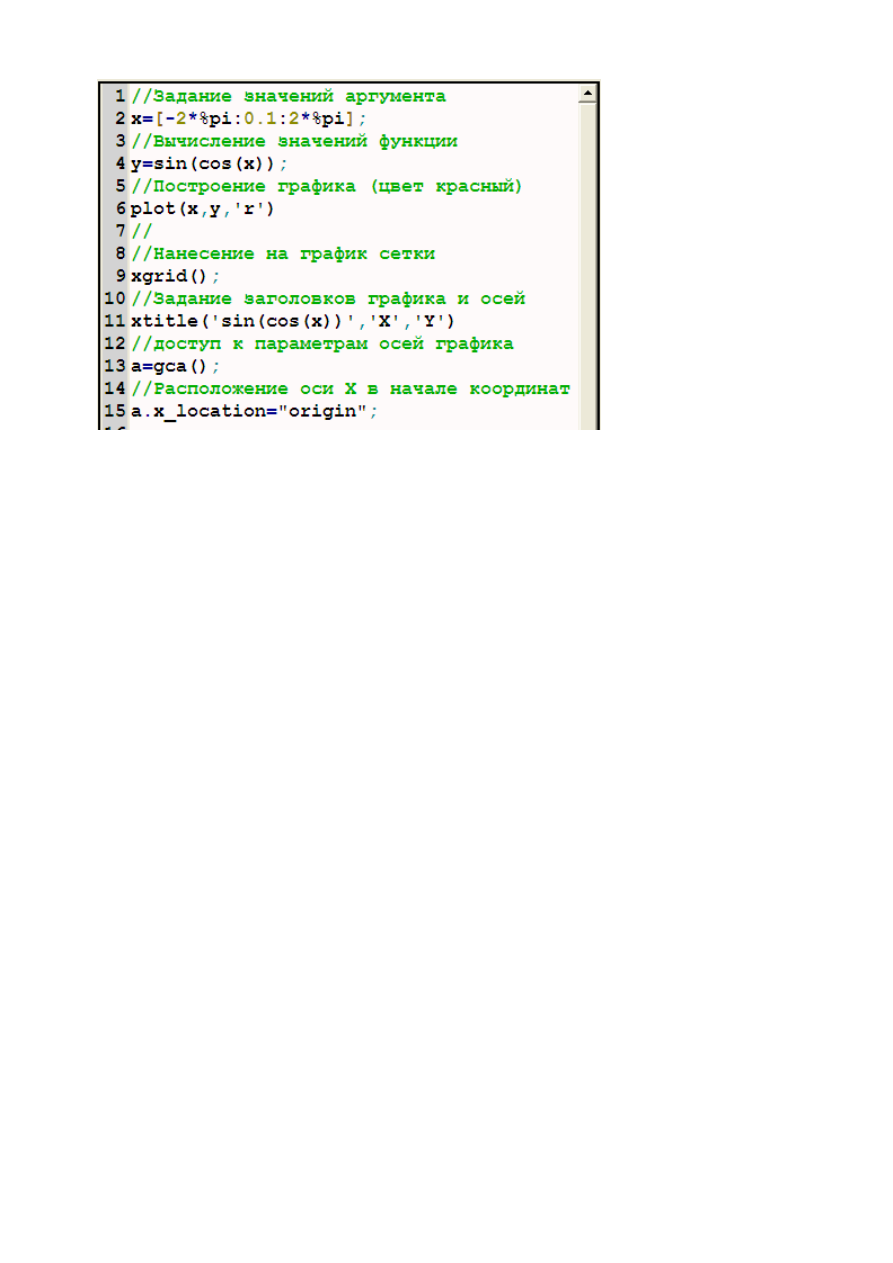
На рис. 10 приведен файл-сценарий построения графика рассматриваемой 

функции. 

18 

Рис. 10 Файл-сценарий построения графика рассматриваемой функции. 
 

Лабораторная работа №2 

Тема:  Решение нелинейных уравнений и систем. 

 
1. 

Цель работы 

Использование методов решения нелинейных уравнений и систем для решения 

конкретных производственных задач.  

2. 

Учебные вопросы, подлежащие рассмотрению: 

− 

Отделение корней уравнения. 

− 

Решение нелинейных уравнений:  

 

метод половинного деления,  

 

метод простых итераций,  

 

метод Ньютона. 

3. 

Порядок выполнения работы 

Задание 1. 

Вычислить наименьший положительный корень заданного уравнения с 

точностью ε=10

-3

. Работу провести в три этапа: 

1) Провести графическое отделение корней уравнения. 

2) Сузить отрезок, полученный графическим способом до отрезка длиной 0.1. 

3) Вычислить приближенное решение методом половинного деления. 

По итогам выполнения заданий представить корень уравнения, вычисленный с 

указанной точностью. 

Номер варианта соответствует порядковому номеру в списке. 

Задание 2. 

Найти решение уравнения с точностью ε=10

-4

, используя метод простой 

итерации и один из методов Ньютона. 

Номер варианта соответствует порядковому номеру в списке. 

Исполнение: Освоить реализацию итерационных процессов с использованием 

логических функций в MS Excel. 

19 

Оценка: Использование инструментальных пакетов для решения 

трансцендентных уравнений. 

Методические указания 

Краткая теория метода половинного деления 

Многие проблемы физики, строительной и технической механики, техники и 

других областей приводят к задаче нахождения корней нелинейного уравнения с 

одной переменной. В общем случае нелинейное уравнение можно записать в виде 

F(x) =0,                                                                 (1) 

где функция F(x) определена и непрерывна на конечном или бесконечном 

интервале [a, b]. Примерами трансцендентных уравнений являются уравнения 
x

2

 - sin x= 0;      tg(x- 6) =3

x

. 

Определение 1. Число x * , такое, что F( x*)=0 называется корнем уравнения 

(1). 

Для подавляющего числа нелинейных уравнений вида (1) невозможно (или 

очень сложно) решить задачу нахождения корней уравнения аналитическими 

методами. Поэтому на практике такие уравнения решаются численными 

методами, вместо точного решения x* вычисляется приближенное решение. 

Определение 2. Число  , такое, что 

называется приближенным 

решением уравнения (1), найденным с точностью ε >0. 

Задача численного нахождения приближенных корней состоит из двух этапов: 

отделение корней, то есть нахождение достаточно малого интервала (a, b) , в 

котором содержится один корень уравнения (1), и уточнение корня, т.е. 

вычисление приближенного решения с необходимой точностью. 

Графическое отделение корней. 

Для того чтобы провести графическое отделение корней, надо построить 

график функции y =F(x) и визуально определить интервал, на котором находится 

ровно один корень уравнения. 

Уточнение корня методом половинного деления. 

Основная идея нахождения приближенного решения заключается в 

сокращении первоначального интервала, определенного при графическом 

отделении, до интервала длиной 2 ε. После того, как удалось сократить интервал 

до заданной величины, можно определить   =(a +b) / 2. В этом случае условие 

выполнено. 

В методе половинного деления сокращение интервала происходит делением 

отрезка [a, b] пополам и выбора той из половин, которой принадлежит искомый 

корень уравнения. 

Итак, алгоритм численного решения уравнения (1) методом половинного 

деления заключается в выполнении следующих шагов: 

1. определить начальный отрезок [a, b]; 

2. найти точку с – середину отрезка [a, b], c = (a +b) / 2; 

3. проверить, какому из отрезков [a, c] или [c, b] принадлежит корень. Легко 

видеть, что проверка выполняется так: 

если f (a)* f (c)<,0, то корень принадлежит отрезка [a, c] и в дальнейшем надо 

положить b =c, в противном случае корень принадлежит отрезку [c, b] и 

следует положить a =c; 

20 

4. если длина отрезка [a, b] больше 2 , то перейти к пункту 2; 

5. закончить вычисления, положив   =(a +b) / 2. 

Теория электронных таблиц 

Для реализации данного алгоритма необходимо воспользоваться логическими 

функциями. Логические функции предназначены для проверки выполнения 

условия или для проверки нескольких условий. В отличие от математических 

функций, при проведении вычислений с логическими функциями мы оперируем 

понятиями ИСТИНА и ЛОЖЬ. 

В общем виде функция, позволяющая учесть при вычислениях условия 

выглядит так: 

ЕСЛИ(логическое выражение; значение1; значение2) 

логическое выражение – это выражение, принимающее значения ИСТИНА или 

ЛОЖЬ. Например, С15=1 – это логическое выражение. Если значение в ячейке 

С15 равно 1, то выражение принимает значение ИСТИНА, иначе – ЛОЖЬ. 

Значение1 – это значение, которое заносится в ячейку, если логическое 

выражение равно ИСТИНА; значение2 – это значение, которое заносится в 

ячейку, если логическое выражение равно ЛОЖЬ. 

До семи функций ЕСЛИ могут быть вложены друг в друга в качестве значений 

аргументов значение1 и значение2 для конструирования более сложных проверок. 

Если любой из аргументов функции ЕСЛИ является массивом, все элементы 

массива вычисляются при выполнении функции ЕСЛИ. 

Microsoft Excel предлагает дополнительные функции, которые можно 

применять для анализа данных с использованием условий. Например, для 

вычисления числа появлений текстовой строки или числа в диапазоне ячеек 

используется функция СЧЁТЕСЛИ. Для вычисления суммы значений, 

попадающих в интервал, заданный текстовой строкой или числами, используется 

функция СУММАЕСЛИ. 

Для записи логических выражений (условий) служат стандартные операции 

сравнения: = (равно), > (больше), < (меньше), >= (больше или равно), <= 

(меньше или равно), <> (не равно). Если требуется записать более сложные 

условия, включающие в себя несколько простых условий, то приходится 

применять такие логические функции, как И, ИЛИ, НЕ. 

И(логическое выражение1; логическое выражение2; ...) 

Функция И будет иметь значение ИСТИНА, если все логические выражения, 

перечисленные в скобках, истинны. В противном случае результатом функции 

И будет значение ЛОЖЬ. Всего можно указать до 30 различных условий. 

ИЛИ(логическое выражение1; логическое выражение2; ...) 

Функция ИЛИ возвращает значение ИСТИНА, если хотя бы один из 

аргументов имеет значение ИСТИНА и возвращает ЛОЖЬ, если все аргументы 

имеют значение ЛОЖЬ. 

НЕ(логическое выражение) 

Если логическое выражение имеет значение ЛОЖЬ, то функция НЕ возвращает 

значение ИСТИНА; если логическое выражение имеет значение ИСТИНА, то 

функция НЕ возвращает значение ЛОЖЬ. 

Методика выполнения