Файл: Контрольная работа по дисциплине Основы теории надежности Барнаул 2019 г. Содержание зач кн 7.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 56
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Коэффициент вариации - это относительная характеристика случайной величины, используется при выборе теоретического закона распределения.
Идентификация случайных последовательностей, нестационарных случайных процессов и их производных по первым реализациям динамического ряда обусловливает необходимость введения в рассмотрение выборочного распределения коэффициента вариации. Коэффициентом вариации (коэффициентом изменчивости выборки) является отношение
где
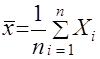 и
и 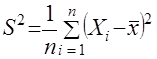 – среднее значение и дисперсия выборки соответственно.
– среднее значение и дисперсия выборки соответственно.Гауссово распределение не обладает тем свойством, что случайная величина может принимать только положительные значения, однако если
В этом случае
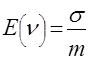 ,
, 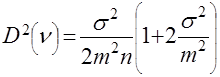 , (14)
, (14)где
Величина
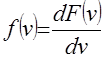 .
.Не нарушая общности рассуждений и с целью использования зависимости (2) определим плотность распределения величины, обратной выборочному коэффициенту вариации
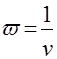 , для выборки
, для выборки
Если каждая из независимых величин
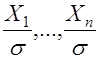 независимы и нормальны (0,1). Таким образом, плотность вероятности величины
независимы и нормальны (0,1). Таким образом, плотность вероятности величины 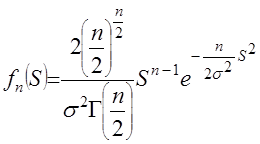 . (15)
. (15)Среднее арифметическое
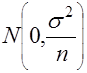 .
.Поэтому можно показать, что плотность
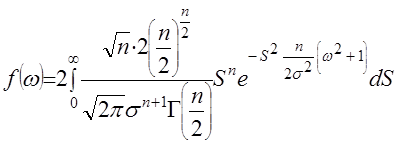 . (16)
. (16)При
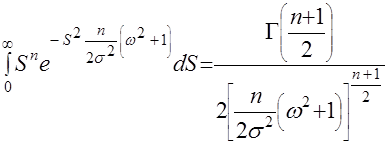 (17)
(17)При
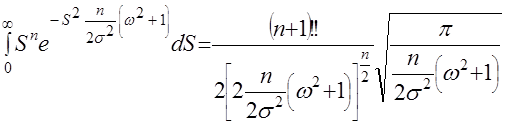 . (18)
. (18)После соответствующих преобразований плотность распределения величины
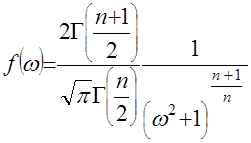 . (19)
. (19)Учитывая, что
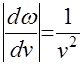 , получаем следующий результат.
, получаем следующий результат.Теорема 5. Пусть
плотность распределения выборочного коэффициента вариации
имеет вид
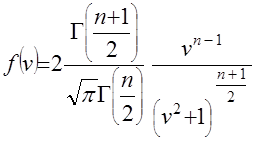 . (20)
. (20)Теоретический закон распределения (ТЗР) выражает общий характер изменения показателя надежности и исключает частные отклонения, связанные с недостатком первичной информации, т.е. ТЗР характеризует генеральную совокупность. Опытное распределение имеет частные особенности, которые должны быть исключены при переносе характеристик опытного распределения на генеральную совокупность.
Процесс замены опытных закономерностей теоретическими называется выравнивание опытной информации.
Каждый ТЗР характеризуется двумя функциями:
f(t) - дифференциальная функция;
F(t) - интегральная функция.
Применительно к показателям надежности машин, эксплуатируемых в сельском хозяйстве, в подавляющем большинстве случаев используется закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ).
Выбор теоретического закона производится исходя из следующих признаков:
По величине коэффициента вариации:
-
если V < 0,3 - выбирается ЗНР; -
если 0,3 < V < 0,5 - выбирается ЗНР или ЗРВ; -
если V > 0,5 - выбирается ЗРВ.
По области применения.
ЗНР применяется, как правило при определении характеристик рассеивания:
-
ресурсов и сроков службы машин и агрегатов; -
времени и стоимости восстановления работоспособности машин; -
наработка на ресурсный отказ; -
ошибок измерений размеров деталей.
б) ЗРВ применяется, как правило, при определении:
-
ресурсов и сроков службы отдельных деталей и сопряжений; -
доремонтных и межремонтных ресурсов тех элементов машин, отказы которых вызваны выходом из строя одной и той же детали; -
информации по износам деталей.
Здесь применим закон нормального распределения и закон распределения Вейбулла.
Закон нормального распределения (ЗНР)
Отличительной особенностью ЗНР является симметричное рассеивание частных значений относительного среднего.
_________________________________________
3 Обеспечение надежности сложных технических систем [Электронный ресурс]: учебник/А.Н.Дорохов – Спб: Лань, 2010, 352 с.
Список литературы
-
Зубарев Ю.Н. Основы надежности машин и сложных систем Учебник для ВУЗов. М.Колос 2017 г. - 221стр. -
Надежность и ремонт машин. В.В Курчаткин, Н.Ф. Тельнов, К.А. Ачкасов и др. Под.ред. В.В Курчаткина – М:Колос, 2000 г. -
Обеспечение надежности сложных технических систем [Электронный ресурс]: учебник/А.Н.Дорохов – Спб: Лань, 2010, 352 с.