Файл: Контрольная работа учебнометодическое пособие Новосибирск 2021.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 185
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Для вычисления коэффициентов переходов применим ф. 13-15, при этом, чтобы получить единственное решение для замкнутой СеМО, присвоим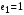 :
:
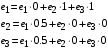
Решение системы: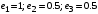 .
.
Далее рекуррентно для различных значений k (количество заявок в СеМО) вычисляем с учётом начальных условий: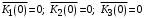 .
.
– для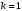
1. Среднее время реакции в узлах:
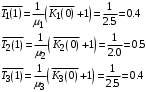 .
.
2. Среднее время реакции в СеМО:
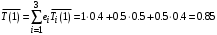 .
.
3. Пропускная способность СеМО:
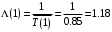 .
.
4. Интенсивности потоков заявок в узлы:
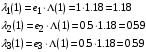 .
.
5. Среднее количество заявок в узлах:
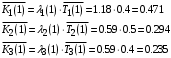 .
.
– для к=К=2
1. Среднее время реакции в узлах:
 .
.
2. Среднее время реакции в СеМО:
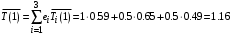 .
.
3. Пропускная способность СеМО:
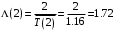 .
.
4. Интенсивности потоков заявок в узлы:
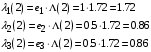 .
.
5. Среднее количество заявок в узлах:
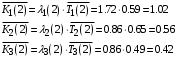 .
.
По ф. (27)–(32) можно получить остальные характеристики (узловые и сетевые) моделируемой системы.
П римечание 2: каналы, связывающие сетевые устройства, не моделируются узлами СеМО, но количество прилегающих к каждому устройству линий связи должно соответствовать количеству обслуживающих приборов (каналов) в соответствующей объекту системе массового обслуживания.
римечание 2: каналы, связывающие сетевые устройства, не моделируются узлами СеМО, но количество прилегающих к каждому устройству линий связи должно соответствовать количеству обслуживающих приборов (каналов) в соответствующей объекту системе массового обслуживания.
Получить вероятностно-временные характеристики сети в зависимости от количества заявок в СеМО, сетевые характеристики:
Отобразить зависимости, полученные в пп. 3-4 графически.
Для расчётов использовать программные пакеты инженерной математики, такие как Mathcad, Matlab, SMathStudio (последний является бесплатно распространяемым).
Сдать контрольную работу преподавателю на проверку (отчёт в формате .doc, .docx, .pdf и обязательно файл(ы) с расчётами).
По результатам проверки внести необходимые исправления и защитить работу.
Топологии сетей на рис. 6:
Рис. 6. Варианты топологий SDN для расчёта
Таблица 3. Варианты заданий
Контрольные вопросы
1. Дайте определение сети массового обслуживания.
2. Приведите краткую классификацию сетей массового обслуживания.
3. Приведите примеры замкнутой и открытой СеМО.
4. Какими свойствами характеризуется маршрутная матрица?
5. Что гласит теорема Берке?
6. Опишите параметры открытой СеМО.
7. Опишите параметры замкнутой СеМО.
8. Определите все возможные состояния для представленной ЗСеМО, в которой находятся 3 заявки:
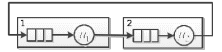
9. Определите диаграмму интенсивностей переходов для ЗСеМО, представленной выше, при условии, что в ней находятся 2 заявки.
10. Охарактеризуйте правила составления уравнений глобального баланса.
11. Какой смысл заключается в коэффициентах переходов узлов?
12. Как из диаграммы интенсивностей переходов получить уравнения равновесия вероятностных потоков?
13. Как связаны друг с другом метод уравнений глобального баланса и метод Гордона-Ньюэлла?
14. В чем заключается основное преимущество метода Бузена перед методом Гордона-Ньюэлла?
15. Кратко охарактеризуйте рекуррентное вычисление характеристик методом анализа средних значений.
16. На каких математических положениях теории массового обслуживания базируется метод MVA?
Елена Викторовна Кокорева
Программно конфигурируемые сети
Анализ эффективности
контрольная работа
Редактор: К.И. Шурыгина
Корректор:
Подписано в печать
Формат бумаги 6284 1/16, отпечатано на ризографе, шрифт №10,
Изд. л. 1,0, заказ №, тираж 10 экз.
Редакционно-издательский отдел СибГУТИ
630102, Новосибирск, ул. Кирова, 86
Для вычисления коэффициентов переходов применим ф. 13-15, при этом, чтобы получить единственное решение для замкнутой СеМО, присвоим
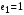 :
: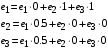
Решение системы:
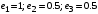 .
.Далее рекуррентно для различных значений k (количество заявок в СеМО) вычисляем с учётом начальных условий:
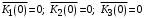 .
.– для
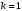
1. Среднее время реакции в узлах:
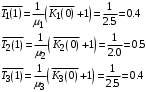 .
.2. Среднее время реакции в СеМО:
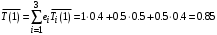 .
.3. Пропускная способность СеМО:
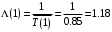 .
.4. Интенсивности потоков заявок в узлы:
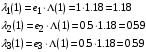 .
.5. Среднее количество заявок в узлах:
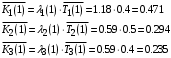 .
.– для к=К=2
1. Среднее время реакции в узлах:
 .
.2. Среднее время реакции в СеМО:
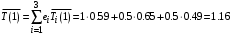 .
.3. Пропускная способность СеМО:
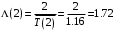 .
.4. Интенсивности потоков заявок в узлы:
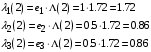 .
.5. Среднее количество заявок в узлах:
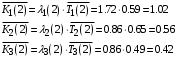 .
.По ф. (27)–(32) можно получить остальные характеристики (узловые и сетевые) моделируемой системы.
Задание
-
Вариант задания определить двумя последними цифрами пароля. Если число, образованное этими цифрами, превышает 25, то номер вариант определяется суммой двух последних цифр пароля. -
Построить модель замкнутой однородной СеМО, узлами которой являются узлы инфокоммуникационной системы, топология и параметры которой заданы в таблице 3.
П
-
Определить маршрутную матрицу, соответствующую топологии сети массового обслуживания, учитывая, что если к узлу примыкает несколько каналов, то все направления движения заявок равновероятны. -
Получить вероятностно-временные характеристики сети в зависимости от количества заявок в СеМО, узловые характеристики:
-
среднее количество заявок в узлах СеМО; -
среднее количество заявок в очередях СеМО; -
среднее время пребывания заявок в узлах СеМО; -
среднее время ожидания заявками обслуживания; -
коэффициенты загрузки узлов СеМО.
Получить вероятностно-временные характеристики сети в зависимости от количества заявок в СеМО, сетевые характеристики:
-
среднее количество заявок, ожидающих обслуживания в СеМО; -
среднее время пребывания заявок в СеМО; -
среднее время ожидания заявками обслуживания в СеМО; -
коэффициент загрузки СеМО.
Отобразить зависимости, полученные в пп. 3-4 графически.
Для расчётов использовать программные пакеты инженерной математики, такие как Mathcad, Matlab, SMathStudio (последний является бесплатно распространяемым).
Сдать контрольную работу преподавателю на проверку (отчёт в формате .doc, .docx, .pdf и обязательно файл(ы) с расчётами).
По результатам проверки внести необходимые исправления и защитить работу.
Варианты задания
Топологии сетей на рис. 6:
| 1 | 2 |
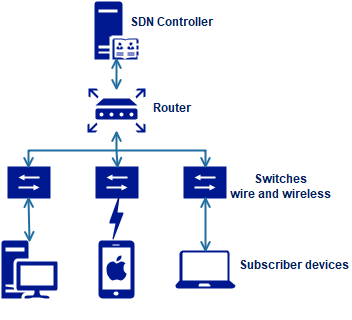 |  |
| 3 | 4 |
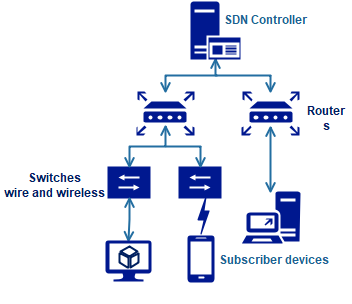 |  |
| | |
Рис. 6. Варианты топологий SDN для расчёта
Таблица 3. Варианты заданий
| № варианта | | 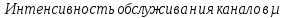 , 1/с , 1/с | |||||||
| Топология | Controller | Router | Switch | Tablet | Phone | Computer | Laptop | Monoblock | |
| 1 | 3 | 12 | 5 | 4 | 2 | 1 | 2 | 3 | 3 |
| 2 | 2 | 8 | 2 | 1 | 0.5 | 0.3 | 0.8 | 0.6 | 1 |
| 3 | 1 | 14 | 11 | 10 | 5 | 4 | 5 | 6 | 5 |
| 4 | 4 | 20 | 10 | 8 | 1 | 1 | 2 | 3 | 2 |
| 5 | 2 | 26 | 13 | 6 | 2 | 2 | 3 | 3 | 3 |
| 6 | 3 | 22 | 20 | 11 | 8 | 7 | 5 | 4 | 3 |
| 7 | 4 | 30 | 25 | 15 | 5 | 6 | 10 | 12 | 1 |
| 8 | 1 | 15 | 10 | 6 | 3 | 3 | 3 | 5 | 5 |
| 9 | 3 | 10 | 5 | 2 | 1 | 1 | 2 | 3 | 3 |
| 10 | 2 | 15 | 10 | 9 | 6 | 7 | 5 | 4 | 6 |
| 11 | 1 | 13 | 10 | 6 | 5 | 5 | 5 | 7 | 7 |
| 12 | 4 | 9 | 7 | 5 | 3 | 3 | 3 | 2 | 2 |
| 13 | 1 | 11 | 5 | 1 | 1 | 2 | 2 | 2 | 3 |
| 14 | 3 | 32 | 30 | 10 | 5 | 5 | 2 | 3 | 4 |
| 15 | 4 | 33 | 30 | 11 | 9 | 9 | 8 | 8 | 6 |
| 16 | 2 | 23 | 20 | 10 | 2 | 3 | 4 | 5 | 3 |
| 17 | 3 | 24 | 19 | 5 | 2 | 1 | 0.7 | 3 | 4 |
| 18 | 4 | 16 | 11 | 10 | 5 | 5 | 6 | 6 | 5 |
| 19 | 1 | 19 | 12 | 8 | 3 | 4 | 5 | 3 | 3 |
| 20 | 2 | 20 | 10 | 5 | 1 | 1 | 0.7 | 0.8 | 0.9 |
| 21 | 4 | 22 | 20 | 10 | 7 | 8 | 7 | 8 | 9 |
| 22 | 2 | 31 | 25 | 20 | 10 | 11 | 9 | 10 | 12 |
| 23 | 3 | 18 | 15 | 11 | 7 | 8 | 3 | 3 | 1 |
| 24 | 4 | 12 | 8 | 5 | 4 | 4 | 4 | 2 | 3 |
| 25 | 2 | 14 | 10 | 12 | 9 | 10 | 7 | 11 | 8 |
Контрольные вопросы
1. Дайте определение сети массового обслуживания.
2. Приведите краткую классификацию сетей массового обслуживания.
3. Приведите примеры замкнутой и открытой СеМО.
4. Какими свойствами характеризуется маршрутная матрица?
5. Что гласит теорема Берке?
6. Опишите параметры открытой СеМО.
7. Опишите параметры замкнутой СеМО.
8. Определите все возможные состояния для представленной ЗСеМО, в которой находятся 3 заявки:

9. Определите диаграмму интенсивностей переходов для ЗСеМО, представленной выше, при условии, что в ней находятся 2 заявки.
10. Охарактеризуйте правила составления уравнений глобального баланса.
11. Какой смысл заключается в коэффициентах переходов узлов?
12. Как из диаграммы интенсивностей переходов получить уравнения равновесия вероятностных потоков?
13. Как связаны друг с другом метод уравнений глобального баланса и метод Гордона-Ньюэлла?
14. В чем заключается основное преимущество метода Бузена перед методом Гордона-Ньюэлла?
15. Кратко охарактеризуйте рекуррентное вычисление характеристик методом анализа средних значений.
16. На каких математических положениях теории массового обслуживания базируется метод MVA?
Список литературы
-
Гольдштейн, Б. С., Елагин, В. С., Зарубин, А. А., Селиванов, А. Е. Программно-конфигурируемые сети SDN. Протокол OpenFlow [Электронный ресурс] / СПб.: СПбГУТ, 2018. — Режим доступа: http://iks.sut.ru/rubricator/programmno-konfiguriruemye-seti-sdn-protokol-openflow/ в ознакомительных целях (дата обращения: 25.08.2021). -
Кокорева, Е. В. Анализ сетей массового обслуживания [Электронный ресурс] : учебно-методическое пособие / Новосибирск : Сибирский государственный университет телекоммуникаций и информатики, 2015. — 39 c. — Режим доступа: http://www.iprbookshop.ru/55468.html по паролю. -
Вишневский, В. М. Теоретические основы проектирования компьютерных сетей // Москва: Техносфера, 2003. – 512 с. -
Клейнрок, Л. Теория массового обслуживания. – М.: Машиностроение, 1979. – 432 с. -
Башарин, Г. П., Толмачев А.Л. Теория сетей массового обслуживания и ее приложения к анализу информационно-вычислительных систем [Электронный ресурс] // Итоги науки и техники : Сер. Теор. вероятн. Мат. стат. Теор. кибернет., 21, ВИНИТИ, М., 1983, С 3–119 – Режим доступа: http://www.mathnet.ru/links/4d33dbf1daca533be0933bb49245aa72/intv56.pdf -
Кокорева Е. В. Обзор методов анализа сетей массового обслуживания для моделирования инфокоммуникационных систем // Современные проблемы телекоммуникаций : Рос. науч.-техн. конф. : материалы конф. / Сиб. гос. ун-т телекоммуникаций и информатики. Новосибирск, 2016. С. 721-730.
Елена Викторовна Кокорева
Программно конфигурируемые сети
Анализ эффективности
контрольная работа
Редактор: К.И. Шурыгина
Корректор:
Подписано в печать
Формат бумаги 6284 1/16, отпечатано на ризографе, шрифт №10,
Изд. л. 1,0, заказ №, тираж 10 экз.
Редакционно-издательский отдел СибГУТИ
630102, Новосибирск, ул. Кирова, 86