Файл: информатика.docx

Слово "информация" происходит от латинского слова informatio, что в переводе означает сведение, разъяснение, ознакомление. Понятие "информация" является базовым в курсе информатики, невозможно дать его определение через другие, более "простые" понятия. В геометрии, например, невозможно выразить содержание базовых понятий "точка", "луч", "плоскость" через более простые понятия. Содержание основных, базовых понятий в любой науке должно быть пояснено на примерах или выявлено путем их сопоставления с содержанием других понятий.

В случае с понятием "информация" проблема его определения еще более сложная, так как оно является общенаучным понятием. Данное понятие используется в различных науках (информатике, кибернетике, биологии, физике и др.), при этом в каждой науке понятие "информация" связано с различными системами понятий.

Информация в физике. В физике мерой беспорядка, хаоса для термодинамической системы является энтропия системы, тогда как информация (антиэнтропия) является мерой упорядоченности и сложности системы. По мере увеличения сложности системы величина энтропии уменьшается, и величина информации увеличивается. Процесс увеличения информации характерен для открытых, обменивающихся веществом и энергией с окружающей средой, саморазвивающихся систем живой природы (белковых молекул, организмов, популяций животных и так далее).

Таким образом, в физике информация рассматривается как антиэнтропия или энтропия с обратным знаком.

Информация в биологии. В биологии, которая изучает живую природу, понятие "информация" связывается с целесообразным поведением живых организмов. Такое поведение строится на основе получения и использования организмом информации об окружающей среде.

Понятие "информация" в биологии используется также в связи с исследованиями механизмов наследственности. Генетическая информация передается по наследству и хранится во всех клетках живых организмов. Гены представляют собой сложные молекулярные структуры, содержащие информацию о строении живых организмов. Последнее обстоятельство позволило проводить научные эксперименты по клонированию, то есть созданию точных копий организмов из одной клетки.

Информация в кибернетике. В кибернетике (науке об управлении) понятие "информация" связано с процессами управления в сложных системах (живых организмах или технических устройствах). Жизнедеятельность любого организма или нормальное функционирование технического устройства зависит от процессов управления, благодаря которым поддерживаются в необходимых пределах значения их параметров. Процессы управления включают в себя получение, хранение, преобразование и передачу информации.

---

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Наиболее употребляемыми в настоящее время позиционными системами являются:

• 1 — единичная[1] (счёт на пальцах, зарубки, узелки «на память» и др.);

• 2 — двоичная (в дискретной математике, информатике, программировании);

• 3 — троичная;

• 8 — восьмеричная;

• 10 — десятичная (используется повсеместно);

• 12 — двенадцатеричная (счёт дюжинами);

• 16 — шестнадцатеричная (используется в программировании, информатике);

• 60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания. Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия до н. э. Для обозначения чисел 0, 1, 10, 10², 10³, 104, 105, 106, 107 использовались специальные цифры. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из цифр повторялась не более девяти раз. Значение числа равно простой сумме значений цифр, участвующих в его записи. Алфавитными системами счисления пользовались древние армяне, грузины, греки (ионическая система счисления), арабы (абджадия), евреи (см. гематрия) и другие народы Ближнего Востока. В славянских богослужебных книгах греческая алфавитная система была переведена на буквы кириллицы. Еврейская система счисления в качестве цифр использует 22 буквы еврейского алфавита. Каждая буква имеет своё числовое значение от 1 до 400 (см. т. ж. Гематрия). Ноль отсутствует. Цифры, записанные таким образом, наиболее часто можно встретить в нумерации лет по иудейскому календарю.

Каноническим примером почти непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы: I обозначает 1, V — 5, X — 10, L — 50, C — 100, D — 500, M — 1000

Например, II = 1 + 1 = 2 здесь символ I обозначает 1 независимо от места в числе.

На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:

IV = 4, в то время как: VI = 6

Майя использовали 20-ричную систему счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году.Для записи основными знаками были точки (единицы) и отрезки (пятёрки).

---

Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[3], так и не числовых записей в двоичной системе кодирования[4]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[5]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[6].

Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?

Для перевода целого десятичного числа  N  в систему счисления с основанием  q  необходимо  N  разделить с остатком ("нацело") на  q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на  q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N  в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

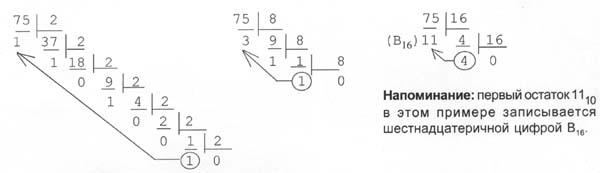
: 7510 = 1 001 0112   =  1138  =  4B16.    

Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?

Для перевода правильной десятичной дpоби  F  в систему счисления с основанием  q  необходимо  F  умножить на  q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на  q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F   в q-ичной системе. Представлением дробной части числа F   в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F  составляет k  знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2.

---

Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.

  

Как пеpевести число из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную?

Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) в виде xq = (anan-1   ...  a0  ,  a-1  a-2   ...   a-m)q   сводится к вычислению значения многочлена    x10 = an  qn +  an-1  qn-1   +   ...   +  a0   q0   +   a-1   q -1   +   a-2   q-2   +     ...     +   a-m   q-m     средствами десятичной арифметики.

Примеpы:

   

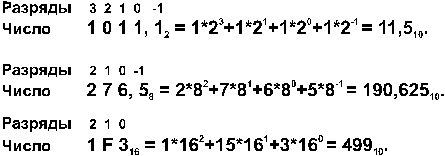
Пример 1. Сложим числа 15 и 6 в различных системах счисления.

     

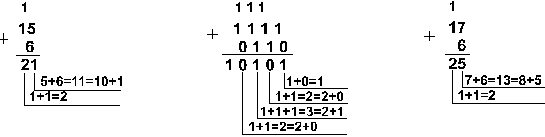
4.9. Сводная таблица переводов целых чисел из одной системы счисления в другую

Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную. Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:

Перемножим числа 115 и 51.

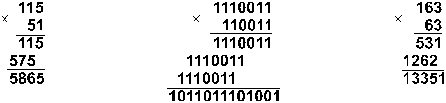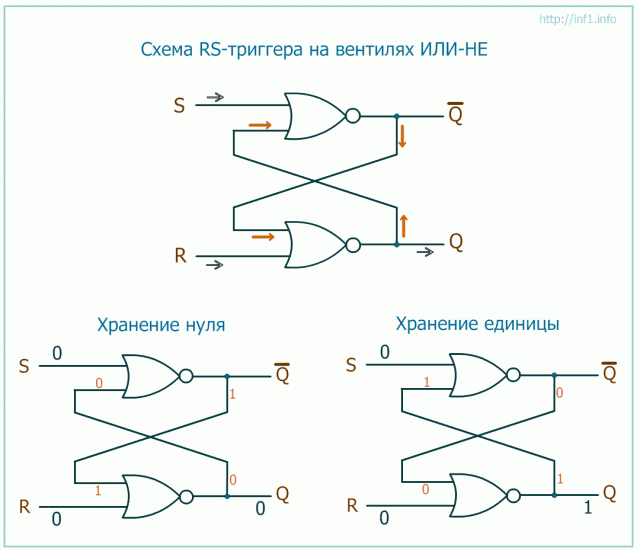
: 115 . 51 = 586510 = 10110111010012 = 133518. Проверка. Преобразуем полученные произведения к десятичному виду: 10110111010012 = 212 + 210 + 29 + 27 + 26 + 25 + 23 + 20 = 5865; 133518 = 1 . 84 + 3 . 83 + 3 . 82 + 5 . 81 + 1 . 80 = 5865. Кодирование информации — процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки.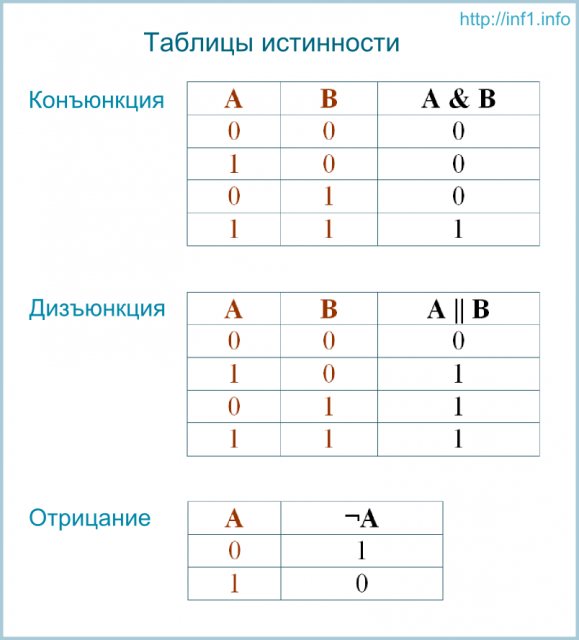

---

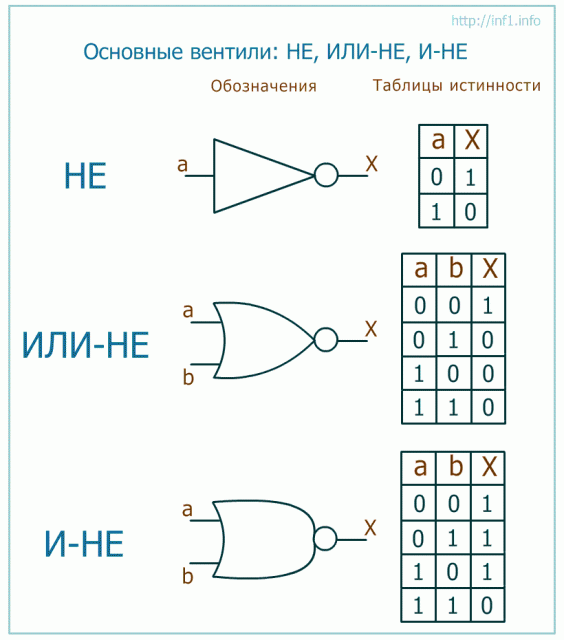
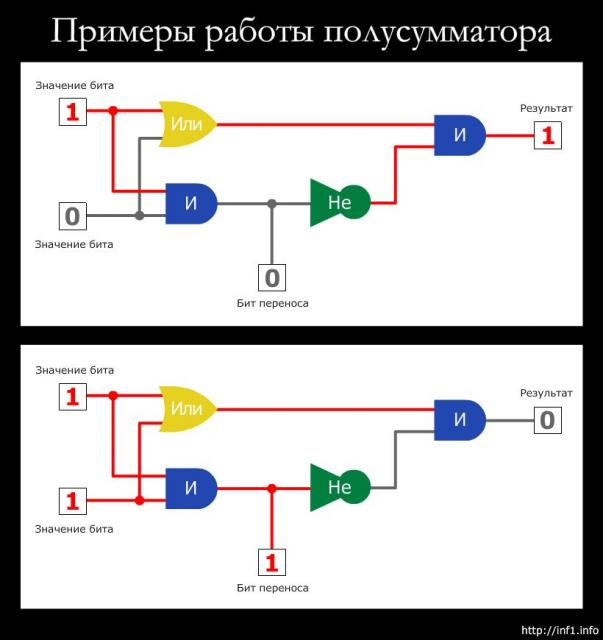
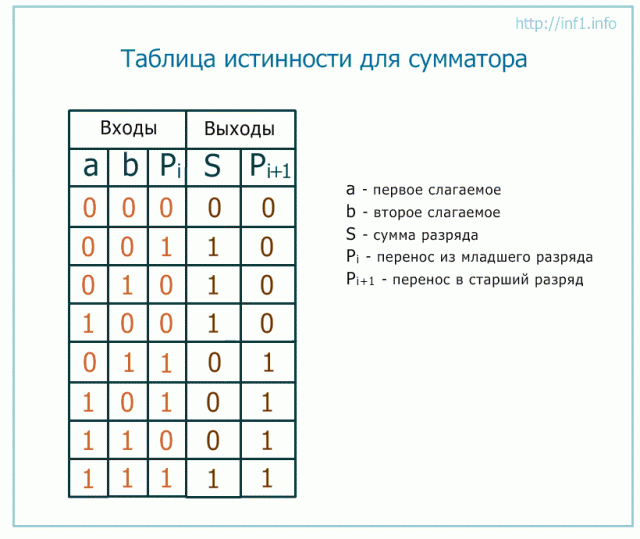
Любая конечная система попарно различимых знаков называется абстрактным алфавитом (или просто алфавитом), а все его элементы называются буквами.

Количество информации -  мера уменьшения неопределенности знаний.

Для количественного определения любой величины необходимо выбрать единицу измерения.

За единицу измерения информации принято такое количество информации, которое мы получаем при уменьшении неопределенности в два раза. Такая единица называется бит.

Существует формула, которая связывает между собой количество возможных событий N и количество информации I:

N = 2^I

По этой формуле можно определить количество возможных событий, если известно количество информации.

---