ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5269
Скачиваний: 10

81
а чтобы посчитать частично ориентированные маршруты без
звеньев надо положить
.
1
;
0
2
2
=
=
=
Θ
=
ξ
ξη
ηξ
Так, для графа на рис. 4.1.1 в первом случае имеем:
;
0
0
0
0
0
)
0
1
(
)
2
1
(
)
4
1
(
0
)
0
1
(
)
0
1
(
)
2
1
(
0
)
4
2
(
)
8
2
(
)
0
3
(
0
0
0
0
0
4
2
4
0
2
4
3
0
6
8
8
0
0
0
0
0
0
2
1
0
1
0
1
0
2
2
2
3
2
=
=
=
R
R
R
во втором:
;
0
0
0
0
0
0
4
0
0
2
0
0
0
2
2
0
0
0
0
0
0
2
0
0
0
0
2
0
0
1
2
0
0
0
0
0
0
0
2
0
0
1
0
0
0
1
1
0
3
2
=
=
=
R
R
R
в третьем:
.
0
0
0
0
0
0
4
0
0
2
0
0
0
8
10
8
0
0
0
0
0
2
0
0
0
0
2
0
0
3
4
4
0
0
0
0
0
0
2
0
0
1
0
0
0
1
1
2
3
2
=
=
=
R
R
R
Если мы интересуемся лишь наличием или отсутствием
маршрутов данной длины, а не их количеством, мы можем нало-
жить на полу кольцо К дополнительное соотношение 2=1.
Для нахождения кратчайших орцепей из вершины Х
в верши-
ну модифицируем алгоритм разметки вершин с целью учёта ориен-
тации: очередной значок получают не просто смежные с рассматри-
ваемой вершины, а лишь те, в которые из неё идут дуги.
Пусть
X
0
U
1
X
1
U
2
X
2
...X
l–1
U
l
X
l
в орграфе
L=(X,U,P)
, содержа-
щий все рёбра, называется эйлеровым путём; при Х
0
=
Х
l
имеем
эйлеровый циклический путь
.
Вводя числа
V
+
(X)=S
+
(X)+S
0
(X)
V
–
(X)=S
–
(X)+S
0
(X),
называемые соответственно полувалентностью исхода и полу-

82
валентностью захода вершины Х, можно сформулировать сле-
дующий критерий.
Теорема. Для существования эйлерова пути из вершины Х
0
в вершину Y
0
связного орграфа
L
необходимо и достаточно вы-
полнение условий
{
}
[
]
.
1
)
(
)
(
)
(
)
(
)
(
)
(
,
\
0
0
0
0
0
0
0
0
=
−
=
−
→
≠
=
∈
∀
+
−
−
+
−
+
Y
V
Y
V
X
V
X
V
Y
X
X
V
X
V
Y
X
X
X
Гамильтоновым путём (гамильтоновым орциклом) орг-
рафа L называется простой путь (простой орцикл), содержащий
все вершины L.
4.1.1 Транзитивные и квазитранзитивные графы
Граф L=(X,U,P) называется транзитивным, если
[
]
,
)
,
,
(
)
,
,
(
&
)
,
,
(
,
,
Z
X
UP
Z
V
Y
UP
Y
Y
X
UP
U
X
Z
Y
X
ω
ω
∈
∃
→
∈
∃∨
∈
∃
∈
∀
и квазитранзитивным, если
)]
,
,
(
~
)
,
,
(
&
)
,
(
[
,
,
Z
X
P
U
Z
V
Y
UP
Z
X
UP
U
X
Z
Y
X
ω
ω
∈
∃
→
∈
∃∨
∈
∃
∈
∀
.
Пример 4.1.2. Если вершины графа изображают людей, ду-
ги – иерархическое превосходство (например, старшинство), то
граф – транзитивный.
Таким образом, транзитивный граф есть частный случай
квазитранзитивного.
Из определения имеем:
− всякий подграф (не суграф!) транзитивного (квазитранзи-
тивного) графа является транзитивным (квазитранзитивным);
− если квазитранзитивный граф содержит звено или пару
противоположных дуг, то при каждой из двух вершин, инцидент-
ных этому звену (этой паре дуг), имеется хотя бы одна петля;
− если транзитивный граф содержит циклический частично
ориентированный маршрут длины
≥2, то при каждой вершине
этого маршрута есть хотя бы одна петля. Из определения подгра-
фа для доказательства второго достаточно в определении квазит-
ранзитивности положить Х=Z, последовательное применение оп-
ределения транзитивности даёт третье утверждение.
Пусть образующие полукольца подчинены условиям
83
,
1
0
;
1
2
2
=
=
=
Θ
=
=
l
ηξ
ξ
ξη
т.е. элементы матрицы смежности графа принадлежат В{0,1}.
Теорема. Пусть L=(X,U,P)– граф с упорядоченным множе-
ством вершин Х, а R
−
его матрица смежности В. Тогда необхо-
димым и достаточным условием транзитивности графа является
R=R
2
=R, а условием квазитранзитивности
− R+R
T
+R
2
=R+R
T
Доказательство. Если r
ij
=1, т.е. хоть одна дуга или звено,
соединяющие Х
i
и X
j
, а при Х
i
и X
j
– петля, то истинно
)
,
,
(
j
i
X
u
X
uP
∃
. Элемент
1
)
(
=
ij
r
r
в том и только в том случае, если
из X
i
в X
j
ведёт некоторый частично ориентированный маршрут дли-
ны 2, т.е. есть Х
К
, что истинно
)
,
,
(
&
)
,
,
(
j
K
K
i
X
V
X
vP
X
U
X
uP
∃
∃
; но
при транзитивности графа и только тогда это и только это выска-
зывание влечёт за собой истинность
)
,
,
(
Xj
Xi
P
ω
ω
∃
, т.е. равенство
r
ij
=1, какими бы не были Х
i
и X
j
. Значит, L транзитивен в том и
только в том случае, если матрица R
2
поглощается матрицей R,
т.е. если R+R
2
=R.
Аналогично доказывается второе утверждение теоремы.
4.1.2 Транзитивное замыкание
Транзитивным замыканием графа L=(X,U,P) называется
его минимальный транзитивный сверхграф, т.е. такой граф
N=(X,V,P), что
N
− есть сверхграф для L;
N
− транзитивный граф;
P
− не существует транзитивного сверхграфа N’=(X’,V’,P)
графа L, у которого
.
© V
V
u
∈
∈
Транзитивное замыкание N=(X,V,P) графа L называется
экономным, если множество V\U не содержит звеньев.
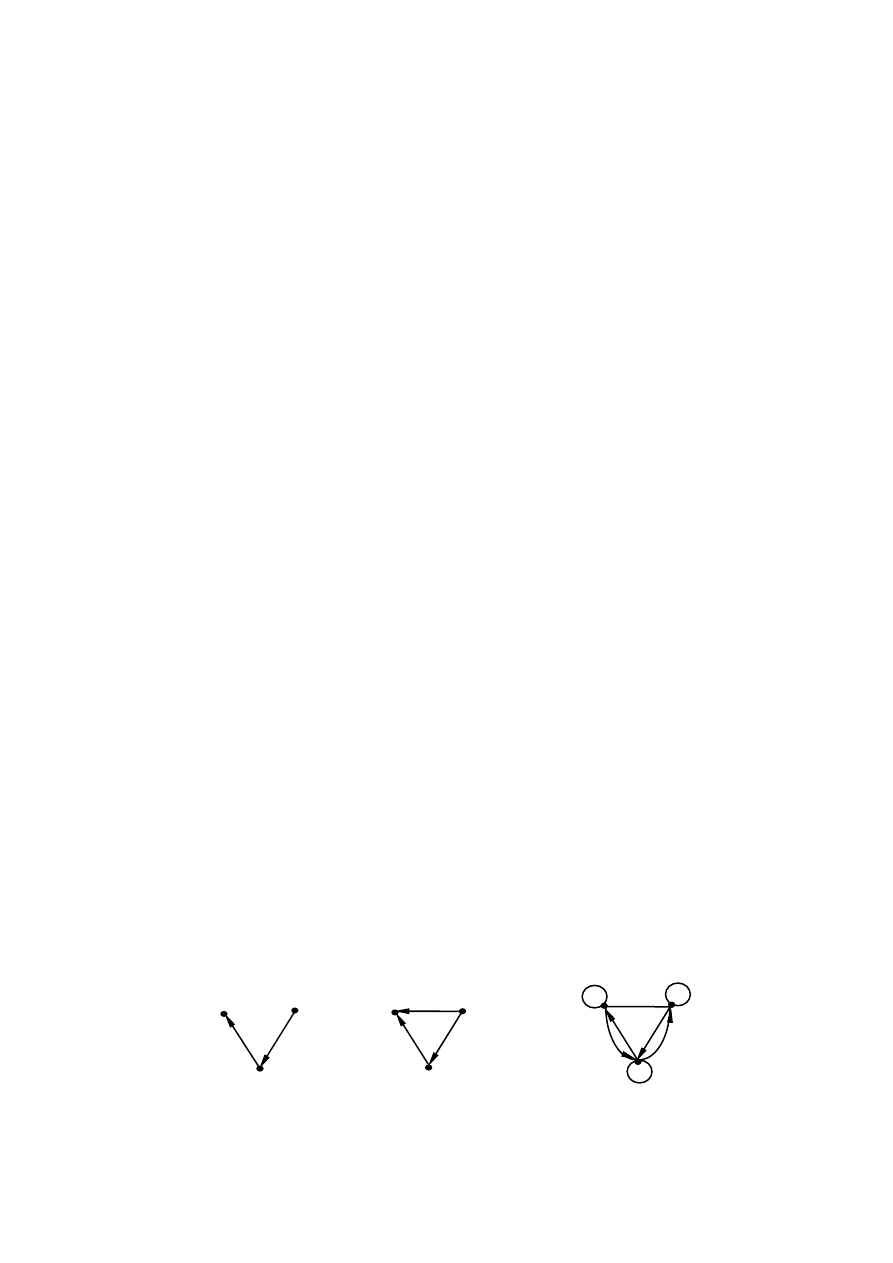
Пример 4.1.3.
L N
1
N
2
Рис. 4.1.2

84
Транзитивное замыкание N
1
графа L экономное, N
2
− не эко-
номное (перестраховка).
Теорема. Всякий граф обладает одним и только одним эко-
номным транзитивным.
Экономное транзитивное замыкание графа может быть по-
строено по его матрице смежности R на В{0,1}.
Пусть матрица смежности над В{0,1} экономного транзи-
тивного замыканий. В любом транзитивном замыкании N=(X,V,P)
вместе с каждым частично ориентированным маршрутом X
0
V
1
X
1
...
X
i–1
V
l
X
l
(S)
− должна быть дуга из X
0
B
K
l. Следовательно, матрица S
должна поглощать все степени матрицы R, т.е. поглощать сумму
R+R
2
+...+R
l+1
=R(E+R)
l
.
При некотором l
R(E+R)
lо
=R(E+R)
lo+1
и эта матрица транзитивная и можно
S=R(E+R)
lо
.
Следствиями из доказанной теоремы полагаются следующие
утверждения
− в классе всех неориентированных униграфов каж-
дый граф обладает единственным транзитивным замыканием.
4.2
Бикомпоненты
графа
Говорят, что в орграфе L=(X,U,P) вершина Y достижима из
вершины Х, если существует путь из Х в Y. Высказывание «Y дос-
тижима из X в L» будет обозначать Д(X,Y).
Вершины Х и Y в L взаимодостаточны, если истинно
Д(X,Y)& Д(Y,X). Отношение взаимодостижимости рефлексивно,
симметрично и транзитивно, поэтому множество Х разбивается
на попарно непересекающиеся подмножества взаимодостижимых
вершин подграфа. Порождаемые этим подмножеством называют-
ся компонентами бисвязности (бикомпонентами). И их количест-
во обозначается через
)
(L
χ
. При
)
(L
χ
=1 граф называется бисвяз-
ным.
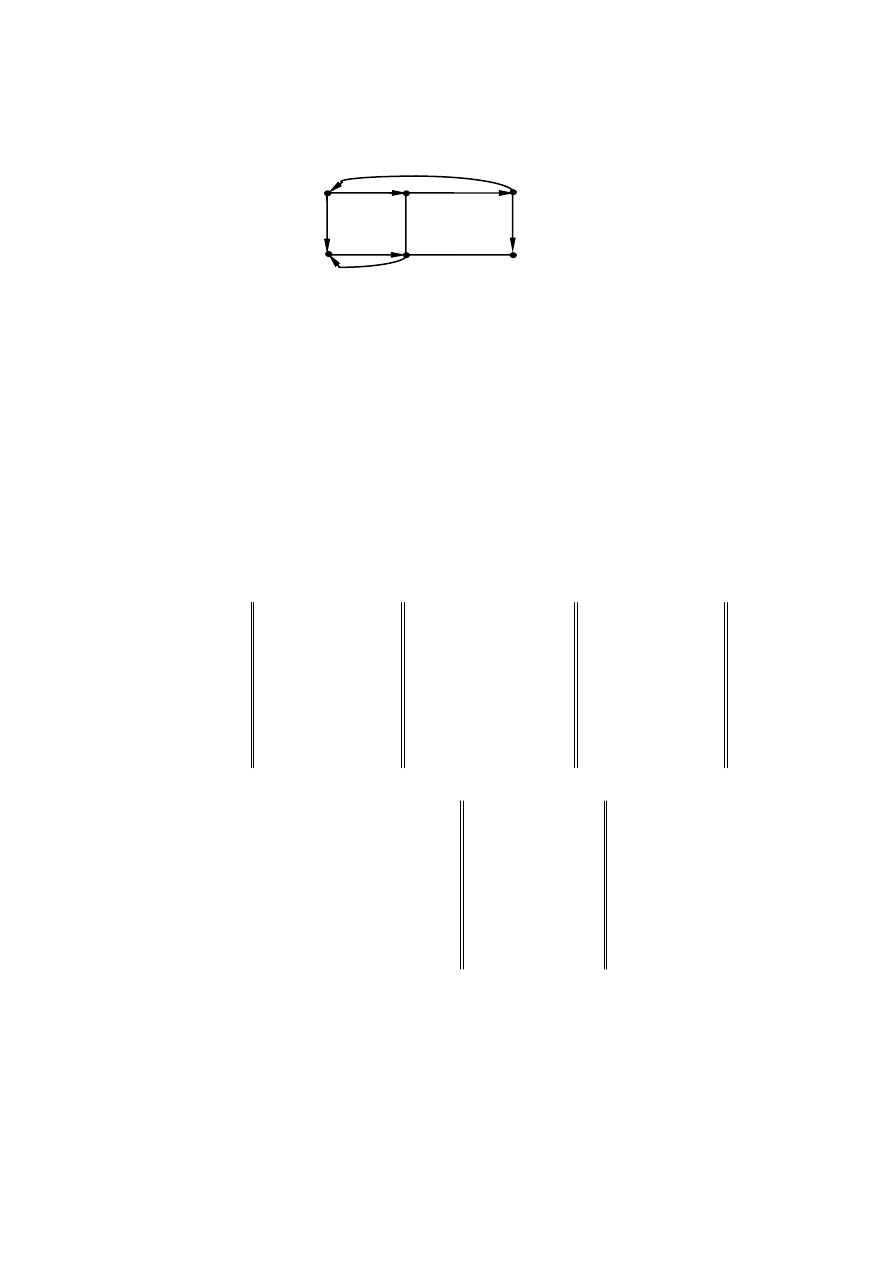
Пример 4.2.1. Граф на рисунке 4.2.1. имеет три компоненты
бисвязности – они порождаются множествами вершин {a,b,c},
85
{d,l},{f}. Если направление дуги изменить на противоположное,
то граф станет бисвязным.
Пусть граф задан матрицей смежности R над B{0,1}. Эле-
мент матрицы S
ij
(l)
матрицы (E+R)
2
равен 1 тогда и только тогда,
когда из i-ой вершины графа в в j-вершину существует путь дли-
ны не более l. Существует также l, что (E+R)
lo
=(E+R)
lo+
, причём
S
ij
(lо)
равен 1 в том и только в том случае, если j - ая вершина дос-
тижима из i-ой. Тогда каждая бикомпонента состоит из тех вер-
шин, которым в матрице (E+R)
lo
отвечают одинаковые строки.
Пример 4.2.2. Для графа на рис. 4.2.1 имеем
1
0
0
0
0
0
1
1
1
0
0
0
1
1
1
0
0
0
1
0
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
)
(
1
0
0
0
0
0
1
1
1
0
0
0
0
1
1
0
0
0
1
0
0
1
0
1
0
1
0
1
1
0
0
0
1
0
1
1
2
=
+
=
+
R
E
R
E
1
1
1
0
0
0
1
1
1
0
0
0
1
1
1
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
)
(
)
(
4
3
=
+
=
+
R
E
R
E
Теорема Камьона
−
Фаулькса. Полный обыкновенный орг-
раф обладает гамильтоновым циклом тогда и только тогда, когда
он бисвязен.
Теорема Редеи. Всякий плотный орграф имеет хотя бы один
гамильтонов путь.
a
d
f
l
a
c
b
f
c
Рис. 4.2.1