ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6222
Скачиваний: 28

16
1.4
Экстремальные
элементы
множеств
В соответствии с отношением порядка говорят, что при x
1
≤ x
2
элемент x
1
предшествует элементу
x
2
или x
2
следует за
x
1
.
Пусть имеется подмножество X
′ ⊂ X, где X упорядоченное
множество, т.е. множество, для элементов которого определено от-
ношение порядка. Тогда мажорантой множества X
′ называется эле-
мент x
max
∈ X, следующий за всеми элементами множества X′,
x
max
≥x (x
max
∈ X). При этом мажоранта может и не принадлежать
множеству X
′. Если же x
max
∈ X′, то x
max
называется наибольшим
элементом, или максимумом множества X
′.
Минорантой множества X
′ называется элемент x
min
∈ X, пред-
шествующий всем элементам множества X
′. Если элемент x
min
∈
X
′, то он называется наименьшим элементом, или минимумом
множества X
′.
1.5
Отображения
множеств
Пусть X и Y - два непустых множества. Закон G, согласно ко-
торому любому элементу x
∈ X ставится в соответствие элемент
y
∈ Y, называется однозначным отображением X в Y, или функци-
ей, определенной на X и принимающей значения на Y.
Используются следующие формы записи:
G: X
→ Y или y = G(x), x ∈ X, y ∈ Y.
В случае однозначного отображения элемент y = G(x) называ-
ется образом элемента x.
Возможна ситуация, когда каждому x
∈ X отображение G ста-
вит в соответствие некоторое подмножество G(x)
⊂ Y. Тогда обра-
зом элемента x будет подмножество G(x), а отображение G, будет
называться многозначным отображением. Отображение является,
таким образом, всюду определенным соответствием, т.е. частным
случаем соответствия и определяется тройкой множеств (X, Y, G).
Интересным является случай, когда множества X и Y совпада-
ют. При этом отображение G: X
→ X представляет собой отображе-
ние множества X самого в себя и определяется парой (X, G), где
G
⊂ X × X. Подробным изучением таких отображений занимается
теория графов. Коснемся лишь нескольких операций над ними.
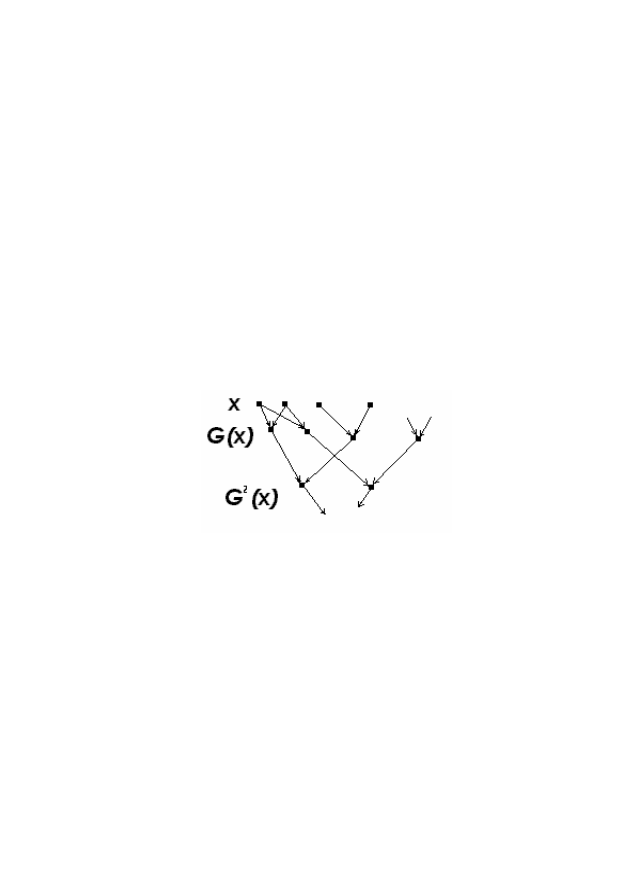
17
Пусть G и H – отображения множества X в X. Композицией
этих отображений назовем отображение GH, которое определяется
следующим образом: GH(x) = G(H(x)).
В частном случае при H = G получим отображения
G
2
(x) = G(G(x)), G
3
(x) = G(G
2
(x)) и т.д.
Для произвольного S
≥ 2: G
S
(x) = G(G
S-1
(x)).
Введем для общности рассуждений соотношение G
0
(x) = x. То-
гда можно записать: G
0
(x) = G(G
-1
(x)) = GG
-1
(x) = x.
Это означает, что G
-1
(x) представляет собой обратное отобра-
жение. Тогда G
-2
(x) = G
-1
(G
-1
(x)) и т.д.
Пусть, например, X - множество людей. Для каждого человека
x
∈ X обозначим через G(x) множество его детей. Тогда G
2
(x) -
множество внуков x, G
3
(x) - множество правнуков x, G
-1
(x) - множе-
ство родителей x и т.д. Изображая людей точками и рисуя стрелки,
идущие из x в G(x), получим родословное, или генеалогическое де-
рево (рис. 1.7.)
Рис. 1.7 – Генеалогическое дерево
1.6
Задачи
и
упражнения
1.
Даны множества X = {1, 2, 3, 4, 5}, Y = {2, 4, 6, 7}, найдите
X
∪ Y, X ∩Y, X \ Y, Y \ X.
2.
Пусть X
− множество отличников в группе, Y − множество сту-
дентов группы, проживающих в общежитии. Найдите множества:
X
∪ Y, X ∩ Y, X \ Y, Y \ X.
3.
Что представляет собой пересечение множества всех прямо-
угольников с множеством всех ромбов?
4.
Пусть I = {x
1
, x
2
, x
3
}
− универсальное множество, а X = {x
1
, x
2
},
Y = {x
2
, x
3
}, Z = {x
3
}
− его подмножества. Определите перечис-
18
лением множества: X
× X, Z × Z, X × Y, Y × X, X × Y ∩ Y × X,
X
× Y ∪ Y × X.
5.
Проиллюстрируйте графически тождества
X
∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z),
X
∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z).
6.
Пусть R
− множество вещественных чисел, X = {x ∈ R /
0
≤ x ≤ 1}, Y = {y ∈ R / 0 ≤ y ≤ 2}. Что представляют собой мно-
жества X
∪ Y, X ∩ Y, X \ Y?
7.
Начертите фигуры, изображающие множества A = {(x, y)
∈ R
2
/
x
2
+ y
2
≤ 1}, B = {(x, y) ∈ R
2
/ x
2
+ (y-1)
2
≤ 1}, где R
2
− вещест-
венная плоскость. Какие фигуры изображают множества A
∪ B,
A
∩ B, R
2
\ A?
8.
Пусть X, Y, Z
− подмножества множества R
2
, равные:
X = {(x, y)
∈ R
2
/ x
≥ 0}, Y = {(x, y) ∈ R
2
/ y
≥ 0}, Z = {(x, y) ∈ R
2
/
x + y
≥ 1}. Представьте геометрически множества
,
,
,
Z
Y
X
∪
,
Y
X
,
∪
Y
X
∩
,
Y
X
,
∩
Y
X
∩
,
Z
X
,
∩
Z
X
∩ ∩
,
Z
Y
X
.
∩ ∩
Z
Y
X
9.
Пусть X = {-1, -2, -3, 1, 2, 3, 0} и Y
− множество всех натураль-
ных чисел. Каждому числу x
∈ X ставится в соответствие его
квадрат. Выпишите все пары, принадлежащие этому соответст-
вию.
10.
Пусть X = {«атом», «стол», «море», «мера»}, Y = {а, м, о, р, е}.
Составьте декартово произведение X
× Y. Отметьте в нем пары,
связанные соответствием «в слово x входит буква y».
11.
Пусть V
− множество положительных целых чисел от 1 до 20, на
котором задано отношение R: «число x делится на число y», при-
чем x
∈ V, y ∈ V. Выпишите все пары из V, находящиеся в от-
ношении R.
12.
Дано множество B = {1, 3, 5, 7, 9}. Элементы этого множества
связаны отношением S: «число x на 2 больше числа y». Запишите
множество пар, принадлежащих этому отношению.
13.
Определите свойства следующих отношений:
а) «прямая x пересекает прямую y» (на множестве прямых);
б) «число x больше числа y на 2» (на множестве натуральных
чисел);

19
в) «число x делится на число y без остатка» (на множестве на-
туральных чисел);
г) «x
− сестра y» (на множестве людей).
14.
На множестве X = {x / x
∈ N, x < 12} задано отношение R: «x и y
имеют один и тот же остаток при делении на 5» (x
∈ X, y ∈ X).
Покажите, что R
− отношение эквивалентности. Запишите все
классы эквивалентности, на которые разбивается множество
данным отношением.
15.
Рассмотрите на множестве людей следующие отношения, укажи-
те среди них отношения эквивалентности:
а) «x похож на y»;
б) «x и y живут в одном доме»;
в) «x и y
− друзья»;
г) «x живет этажом выше, чем y».
16.
Отношение S на множестве X = {1, 2, 3} состоит из пар: (1, 2),
(1, 1), (2, 2), (2, 1), (3, 1), (3, 3). Является ли S отношением экви-
валентности на множестве X?
17.
Какие из нижеперечисленных отношений являются отношениями
квазипорядка, порядка, строгого порядка?
а) «отрезок x длиннее отрезка y»;
б) «отрезок x короче отрезка y в 2 раза»
− на множестве отрез-
ков;
в) «x старше по возрасту, чем y»;
г) «x является сестрой y»;
д) «x живет в одном доме с y»;
е) «x
− друг y» − на множестве людей;
ж) «число x не меньше числа y»
− на множестве R;
з) «окружность x лежит внутри окружности y»
− на множестве
окружностей плоскости.
18.
Докажите тождества: A
∩ (B \ A) = ∅, A \ (B ∪ C) = (A \ B) \ C.
19.
Решите систему уравнений
A \ X = B,
A
∪ X = C,
где A, B, C - заданные множества и B
⊂ A ⊂ C.
20.
Докажите, что A = B
⇔ (A \ B) ∪ (B \ A) = ∅.
21.
Докажите, что если отношения R
1
и R
2
рефлексивны, то рефлек-
сивны и отношения R
1
∪ R
2
, R
1
∩ R
2
.

20
22.
Докажите, что если отношения R
1
и R
2
симметричны, то симмет-
ричны и отношения R
1
∪ R
2
, R
1
∩ R
2
.
23.
Докажите, что два множества равны тогда и только тогда, когда
результаты их пересечения и объединения совпадают.
24.
Известно, что из 100 студентов живописью увлекается 28, спор-
том
− 42, музыкой − 30, живописью и спортом − 10, живописью
и музыкой
− 8, спортом и музыкой − 5, живописью, спортом и
музыкой
− 3. Определите количество студентов:
а) увлекающихся только спортом;
б) ничем не увлекающихся.
2
ОСНОВЫ
ТЕОРИИ
ГРАФОВ
На практике часто бывает полезно изобразить некоторую си-
туацию в виде рисунков, составленных из точек (вершин), представ-
ляющих основные ситуации, и линий (ребер), соединяющих опреде-
ленные пары этих вершин и представляющих связи между ними.
Таким способом удобно представлять структуру системы (вершины
– блоки, ребра – связи между блоками). Удобны графы при исследо-
вании систем методом пространства состояний. В этом случае вер-
шины – состояния системы, процесса, ребра – действия, которые
могут изменить состояние. При решении оптимизационных задач
вершинами могут быть предполагаемые решения, ребрами – прави-
ла для их нахождения.
Такие рисунки известны под общим названием графов. Графы
встречаются в разных областях под разными названиями: “структу-
ры” в гражд-анском строительстве, “сети” в электротехнике, “социо-
граммы” в социологии и экономике, “молекулярные структуры” в
химии, и т. д.
Начало теории графов как математической дисциплины было
положено Эйлером в знаменитом рассуждении о Кенигсбергских
мостах. Однако эта статья, написанная в1736 г, была единственной в
течение почти ста лет. Интерес к этой науке возродился около сере-
дины ХIХ в. в связи с развитием естественных наук (исследования
электрических сетей, моделей кристаллов и структур молекул),
формальной логики (бинарные отношения можно изучать в форме
графов). Кроме того, оказалось, что многие математические голово-
ломки могут быть сформулированы в терминах теории графов. Это