ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5079
Скачиваний: 26

76
пользует исходный массив
A
. Это важно, так как «внутренние»
свойства этого массива существенно влияют на сложность решения
задачи.
Модель 2 описана в терминах выборок ограниченной дли-
ны из конечного множества элементов. Выборки наряду с чисто
комбинаторным (перестановки, сочетания, размещения и т.д.) могут
иметь и другие представления. Основные из них используют терми-
нологию теории графов и булевой алгебры.
Каждое из таких описаний имеет свои преимущества: комби-
наторное ближе к практической постановке задачи; графовое обла-
дает большей наглядностью, булевое является универсальным (лю-
бая задача комбинаторного программирования может быть описана
в булевых переменных).
Рассмотрим возможности различных представлений на при-
мере задачи о назначениях. Ранее мы дали чисто комбинаторное
описание этой задачи. На множестве
N
Π
минимизировать
функцию
∑
∈
=
M
I
j
j
j
t
F
).
,
(
)
(
3
π
π
Дадим графовое описание задачи. Для этого нам потребуют-
ся некоторые дополнительные понятия теории графов.
Граф
)
( X
G
называется двудольным, если множество
X
его вершин можно разбить на два таких подмножества
X ′
и
X ′′
,
что для имеющихся в графе дуг все начальные вершины входят в
X ′
, а все конечные – в
X ′′
. Двудольный граф называется полным,
если любая вершина
X
x
′
∈
′
соединена дугой с любой вершиной
X
x
′′
∈
′′
.
)
,
(
N
N
G
′′
′
- полный двудольный граф, в котором
N ′
-
количество вершин в
X ′
и
N ′′
- количество вершин в
X ′′
.
В графе
)
( X
G
n
-паросочетанием называется совокуп-
ность из
n
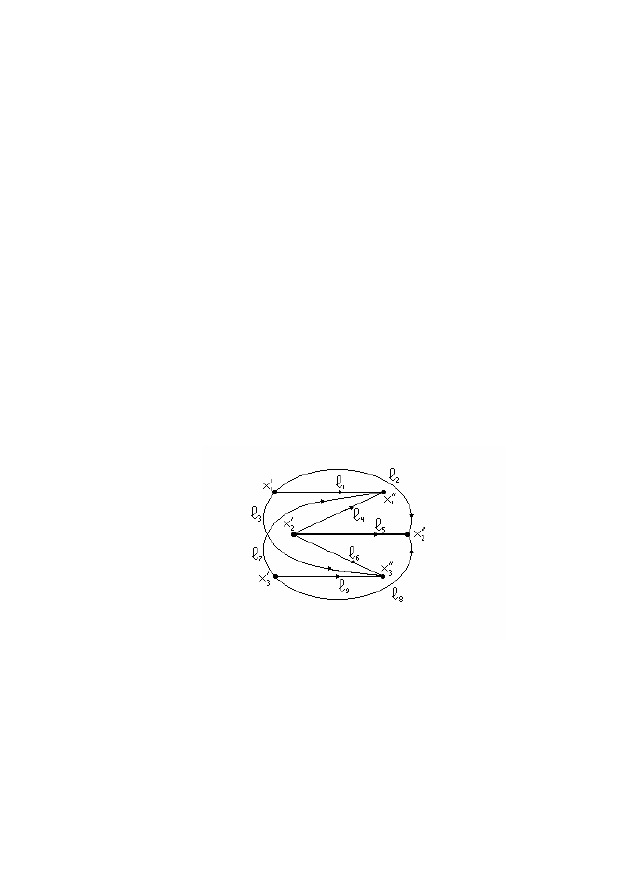
несмежных дуг. В графе на рис. 3.2 имеется 6 различных
3 – паросочетаний:
).
,
,
(
),
,
,
(
),
,
,
(
),
,
,
(
),
,
,
(
),
,
,
(
7
5
3
8
4
3
7
6
2
9
4
2
8
6
1
9
5
1
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
Пусть граф
G
является взвешенным по дугам. Тогда вес лю-
77
бого паросочетания равен сумме весов дуг, входящих в него. С уче-
том этих определений можно дать следующую постановку задачи в
терминах теории графов.
Во взвешенном двудольном графе
),
,
(
N
N
G
дугам кото-
рого
)
,
(
''
'
j
i
x
x
приписаны веса
),
,
( j
i
c
найти
N
- паросочетание
максимального (минимального) веса.
Если в графе
)
3
,
3
(
G
(рис. 3.2) задать веса дуг матрицей
,
3
1
3
1
2
4
2
3
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
C
то максимальным в нем будет паросочетание
).
,
,
(
9
4
2
l
l
l
Можно показать, что между
N
- паросочетаниями графа
)
,
(
N
N
G
и перестановками
π
из
N
Π
существует взаимоод-
нозначное соответствие. Оно осуществляется следующим образом:
если в паросочетание входит дуга
)
,
(
''
'
j
i
x
x
, то в соответствующей
перестановке
.
i
j
=
π
При таком соответствии значение функции
)
(
3
π
F
и вес соответствующего паросочетания совпадают.
Рассмотрим булевое описание задачи о назначениях. Поста-
вим в соответствие каждой перестановке
N
Π
∈
π
набор из
2
N
Рис. 3.2 – Пример двудольного графа

78
булевых переменных
.
ij
y
Соответствие заключается в следующем:
⎩
⎨
⎧
=
=
.
,
0
1
случае
противном
j
i
в
при
y
ij
π
При фиксированном
i
i
′
=
ровно одна из переменных
j
i
y
,
′
отлична от нуля, а при фиксированном
j
j
′
=
ровно одна из пере-
менных
j
i
y
′
отлична от нуля, т.е. наборы булевых переменных
ij
y
, соответствующие перестановкам
π
из
N
Π
, должны удовле-
творять соотношениям:
∑
∑
∈
∈
=
=
N
N
I
i
I
j
ij
ij
y
y
.
1
,
1
(15)
Справедливо и обратное. По любому решению в булевых пе-
ременных системы (15) можно построить соответствующую ему
перестановку. Например, для
3
=
N
набору переменных
ij
y
.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
0
1
0
1
0
]
[
ij
y
соответствует перестановка
).
3
,
1
,
2
(
=
′
π
Целевая функция задачи назначения для любого набора буле-
вых переменных
]
[
ij
y
, удовлетворяющих соотношениям (15), мо-
жет быть представлена так:
∑
∑
∈
∈
=
N
N
I
j
ij
I
i
ij
y
j
i
c
y
F
.
)
,
(
])
([
1
(16)
Таким образом, получим следующее булевое описание задачи
о назначениях:
На множестве наборов булевых переменных
]
[
ij
y
мак-
симизировать (минимизировать) функцию (16) при ограниче-
ниях (15).
Мы рассмотрели различные способы описания задач комби-

79
наторного программирования. Возможность использования описа-
ний различного типа – характерное свойство задач комбинаторного
программирования. При этом в общем случае ни один способ опи-
сания не имеет явного преимущества перед другими. Выбор способа
определяется удобством представления и исследования задачи. В
свою очередь, способ описания существенно влияет на выбор мето-
да решения задачи комбинаторного программирования.
Из представленных способов описания задач комбинатор-
ного программирования важными особенностями выделяется буле-
вое описание. Первой особенностью является сравнительная про-
стота его получения для большинства задач комбинаторного про-
граммирования независимо от их исходной формулировки. Вторая
особенность состоит в том, что любая задача в булевых переменных
может быть приведена к линейному виду, что позволяет использо-
вать для ее решения методы линейного программирования.
Рассмотрим такое преобразование. Пусть имеется задача: на
множестве
N
B
всех булевых векторов
)
,...,
,
(
2
1
N
y
y
y
y
=
макси-
мизировать функцию
)
(
0
y
f
при ограничениях
)
(
0
)
(
M
i
I
i
y
f
∈
≤
.
Предлагаемое преобразование содержит два перехода:
1) функции
)
)(
(
M
i
I
i
y
f
∈
заменяются полиномами (кстати,
такие функции от булевых переменных, которые принимают произ-
вольные действительные значения, называются псевдобулевыми);
2) каждое произведение булевых переменных заменяется но-
вой булевой переменной и двумя ограниченными.
В основе первого перехода лежит возможность представления
любой псевдобулевой функции
)
,...,
,
(
2
1
m
y
y
y
ϕ
в виде
)].
,...,
,
,
0
(
)
,...,
,
,
1
(
[
)
,...,
,
,
0
(
)
,...,
,
(
3
2
3
2
1
3
2
2
1
m
m
m
m
y
y
y
y
y
y
y
y
y
y
y
y
y
ϕ
ϕ
ϕ
ϕ
−
+
=
Последовательное использование соотношения позволяет
любую функцию
ϕ
представить в виде полинома.
Второй переход состоит в линеаризации этого полинома. Для
примера рассмотрим произведение первых
k
переменных:

80
k
y
y
y
2
1
⋅
. Введем новую переменную
k
y
y
y
y
2
1
0
⋅
=
(17)
Очевидно, что
0
y
- булевая переменная. Представление (17)
для нее может быть заменено двумя линейными неравенствами
.
1
...
,
0
...
0
2
1
0
2
1
−
≤
−
+
+
+
≥
−
+
+
+
k
y
y
y
y
ky
y
y
y
k
k
Первое из них обеспечивает равенство
0
y
нулю, если хотя бы
одна из переменных
)
,...,
2
,
1
(
k
i
y
i
=
равна 0. Второе обеспечивает
равенство
1
0
=
y
при всех
).
,...,
1
(
1
k
i
y
i
=
=
Таким образом, произведение булевых переменных всегда
может быть заменено новой переменной и двумя линейными огра-
ничениями. Такое представление позволяет использовать для реше-
ний задачи методы линейного программирования, т.к. задача нахо-
ждения экстремума линейной формы при линейных ограничениях и
есть задача линейного программирования (ЛП). Многие экстре-
мальные задачи комбинаторного программирования сводятся к за-
дачам линейного программирования, отличаясь лишь дополнитель-
ным условием целочисленности аргументов. Среди них важным
подклассом являются задачи булевого линейного программирования
(только что рассмотренные).
Можно сказать, что задача ЛП представляет собой типичный
пример комбинаторной задачи (даже без добавления условия цело-
численности переменных, т.к. оптимальным решением задачи ЛП
является одна из вершин многогранника, определяемого системой
ограничений (неравенств), а любая вершина однозначно определяет-
ся как сочетание из
M
N
+
элементов по
N
(
N
– число пере-
менных,
M
– число ограничений).
Тем не менее, вряд ли целесообразно включать ЛП в комби-
наторное, поскольку первое представляет собой специфическую и
хорошо разработанную ветвь математического программирования.