Вопросы

1. 
   Задача, приводящая к понятию дифференциального уравнения.
   
2. 
   Основные понятия о дифференциальных уравнениях
   
3. 
   Геометрическое истолкование задачи отыскания решения обыкновенного дифференциального уравнения первого порядка, разрешенного относительно производной. Поле направлений. Интегральные кривые.
   
4. 
   Постановка задачи Коши для обыкновенного дифференциального уравнения.
   
5. 
   Дифференциальные уравнения первого порядка с разделенными переменными.
   
6. 
   Дифференциальные уравнения первого порядка с разделяющимися переменными.
   
7. 
   Однородные дифференциальные уравнения первого порядка.
   
8. 
   Уравнения, приводящиеся к однородным.
   
9. 
   Линейные дифференциальные уравнения первого порядка.
   
10. 
    Уравнения Бернулли.
    
11. 
    Дифференциальные уравнения в полных дифференциалах.
    
12. 
    Интегрирующий множитель.
    
13. 
    Дифференциальные уравнения высших порядков, допускающие понижение порядка.
    
14. 
    Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
    
15. 
    Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
    
16. 
    Задачи Коши и краевая задача для дифференциального уравнения n-го порядка.
    

Билет 1. Задача, приводящая к диф.уравнениям

Многие задачи естествознания приводят к нахождению неизвестных функций, описывающих рассматриваемые явления или процессы, когда известны соотношения, связывающие между собой эти функции и их производные. Такие соотношения называются дифференциальными уравнениями. В качестве иллюстрации рассмотрим следующие примеры.

 Допустим, что в каждый момент времени t известна скорость точки, движущейся по оси Ox , где f (t) – функция, непрерывная на

Кроме того, будем считать, что известна абсцисса x0 этой точки в некоторый определённый момент времени t = t0 . Требуется найти закон

движения точки, то есть зависимость абсциссы движущейся точки от времени.

Решение. Положение точки определяется одной координатой x и задача состоит в том, чтобы выразить 

---

x как функцию от t . Принимая во внимание механический смысл первой производной, мы получим равенство



Как известно из интегрального исчисления



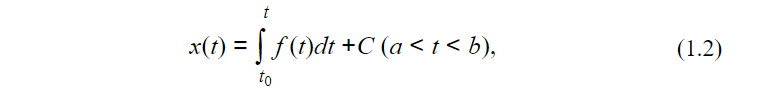
где верхний предел интеграла – переменный, нижний t0 есть некоторое фиксированное число из (a,b) , C – произвольная постоянная. Так как в

формулу (1.2) входит произвольная постоянная, то мы ещё не получили определённого закона движения точки.

Выделим из множества движений (1.2) то движение, при котором движущаяся точка занимает заданное положение x0 в заданный момент

времени t0 :

t0

x0 = ∫ f (t)dt +C С = x0 ,

t0

что вместе с (1.2) даёт искомый закон движения точки:

t

x(t) = ∫ f (t)dt + x0 (a < t < b) .

t0

Билет 2. Основные понятия о диф. Уравнениях



Билет 3. Геометрическое истолкование задачи отыскания решения обыкновенного дифференциального уравнения первого порядка, разрешенного относительно производной. Поле направлений. Интегральные кривые.


По́ле направле́ний — геометрическая интерпретация множества линейных элементов, соответствующих системе обыкновенных дифференциальных уравнений.

Любая интегральная кривая системы обыкновенных дифференциальных уравнений в каждой своей точке касается отвечающего этой точке направления поля, и любая кривая, обладающая этим свойством, является интегральной кривой системы.

---

Интегральная кривая - это график решения дифференциального уравнения.

 Кривой данный график называется, так как он изображает функцию от скалярной пер-менной.

Билет 4. Постановка задачи коши для обыкновенного дифференциального уравнения

Билет 5. Диф. Уравнения первого порядка с разделенными переменными



Билет 6. Диф. Уравнения первого порядка с разделяющимися переменными



Билет 7. Однородные дифференциальные уравнения первого порядка.



Билет 8. Уравнения, приводящиеся к однородным








Билет 9. Линейные ДУ первого порядка





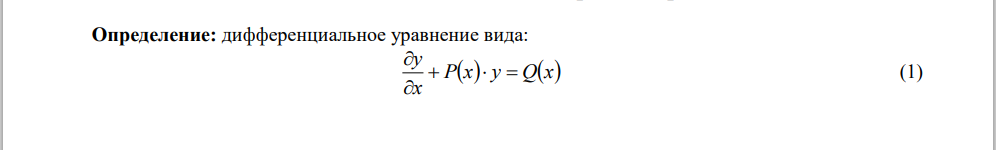
Билет 10. Уравнение Бернулли.



Билет 11. ДУ в полных дифференциалах.





Билет 12. Интегрирующий множитель

---

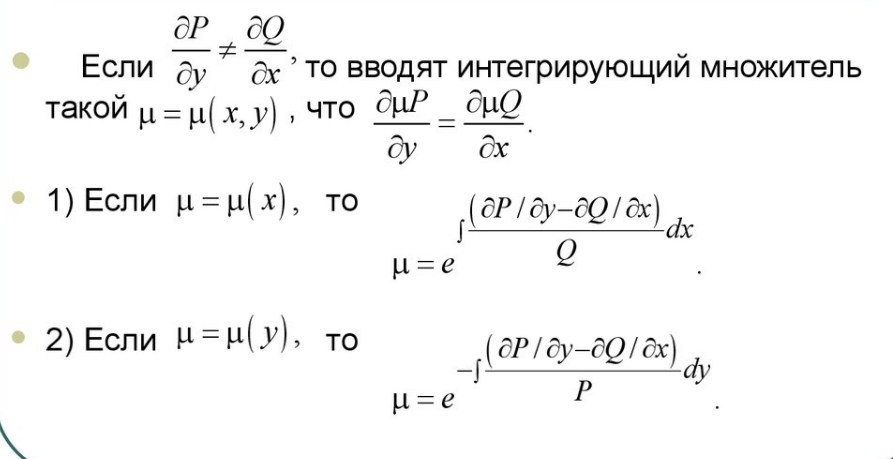
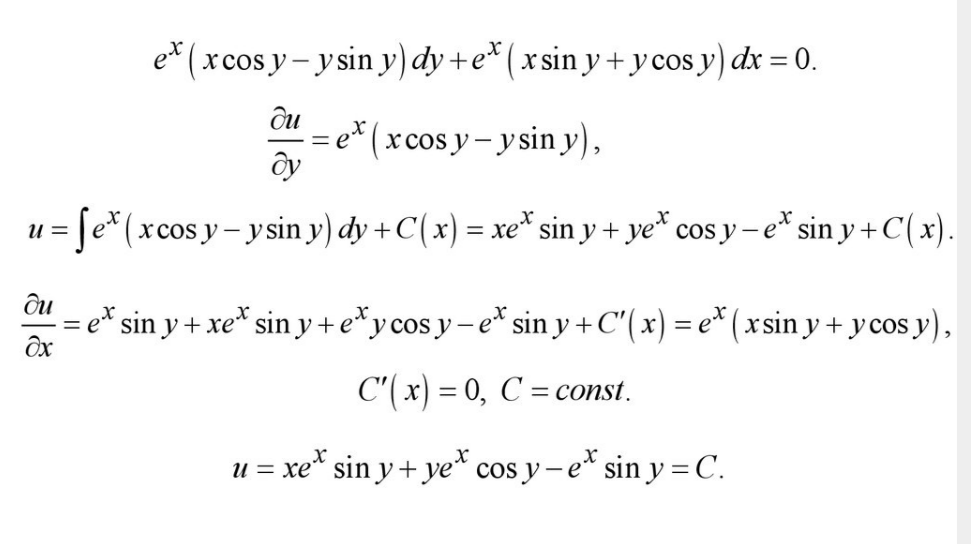
Билет 13. ДУ высших порядков, допускающие понижение порядка.









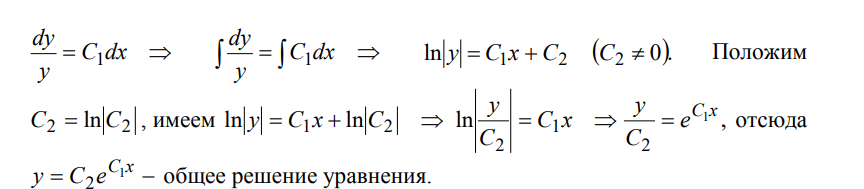
Билет 14. Линейные однородные ДУ второго порядка с постоянными коэффициентами





Билет 15. . Линейные неоднородные ДУ второго порядка с постоянными коэффициентами






Билет 16. Задача Коши и краевая задача для ДУ n-го порядка.

Задача Коши:





Краевая задача:

---

Смотрите также файлы

• Вирусы.pptx

• Протокол гэк Председатель гэк 20 г. Допущена к защите.doc

• Группа Отчет подготовил фио проверил преподаватель.pptx

• Аттестация по результатам практики.docx

• С. А. Зайцев 26 мая 2023 г.docx